
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
K — коэффициент трения скольжения,Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
N — сила нормальной реакции опоры Законы трения: 1) При стремлении сдвинуть одно тело по поревхности другого возникает сила трения или сила сцепления которая может принимать любые значения от 0 до Приложенная к телу сила трания направлена в сторону противоположную той куда действующая на тело сила стремится его сдвинуть. 2) Предельная сила трения численно равна произведению статическому коэффициенту трения на нормальное давление или нормальную реакцию. Cтатический коэффициент трения определяется опытным путём и зависит от материала соприкосновения тел и состояния поверхностей. Значения предельной сили трения в довольно широких пределах не зависит от размеров соприкасающихся предметов. Из первых двух законов следует, что при равновесии Значение силы трения при покое определяется неравенством (1) и следовательно это значение может быть любым, но не больше чем Силы,действующие на тело качения.Уравнение равновесия сил с учетом трения качения. Изучение равновесия тел с учетом трения можно свести к рассмотрению предельного равновесия,которое имеет место,когда сила трения Fтр. = Fпред. При аналитическом решении, реакцию шерховатости изображена двумя состовляющими Если в задача требуется определить условие равновесия при всех значениях, которое может иметь Fтр. То ее можно решить рассмотрев предельное равновесие и уменьшая затем Трение качения. Трение качения называется сопротивление возникающее при качении одного тела по поверхности другого.Это сопративлление обясняет деформацию тел в зоне их контакта. Значение деформации зависит от материала тел и действущих на них сил.ш Центр тяжести твердого тела На каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую Для тел, размеры которых малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполнены эти два условия, называют однородным полем тяжести.
Равнодействующая G сил тяжести, действующих на частицы данного тела, называется весом тела. По модулю вес тела равен произведению его массы m на ускорение свободного падения g Центром тяжести тела называется неизменно связанная с этим телом точка С, через которую проходят линии действия веса тела при любом положении тела в пространстве (см.рис.). Такая точка всегда существует и является примером так называемого центра параллельных сил. Центр тяжести тела является геометрической точкой, которая может распологаться вне пределов данного тела (например, для кольца).
Кинематика.
Пусть точка Р движется в пространстве относительно некоторой системы отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор r, проведенный из начала координат в точку Р. При движении точки Р вектор r будет изменяться с течением времени t, вообще говоря, и по модулю, и по направлению. Следовательно, r является переменным вектором (вектором-функцией), зависящим от аргумента t: r = r (t). Эта векторная функция определяет закон движения точки в векторной форме, так как она позволяет в любой момент времени построить вектор r и найти положение движущейся точки. Геометрическое место концов векторов r (t), называемое также годографом вектора r, определяет траекторию движущейся точки. Как известно, вектор может быть задан аналитически либо его модулем и углами с осями координат, либо его проекциями на эти оси. При прямолинейном движении вектор a направлен вдоль прямой, по которой движется точка. Если траекторией является пространственная кривая, то вектор a направлен в сторону вогнутости траектории и лежит в соприкасающейся плоскости. Так называют плоскость, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении d r = v dt движущейся точки (подробнее это понятие изложено при задании движения точки естественным способом). Для пространственной кривой в каждой ее точке будет, вообще говоря, своя соприкасающаяся плоскость. Для плоской кривой соприкасающаяся плоскость совпадает с плоскостью этой кривой и является общей для всех ее точек.
В качестве единицы измерения ускорения применяется обычно м/с2.
Координатный способ задания движения точки Рассмотрим движение в пространстве точки Р по отношению к декартовой прямоугольной системе координат Oxyz. Проекции rx, ry, rz ее радиуса-вектора r равны декартовым координатам точки: rx= x, ry= y, rz= z (см. рис.). Следовательно, зависимость r (t) будет известна, если будут заданы координаты x, y, z как функции времени. Чтобы знать закон движения точки, то есть ее положение в пространстве в любой момент времени, надо задать зависимость координат точки по времени: x = x(t); y = y(t); z = z(t). Эти зависимости представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения. Движение точки можно задавать с использованием и других систем координат, например, вполярных координатах. Если движение точки происходит все время в одной и той же плоскости, то, приняв эту плоскость за координатную плоскость Oxy, получим в этом случае два уравнения движения: x = x(t); y = y(t). При прямолинейном движении точки, если вдоль ее траектории направить ось Ox, движение будет определяться одним уравнением (законом прямолинейного движения точки): x = x(t).
Естественный способ задания движения точки
Пусть кривая АВ является траекторией точки Р при ее движении относительно системы отсчета Oxyz. Выберем на этой траектории какую-нибудь фиксированную точку O*, которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси). Тогда положение точки Р на траектории будет однозначно определяться криволинейной (дуговой) координатой s, которая равна расстоянию от точки O* до точки Р, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка Р перемещается по траектории и, следовательно, координата s будет с течением времени изменяться. Чтобы знать положение точки Р на траектории в любой момент времени, надо знать зависимость s = s(t). Это уравнение и выражает закон движения точки вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо знать:
Заметим, что координата s определяет положение движущейся точки, а не пройденный ею путь. Например, пусть точка Р начинает движение из начала отсчета O* в положительном направлении, доходит до некоторого положения, останавливается и затем перемещается в обратном направлении. Тогда до остановки точки координата s и пройденный ею путь будут совпадать, а после остановки будут отличаться, так как координата s будет уменьшаться, а пройденный путь по-прежнему будет увеличиваться.
18. Определение скорости и ускорения точки при координатном способе задания движения
Связь векторного способа задания движения и координатного дается соотношением
Из определения скорости
Проекции скорости на оси координат равны производным соответствующих координат по времени:
Модуль и направление скорости определяются выражениями
Из определения ускорения
Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени
Модуль и направление ускорения определяются выражениями
Фывфывфывфвфывфыв Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:
Вектор Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению. Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:
Вектор Из рис. 1.1.5 видно, что модуль полного ускорения равен
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.140.197 (0.01 с.) |



 или
или  (1)
(1) достигает такого значения, что при малейшем её увеличении тело начинает скользить.
достигает такого значения, что при малейшем её увеличении тело начинает скользить. и
и  пр. затем составляем обычное уравнение равновесия и просоединяем к ним равенство
пр. затем составляем обычное уравнение равновесия и просоединяем к ним равенство  до 0.
до 0. называют силой тяжести. Эти силы образуют поле силы тяжести.
называют силой тяжести. Эти силы образуют поле силы тяжести. 9.81 м / c2: G = m · g.
9.81 м / c2: G = m · g.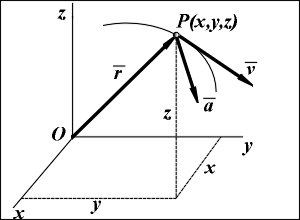 17.Векторный способ задания движения точки
17.Векторный способ задания движения точки Естественным способом задания движения точки удобно пользоваться в тех случаях, когда траектория движущейся точки заранее известна.
Естественным способом задания движения точки удобно пользоваться в тех случаях, когда траектория движущейся точки заранее известна.






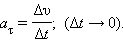
 направлен по касательной к траектории.
направлен по касательной к траектории.

 всегда направлен к центру окружности (см. §1.6).
всегда направлен к центру окружности (см. §1.6).
 , скорость
, скорость  и ускорение
и ускорение 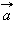 . Путь l является скалярной величиной. Перемещение
. Путь l является скалярной величиной. Перемещение 





