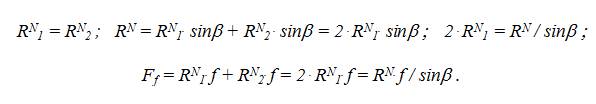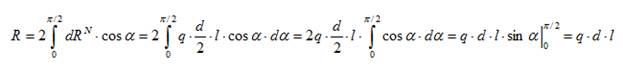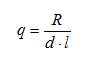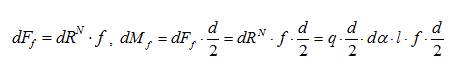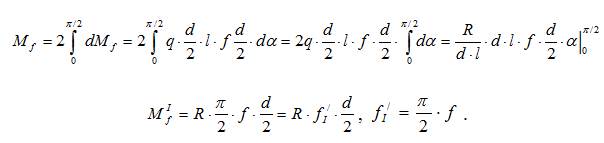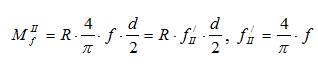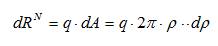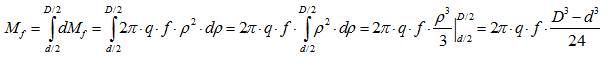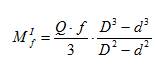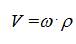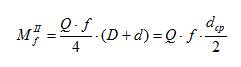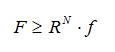Учет формы направляющих, приведенный коэффициент трения

 

На силу трения в поступательной паре влияет также форма направляющих. В технике для обеспечения точности поступательного движения часто используются клинчатые направляющие (они удобны, т.к. автоматически устраняются боковые зазоры в поступательной паре). Рассмотрим ползун, изображенный на рисунке 23, который движется в направляющих, имеющих форму клина.

 

Из баланса сил, действующих на ползун, определяется результирующая нормальная реакция RN. Однако силы трения возникают на боковых поверхностях клина и зависят от нормальных реакций RN1 и RN2, перпендикулярных к этим боковым поверхностям. Результирующая нормальная реакция является геометрической суммой реакций RN1 и RN2:

 

 

Наиболее часто в технике используется симметричное расположение боковых поверхностей клинчатых направляющих. В этом случае:

Как видно, в этом случае в значительной мере можно влиять на величину силы трения изменением угла между плоскостями направляющих (здесь β – половина угла клина). Для дальнейших расчетов вводится понятие приведенного коэффициента трения (обозначается f '):

 

При уменьшении угла β возрастает сила трения на боковых поверхностях клина при одной и той же результирующей нормальной реакции. При применении малых (близких к нулю) углов сила трения увеличивается до очень больших величин (при стремлении угла клина к нулю сила трения стремится к бесконечности). Именно это явление привело к появлению термина «заклинивание».

Этот эффект широко используется в бытовой практике и в технике (например: соединение деревянных строительных конструкций с помощью клиньев; применение для рубки дров специального топора – «колуна» с увеличенным углом заточки для предотвращения застревания при колке дров; применение клиньев для удержания бурильной колонны; применение клиноременных передач для увеличения тяговой способности; в крепежных резьбах для предотвращения самоотвинчивания и др).

 

Трение во вращательных парах

 

В конструкции вращательной пары (шарнира) можно выделить два вида соприкасающихся поверхностей (рисунок 24):

- цилиндрические поверхности вала и отверстия,

- торцовые поверхности соединенных звеньев.

Цилиндрическая опорная поверхность вала (воспринимающая радиальную нагрузку) называется цапфой. (Концевая цапфа называется шипом, цапфа, расположенная в середине вала называется шейкой).

Цилиндрическая часть опоры, работающая с цапфой и воспринимающая радиальные нагрузки, называется подшипником (от слова шип – подшипник).

Торцовая (плоская) часть вала, воспринимающая осевые нагрузки называется пятой. Часть опоры, работающая с пятой и воспринимающая осевые нагрузки, называется упорным подшипником («подпятником»).

 

При решении задачи об определении силы трения во вращательной паре рассматривается две гипотезы:

- по первой гипотезе удельное давление считается распределенным равномерно по опорной поверхности (q=const). Эта гипотеза справедлива для тихоходных валов и плохо прирабатывающихся поверхностей;

- по второй гипотезе расчет ведется с учетом износа поверхностей при работе пары. Она справедлива для быстроходных валов и хорошо прирабатывающихся поверхностей.

 

Трение в цапфах

 

 

Первая гипотеза. Удельное давление по опорной поверхности распределяется равномерно, т.е. q=const (рисунок 25а).

Выделим бесконечно малый элемент поверхности, определяемый центральным углом dα, на расстоянии α от вертикальной оси. На этот элемент действует нормальная реакция dRN, которая определяется через удельное давление и площадь выделенного элемента:

Сумма элементарных нормальных реакций в проекции на вертикальную ось уравновешивает радиальную силу, действующую на цапфу:

 

Получается промежуточный результат, определяющий величину удельного давления:

Однако этот результат имеет большое самостоятельное значение. Он показывает, что удельное давление (а в расчетах на прочность это напряжение смятия на поверхности контактирующих деталей) определяется делением радиальной силы на проекцию площади контакта на диаметральную плоскость вала (а не на полную величину контактной площади). Это положение широко применяется при расчетах деталей машин.

Определим величину элементарной силы трения, действующей на выделенный элемент, и элементарный момент трения от этой силы:

Просуммировав элементарные моменты от силы трения по всей площади контакта, получаем значение момента трения на поверхности цапфы по этой гипотезе:

 

Здесь fI' – приведенный коэффициент трения, вычисляемый по первой гипотезе.

Вторая гипотеза. Расчет ведется с учетом износа поверхности контакта. При этом принимается следующее допущение – изнашивается подшипник, а вал остается неизменным. Это допущение вполне отвечает реальной ситуации, т.к. вал воспринимает все нагрузки от передач, работает в тяжелом режиме, обычно выполняется из качественных сталей, опорные поверхности часто подвергаются термическому упрочнению.

С целью уменьшения потерь на трение (для формирования антифрикционной пары) подшипники скольжения выполняются из более мягких материалов, имеющих в паре со стальным валом пониженные коэффициенты трения (бронзы, баббиты и др.). Понятно, что именно более мягкий материал будет изнашиваться в первую очередь.

В результате износа подшипника вал «просядет» на некоторую величину (рисунок 25б). Из теории износа известно, что величина износа пропорциональна удельному давлению и относительной скорости трущихся поверхностей. Но в данном случае относительная скорость – это окружная скорость на поверхности цапфы, которая во всех точках одна и та же. Поэтому величина износа будет больше в тех местах, где больше удельное давление, т.е. величина износа пропорциональна удельному давлению.

На рисунке 25б показаны два положения вала – в начале работы и после того, как произошел износ поверхности. Изношенный слой представляет собой серповидную фигуру. Но так как износ пропорционален удельному давлению, то эту серповидную фигуру можно принять за эпюру удельного давления, выполненную в некотором масштабе.

Как видно, в результате износа происходит перераспределение удельного давления на поверхности трения. Максимальное давление qmax располагается на линии действия радиальной нагрузки, действующей на вал.

Так как вал в результате износа подшипника опустился на некоторую величину, то расстояние по вертикали для любой точки вала между ее первоначальным и новым положениями одно и то же (и равно qmax). Поэтому текущее значение удельного давления на выделенном элементе, можно выразить приближенно из криволинейного прямоугольного треугольника (рисунок 25 б):

Дальнейший ход решения задачи ничем не отличается от решения по первой гипотезе. В результате получают следующие зависимости для определения момента сил трения по второй гипотезе:

Таким образом, происходит уменьшение приведенного коэффициента трения (примерно на 20%) и, соответственно, снижение потерь на трение и увеличение коэффициента полезного действия. Вот почему все новые машины обязательно проходят обкатку при неполной мощности.

В результате обкатки происходит первичный износ поверхности (сглаживание микронеровностей), происходит приработка поверхностей («притирка» поверхностей одна к другой). Только после этого машина может использоваться на полную мощность.

 

Трение в пятах

 

 

Первая гипотеза. Так как в данном случае опорная поверхность является плоскостью, то постоянное удельное давление (рисунок 26а) определяется простым делением осевого усилия на площадь опорного кольца:

Выделим кольцевой элемент поверхности толщиной dρ на расстоянии ρ от центра пяты (рисунок 26в). Элементарная нормальная реакция, действующая на этот элемент, определяется умножением удельного давления на его площадь:

Определим элементарную силу трения и момент от этой силы трения:

 

Проинтегрировав по всей опорной поверхности, получим общий момент трения:

 

Подставив значение q, окончательно получаем:

Вторая гипотеза. Как показывает практика, по истечении времени происходит равномерный износ опорной поверхности пяты, т.е. произведение удельного давления на относительную скорость величина постоянная:

В данном случае скорость в разных точках контактной поверхности различна:

Но так как для вала угловая скорость едина, то износ будет пропорционален произведению q⋅ρ другими словами это произведение является некоторой константой k:

Таким образом, эпюра удельного давления представляет собой гиперболическую зависимость (рисунок 26б). В результате износа поверхности удельное давление перераспределяется таким образом, что при приближении к оси вращения вала оно резко увеличивается (теоретически увеличиваясь до бесконечности в центре опорной поверхности). Именно поэтому сплошные пяты в технике практически не применяются.

Дальнейшее решение ведется аналогично решению по первой гипотезе. В результате получается следующая зависимость для определения момента от сил трения на опорной поверхности пяты:

В полученном виде сложно сравнивать гипотезы между собой. Поэтому для оценки результатов рассматривают сплошные пяты (d=0):

Сравнение показывает, что приработкой поверхностей пяты достигается эффект, аналогичный тому, который имеет место в цапфах – величина сил трения уменьшается на 20…25%

 

Трение гибких тел

 

Гибкие ленты, ремни, канаты и другие подобные материалы, оказывающие малое сопротивление при изгибе получили широкое применение в машинах в виде ременных и канатных приводов, а также в механизмах грузоподъемных машин, в ленточных тормозах.

При определении силы трения между барабаном и гибкой нитью (лентой) принимается следующее допущение – нить абсолютно гибкая и нерастяжимая. При таком допущении пренебрегают усилиями, затрачиваемыми на деформацию нити – ее изгиб и растяжение. В этом случае, для того, чтобы нить перемещалась по барабану, к сбегающей ветви надо приложить усилие S2, преодолевающее усилие набегающей ветви S1 и силу трения между нитью и барабаном (рисунок 27):

 

 

Центральный угол α, в пределах которого нить касается барабана, называется углом обхвата. Выделим элемент нити, стягиваемый центральным углом dφ, и рассмотрим его равновесие в проекциях на оси X и Y.

Заменив синус бесконечно малого угла самим углом (dφ/2), косинус бесконечно малого угла приравняв единице и, отбросив член второго порядка малости (произведение двух бесконечно малых величин dS.cos(dφ/2)), после несложных преобразований получаем следующие зависимости:

 

Разделив переменные, проинтегрируем полученное уравнение в пределах угла обхвата:

В результате сила трения между гибкой нитью (лентой) и барабаном определяется следующим образом:

Эта формула получена Л. Эйлером и носит его имя.

В данном случае появляется дополнительный фактор – угол обхвата, с помощью которого можно существенно влиять на величину силы трения, что широко используется в технике.

 

Трение качения

 

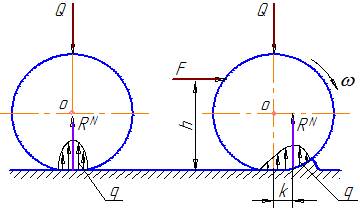
Сопротивление, возникающее при качении одного тела по другому, называется трением качения. Оно обусловлено деформациями этих тел (рисунок 28).

 

 

На рисунке 28 показано два разных состояния одного и того же катка. Слева изображен каток в состоянии покоя. Удельное давление на контактной площадке (которая образуется в результате деформации контактирующих звеньев) распределяется симметрично (по теории Герца – по эллиптическому закону) относительно линии действия приложенной нагрузки. В результате нормальная реакция совпадает с линией действия внешней силы и уравновешивает ее.

Справа каток движется под действием силы F, приложенной к катку на некотором плече h. Происходит перераспределение деформации таким образом, что впереди катка (по ходу движения) образуется волна деформации. Эпюра удельного давления трансформируется и нормальная реакция смещается вперед по ходу движения катка на величину k, создавая момент сопротивления. Этот момент сопротивления называется моментом трения качения, плечо k – коэффициентом трения качения.

Формула для определения момента трения качения аналогична формуле для определения силы трения в поступательной паре (коэффициент трения качения, как и коэффициент трения скольжения, является справочным материалом – определяется экспериментально). Однако надо помнить, что коэффициент трения качения величина размерная – имеет линейную размерность (м, см, мм).

В высшей кинематической паре возможно не только качение одного звена по поверхности другого, но и относительное скольжение соприкасающихся поверхностей. Поэтому представляет интерес условие, при котором будет происходить тот или иной процесс.

Для того чтобы звено катилось, движущий момент должен быть больше момента сопротивления (или равен ему). В данном случае в качестве момента сопротивления выступает момент трения качения:

Для того чтобы звено скользило вдоль поверхности второго, движущая сила должна быть больше силы трения скольжения (или равна ей):

Звено будет двигаться по пути наименьшего сопротивления. Поэтому будет происходить чистое качение, если:

 

 

Соответственно условие чистого скольжения:

При k/h = f происходит неопределенное движение (одновременное качение со скольжением).

Если движущая сила приложена в центре катка, то вместо плеча h надо подставить радиус катка r.

Видно, что с уменьшением радиуса резко возрастает сопротивление качению и, с большей вероятностью, под действием движущей силы каток будет скользить (поэтому колеса транспортных машин, требующих значительной проходимости в любую погоду, – колесные трактора, вездеходы, «внедорожники» – имеют большой диаметр).