Структурная классификация плоских механизмов

 

Среди различных видов классификации механизмов особое место занимает структурная классификация плоских механизмов, основанная на принципе их образования, впервые сформулированном в 1914 году русским ученым Л.В. Ассуром.

В дальнейшем эта теория была развита И.И. Артоболевским и именно в его интерпретации обычно рассматривается данная классификация.

Согласно основному принципу, предложенному Л.В. Ассуром, любой плоский механизм может быть образован путем присоединения к начальному или начальным механизмам так называемых структурных групп (в последствии их стали называть группами Ассура).

Начальный механизм составляют начальное звено со стойкой (начальное звено – это звено, которому приписывается одна или несколько обобщенных координат. Обобщенными координатами механизма называют независимые между собой координаты, определяющие положения всех звеньев механизма относительно стойки.

Чаще всего в качестве начального принимается входное звено механизма, но, в принципе, в качестве начального можно принять любое другое звено, если при этом упрощается анализ механизма). Количество начальных механизмов определяется числом степеней свободы рассматриваемого механизма. По И.И. Артоболевскому начальные механизмы относятся к механизмам I класса.

Структурная группа (группа Ассура) – это такая кинематическая цепь, присоединение которой к любому механизму не изменяет его числа степеней свободы. При этом такая цепь не должна распадаться на более простые цепи с тем же свойством.

Так как группа Ассура не изменяет числа степеней свободы механизма после присоединения к нему или отсоединения от него, то она обладает собственной нулевой степенью свободы. Таким образом:

 

Wгр=3nгр–2p5гр=0,

 

откуда

 

p5гр=3nгр/2

 

или

 

nгр=2p5гр/3,

 

где:

 

nгр – число звеньев в группе Ассура, включая фиктивные звенья, полученные при замене высших пар, p5гр – число кинематических пар пятого класса в группе Ассура, включая пары, полученные при замене высших пар.

Примечание: рассматриваются структурные группы, включающие только низшие пары 5 класса, т.к. при наличии высших кинематических пар в механизме их можно заменить цепями с низшими парами.

Так как количество звеньев и кинематических пар заведомо целые числа, то число звеньев в группе Ассура всегда четное, а число кинематических пар кратно трем. Таким образом группы Ассура имеют следующие сочетания чисел звеньев и кинематических пар (таблица 2.1):

 

Таблица 2.1.

 

nгр
p5гр

 

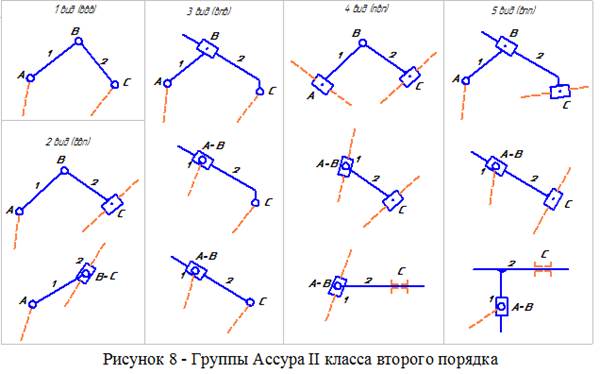
Группы Ассура подразделяются на классы, порядки.

Класс группы Ассура определяется числом сторон замкнутого контура (многоугольника), входящего в состав этой группы. При этом все группы, имеющие два звена, относятся к группам II класса, а контур с числом сторон больше трех должен быть подвижным (т.е. иметь изменяемую форму при работе механизма).

Порядок группы Ассура определяется числом элементов кинематических пар, которыми группа присоединяется к механизму.

Группы Ассура второго класса одновременно являются группами второго порядка (иногда их называют двухповодковыми группами), но они еще подразделяются на виды.

Вид группы Ассура зависит от сочетания вращательных (шарниров) и поступательных (ползунов) кинематических пар в данной группе. Всего существует пять видов групп Ассура второго класса.

Класс механизма определяется наивысшим классом групп Ассура, входящих в его состав.

На рисунках 8…9 приведены примеры схематического изображения групп Ассура различных классов. Пунктирными линиями изображены звенья механизма, к которым присоединяется данная группа (они не входят в состав группы).

Как было отмечено выше, простейшие группы, включающие в свой состав два звена и три кинематические пары пятого класса, относятся к группам Ассура II класса (по И.И. Артоболевскому). Все они имеют два свободных элемента кинематических, которыми присоединяются к другим звеньям механизма (на рисунке 8 – это элементы А и С), поэтому одновременно являются группами второго порядка (в связи с этим обычно о порядке групп Ассура второго класса не говорят).

Группа Ассура второго класса, имеющая в своем составе все три вращательные пары (шарниры), условно отнесена к группе первого вида. Последующие виды образуются последовательным замещением вращательных пар поступательными («ползунами»).

Заменой одной крайней вращательной пары поступательной парой образуется группа второго вида.

Замена среднего шарнира на поступательную пару образует группу третьего вида.

Группа четвертого вида получается при замене двух крайних вращательных пар на поступательные и, наконец, заменой одной крайней вращательной пары и средней пары на поступательные формируется группа пятого вида.

Для лучшего запоминания и определения вида группы при структурном анализе механизмов можно воспользоваться аббревиатурой пар, входящих в ее состав: ВВВ (вращательная-вращательная-вращательная) – группа 1 вида; ВВП (вращательная-вращательная-поступательная) – группа 2 вида; ВПВ – группа 3 вида; ПВП – группа 4 вида; ВПП – группа 5 вида.

 

 

На рисунке 8 представлены группы второго класса всех пяти видов. В верхнем ряду группы изображены в самом общем случае. Однако на практике многие размеры задаются таким образом, что конфигурация групп значительно трансформируется. Поэтому для лучшей ориентации в таблице приведены некоторые частные случаи, которые могут встретиться при анализе механизмов.

На рисунке 9 представлены примеры структурных групп более высоких классов. На рисунке представлены группы только с вращательными парами, что облегчает понимание класса и порядка групп Ассура. На самом деле в любом месте группы вместо вращательной пары может быть поставлена поступательная, что принципиально не меняет сути классификации.

 

 

Ценность структурной классификации механизмов заключается в том, что группы Ассура обладают постоянными свойствами, независимо от того в каком механизме они находятся, в какой сфере жизнедеятельности применяется данный механизм.

Это дает возможность иметь универсальные методы исследования любых механизмов через разработку методов исследования отдельных групп Ассура. Таким образом, установив класс механизма, фактически определяют порядок анализа и методы решения задач, связанных с его работой.