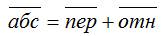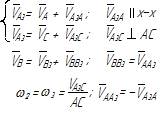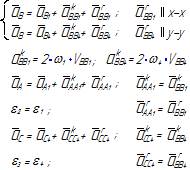Графический Метод как алгоритм решения задачи с помощью эвм

Графический метод кинематического исследования механизмов дает наглядное представление о движении исследуемого звена в пределах всего цикла работы механизма. Вместе с тем, при необходимости исследования характера движения нескольких звеньев, а также многих характерных точек механизма, метод становится весьма трудоемким (громоздким). Кроме того значительным недостатком метода является его сравнительно низкая точность.

С развитием электронно-вычислительной техники сложилось впечатление, что методы графического исследования «ушли в прошлое» и на первый план должны выйти чисто аналитические (принципиально точные) методы.

Однако на самом деле графические методы решения задач приобретают новое значение, если их использовать в качестве алгоритмов машинного решения задач.

Такое применение графических методов кинематического исследования механизмов позволяет значительно упростить решение, упростить программы машинного счета и, что самое ценное, сделать эти программы универсальными (т.е. решение ведется по единой программе для любого механизма, для любого звена или точки, для чего достаточно ввести в данную программу только уравнение перемещений исследуемого звена или точки, полученное аналитически для исследуемого механизма).

При этом устраняется и основной недостаток метода – низкая точность, т.к. с помощью ЭВМ можно добиться практически любой разумной наперед заданной степени точности. Кроме того при машинном решении задачи можно обеспечить вывод информации для любого числа положений механизма и в любой форме (в численной форме в виде таблиц, в графическом представлении на дисплее, в виде распечатки диаграмм на принтере или их изображении, полученном с помощью плоттера).

 

3.5 Метод планов скоростей и ускорений

 

Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов.

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное - движение данной точки относительно той, движение которой принято за переносное:

 

 

Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:

 

 

Планы скоростей и ускорений обладают следующими свойствами:

- на плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана. На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает;

- отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек. Вектор относительной скорости направлен на плане к той точке, которая в индексе скорости стоит на первом месте;

- фигуры, образованные точками одного и того же жесткого звена на плане и на механизме, подобны. Поэтому, если на звене известны скорости и ускорения двух точек, то скорость и ускорение любой третьей точки этого же звена можно найти по подобию;

- имея план скоростей, можно найти угловую скорость любого звена механизма. Для определения угловой скорости исследуемого звена надо взять относительную скорость двух любых точек данного звена и разделить на расстояние между этими точками на механизме;

- имея план ускорений, можно найти угловое ускорение любого звена механизма. Для определения углового ускорения исследуемого звена надо взять тангенциальную составляющую относительного ускорения двух любых точек данного звена и разделить на расстояние между этими точками на механизме;

- звенья, соединенные в поступательную кинематическую пару, имеют одинаковые угловые скорости и одинаковые угловые ускорения.

При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:

1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).

В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.

 

 

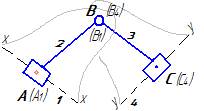
Для примера, приведенного на рисунке 13, нормальное ускорение точки В относительно точки А будет направлено вдоль радиуса ВА к точке А. Тангенциальное – перпендикулярно этому радиусу;

2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей (рисунок 14).

 

 

Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С1, принадлежащей этой направляющей.

Движение точки С1 принимается в качестве переносного. Движение точки С2, принадлежащей ползуну, относительно точки С1 получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С1 и С2 совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).

Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится. Уравнения планов для групп Ассура второго класса приведены в таблице 3.1.

 

Таблица 3.1 – Кинематический анализ групп Ассура II класса методом планов

 

вид группы	конфигурация группы	Уравнения для построения планов скоростей и для определения угловых скоростей	уравнения для построения планов ускорений и для определения угловых ускорений