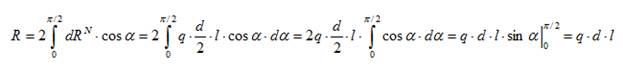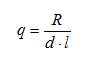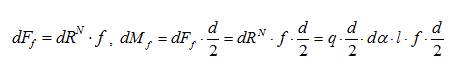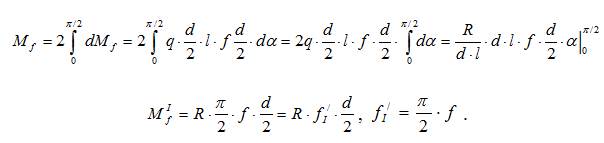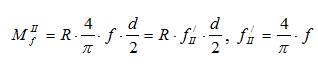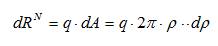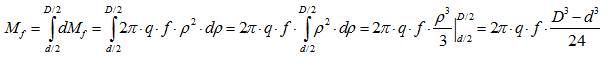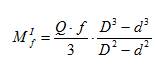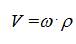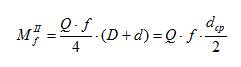Курс теории механизмов и машин

Курс теории механизмов и машин

Основные понятия теории механизмов и машин

 

Введение

 

Курс теории механизмов и машин является переходной ступенью в цепи механической подготовки инженера – он опирается на фундаментальные знания, полученные студентом при изучении математики, физики, теоретической механики и является базой для изучения последующих практических (специальных) дисциплин механического цикла (прежде всего для курса «Детали машин и основы конструирования»).

Целью изучения дисциплины "теория механизмов и машин" является формирование необходимой начальной базы знаний по общим методам анализа и синтеза механических систем, положенных в основу технологического оборудования, применяемого в сфере будущей профессиональной деятельности выпускников высших технических учебных заведений.

 

Машина

 

Машина – есть устройство, выполняющее механические движения для преобразования энергии, материалов и информации в целях замены или облегчения физического и умственного труда человека.

С точки зрения выполняемых функций машины можно разделить на следующие классы:

- энергетические машины (машины-двигатели, машины-генератора).

- рабочие машины (транспортные и технологические).

- информационные машины (для получения и преобразования информации).

- кибернетические машины (заменяющая или имитирующая различные механические, физиологические или биологические процессы, присущие человеку и живой природе, и обладающая элементами искусственного интеллекта – роботы, автоматы).

Развитое машинное устройство, состоящее из двигателя, передаточных механизмов и рабочей машины (а в некоторых случаях контрольно-управляющих и счетно-решающих устройств) называется машинным агрегатом.

 

Основные понятия элементов машин

Деталь – составная часть механического устройства, выполненная без применения сборочных операций (например: болт, гайка, вал, станина станка, полученная литьем и т.д.).

Звено – это деталь или группа деталей, представляющих с кинематической точки зрения единое целое (т.е. группа деталей, жестко соединенных между собой и движущихся как единое твердое тело).

Кинематическая схема – это условное изображение звеньев и всего механизма, выполненное строго в масштабе.

При составлении кинематической схемы выделяются основные элементы звена, которыми оно присоединяется к другим звеньям механизма (отверстия, направляющие и т.д.). Эти элементы изображаются условно (например, отверстии – в виде окружностей произвольного радиуса) и соединяются жесткими стержнями.

Под масштабом в теории механизмов и машин понимают «цену» одного миллиметра. Такое понимание масштаба (иногда его называют масштабным коэффициентом) очень удобно при анализе работы механизма, т.к. является универсальным и позволяет представлять в виде отрезка любую физическую величину, что очень важно при использовании графических и графоаналитических методов исследования.

Аналогично можно представлять в виде отрезков любые величины (перемещения звеньев, скорости, ускорения, время, силы и т.д.) на планах, диаграммах, различных графиках и др.

В зависимости от характера движения звенья могут иметь собственные названия, например:

-кривошип – звено, совершающее вращательное движение вокруг неподвижной оси и делающее при этом полный оборот;

-коромысло – звено, совершающее возвратно-вращательное движение;

-ползун – звено, движущееся поступательно;

-шатун – звено, совершающее сложное плоско-параллельное движение;

-кулиса – коромысло (или, иногда, кривошип), по которому движется ползун;

-стойка – звено, принятое за неподвижное (по определению звена стойка в механизме может быть только одна – все неподвижные детали обязательно крепятся на некоторой станине, корпусе, картере, основании и представляют одну жесткую конструкцию, т.е. одно звено).

На кинематической схеме стойка обычно изображается в виде отдельных фрагментов в тех местах, где к ней присоединяются другие звенья механизма, что резко упрощает эту схему.

Кинематическая пара - подвижное соединение двух звеньев.

Кинематические пары классифицируются по различным признакам:

1) по числу связей, накладываемых на относительное движение звеньев, соединенных в кинематическую пару. По этому признаку кинематические пары подразделяются на классы. Приняты следующие обозначения:

W – число степеней свободы

S – число связей, накладываемых на относительное движение звеньев.

Свободное звено в пространстве имеет шесть степеней свободы. При соединении звеньев некоторые из этих степеней свободы отнимаются ("накладываются связи"). Зависимость между числом накладываемых связей и оставшимся числом степеней свободы в относительном движении звеньев очевидна:

W=6–S или S=6–W,

таким образом, существует пять классов кинематических пар (если отнять все шесть степеней свободы, то получится неподвижное соединение).

Примеры кинематических пар:

Шар относительно плоскости, не отрываясь от нее, может совершать вращательные движения вокруг всех трех осей координат, а также двигаться вдоль осей "X" и "Y". При движении вдоль оси "Z" шар оторвется от плоскости, т.е. будет два свободных звена – кинематическая пара перестанет существовать. Таким образом, на относительное движение звеньев накладывается одна связь – это кинематическая пара I класса.

Цилиндр относительно плоскости, без нарушения характера контакта нельзя цилиндр переместить вдоль оси "Z" и повернуть вокруг оси "Y", т.е. число связей равно двум – пара II класса.

Плоскость относительно другой плоскости без нарушения характера контакта может двигаться поступательно вдоль осей "X" и "Y", а также вращаться вокруг оси "Z". Невозможно поступательное движение вдоль оси "Z" и вращательные движения вокруг осей "X" и "Y". Таким образом, число связей равно трем – кинематическая пара III класса.

 

W = 5 W = 4 W = 3

S = 1 => I кл. S = 2 => II кл. S = 3 => III кл.

 

 

 

Примеры кинематических пар

 

Например, болт с гайкой составляют кинематическую пару пятого класса. В данном случае имеется два движения гайки при неподвижном болте – вращательное движение вокруг оси болта и поступательное движение вдоль этой оси, но нельзя переместить гайку вдоль оси, не повернув ее, или повернуть гайку так, чтобы она не переместилась вдоль оси. Эти два движения образуют одно сложное (в данном случае – винтовое) движение. Оно определяет одну степень свободы в относительном движении этих звеньев, т.е. число связей равно пяти;

2) по характеру контакта звеньев, соединенных в кинематическую пару. По этому признаку кинематические пары подразделяются на высшие и низшие. Высшие пары имеют точечный или линейный контакт звеньев, составляющих данную кинематическую пару. В низшей паре звенья контактируют друг с другом по какой-либо поверхности (в частном случае по плоскости).

Низшие кинематические пары обладают большей несущей способностью, т.к. имеют большую площадь контакта (в высшей паре площадь контакта теоретически равна нулю, а реально получается за счет деформации элементов кинематической пары – «пятно контакта"). Но в низших парах при работе происходит скольжение одной поверхности относительно другой, в то время как в высших парах может происходить и скольжение и качение.

Как правило, сопротивление скольжению больше, чем сопротивление перекатыванию одной поверхности относительно другой, т.е. потери на трение в высшей паре (если использовать только качение) меньше по сравнению с низшей парой (поэтому для увеличения коэффициента полезного действия вместо подшипников скольжения обычно ставят подшипники качения).

Кинематические пары: шар и плоскость, цилиндр и плоскость - являются высшими, а пара плоскость и плоскость – низшая.

3) по траектории движения точек, принадлежащих звеньям, составляющим кинематическую пару. По этому признаку выделяют пространственные и плоские кинематические пары.

В плоской кинематической паре все точки движутся в одной или в параллельных плоскостях, а траектории их движения представляют собой плоские кривые. В пространственных парах точки движутся в различных плоскостях и имеют траектории в виде пространственных кривых.

Значительное число механизмов, применяемых на практике, являются плоскими механизмами, поэтому необходимо более подробно рассмотреть плоские кинематические пары.

Свободное звено, помещенное в плоскость, имеет три степени свободы (поступательные движения вдоль осей координат и вращательное вокруг оси, перпендикулярной данной плоскости). Таким образом, размещение звена в плоскости отнимает у него три степени свободы (накладывает три связи). Но соединение данного звена с другим в кинематическую пару накладывает на относительное движение еще связи (минимальное число – 1). В результате на плоскости могут существовать только кинематические пары, имеющие две или одну степень свободы в относительном движении.

По общей классификации это пары четвертого и пятого классов. Простейшие пары пятого класса обеспечивают только одно движение – вращательное или поступательное (вращательная кинематическая пара в технике называется шарниром, поступательную пару по аналогии с поступательно движущимся звеном иногда также называют ползуном).

Две степени свободы в относительном движении на плоскости обычно обеспечивают два соприкасающихся профиля (на кинематической схеме контакт в точке, в реальном механизме это возможно линия, которая проецируется в точку). Таким образом, плоские кинематические пары пятого класса (шарниры и ползуны) одновременно являются низшими парами, а кинематические пары четвертого класса – высшими парами.

 

Примеры кинематических пар:

 

 

 

4) по характеру замыкания звеньев, соединенных в кинематическую пару. Существует два вида кинематических пар, отличающихся друг от друга по этому признаку. Кинематические пары с геометрическим замыканием и кинематические пары с силовым замыканием.

В парах с геометрическим замыканием конфигурация звеньев препятствует их разъединению в процессе работы. Например, присоединение шатуна к коленчатому валу при помощи шатунной крышки, или любые другие шарниры (дверь с косяком, окно с оконной рамой и т.д.).

В парах с силовым замыканием контакт звеньев в процессе работы обеспечивается постоянно действующей силой. В качестве замыкающей силы выступает вес. Если веса недостаточно, то обычно для создания прижимающего усилия применяют различные упругие элементы (чаще всего пружины).

Кинематическая цепь – это сочетание звеньев, соединенных в кинематические пары.

Имеется определенная классификация кинематических цепей – цепи могут быть простыми и сложными, замкнутыми (закрытыми) и разомкнутыми (открытыми), пространственными и плоскими.

Механизм - кинематическая цепь, имеющая стойку (т.е. звено, принятое за неподвижное), в которой движение одного или нескольких звеньев полностью определяет характер движения остальных звеньев этой цепи.

Звенья, законы движения которых заданы, называются входными.

Звенья, законы которых надо определить, называются выходными. Количество входных звеньев определяется числом степеней свободы кинематической цепи, положенной в основу данного механизма.

Понятия входное и выходное (вход и выход) – это кинематическая характеристика. Не надо путать с понятиями – ведущее звено и ведомое звено. Ведущим звеном называется звено, к которому подводится мощность; ведомое звено – звено, с которого снимается мощность (для выполнения полезной работы).

Таким образом, понятия ведущее и ведомое звено – это силовая (энергетическая) характеристика. Однако в подавляющем большинстве случаев входное звено одновременно является и ведущим, выходное звено – ведомым.

 

Основные виды механизмов

 

По функциональному назначению механизмы обычно делятся на следующие виды:

- механизмы двигателей и преобразователей (осуществляют преобразование различных видов энергии в механическую работу или наоборот);

- передаточные механизмы (осуществляет передачу движения от двигателя к технологической машине или исполнительному механизму, преобразуя это движение в необходимое для работы данной технологической машины или исполнительного механизма);

- исполнительные механизмы (изменение формы, состояния, положения и свойств обрабатываемой среды или объекта);

- механизмы управления, контроля и регулирования (для обеспечения и контроля размеров обрабатываемых объектов);

- механизмы подачи, транспортировки, питания и сортировки обрабатываемых сред и объектов (механизмы винтовых шнеков, скребковых и ковшевых элеваторов для транспортировки и подачи сыпучих материалов, механизмы загрузочных бункеров для штучных заготовок, механизмы сортировки готовой продукции по размерам, весу, конфигурации и т.д.);

- механизмы автоматического счета, взвешивания и упаковки готовой продукции (применяются во многих машинах, в основном выпускающих массовую штучную продукцию).

По общим методам синтеза и анализа работы выделяются следующие виды механизмов:

- механизмы с низшими парами (рычажные механизмы)

- кулачковые механизмы

- зубчатые механизмы

- фрикционные механизмы

- механизмы с гибкими связями

- механизмы с деформируемыми звеньями (волновые передачи)

- гидравлические и пневматические механизмы.

 

 

Задачи кинематики

Кинематический анализ – это исследование движения звеньев механизма без учета сил, вызывающих данное движение. При кинематическом анализе решаются следующие задачи:

- определение положений звеньев, которые они занимают при работе механизма, а также построение траекторий движения отдельных точек механизма;

- определение скоростей характерных точек механизма и определение угловых скоростей его звеньев;

- определение ускорений отдельных точек механизма и угловых ускорений его звеньев.

При решении задач кинематического анализа используются все существующие методы – графический, графоаналитический (метод планов скоростей и ускорений) и аналитический. При кинематическом анализе в качестве начального звена принимается входное звено (звено, закон движения которого задан), т.е. входное звено со стойкой составляют начальный механизм – с него начинается решение задачи.

Далее решение ведется по группам Ассура в порядке их присоединения к механизму.

 

Динамика механизмов и машин

Задачи динамики

 

В данном разделе изучается движение звеньев механизма с учетом действующих на них сил. При этом рассматриваются следующие основные задачи динамики:

1) изучение сил, действующих на звенья механизма, и определение неизвестных сил при заданном законе движения на входе;

2) задача об энергетическом балансе машины;

3) установление истинного закона движения под действием заданных сил;

4) регулирование хода машины;

5) уравновешивание сил инерции;

6) динамика приводов.

 

Силовой расчет механизмов

 

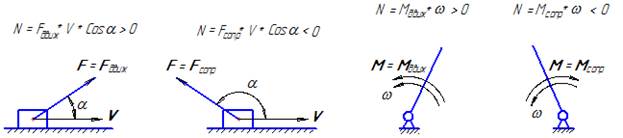
Силовой расчет механизмов относится к решению первой задачи динамики. Как видно из содержания задач динамики, приведенного выше, первая задача включает в себя две части: изучение сил, действующих на звенья механизма; определение неизвестных сил при заданном законе движения на входе (эта вторая часть и есть задача силового расчета).

В целях дальнейшего понимания терминологии и систематизации материала целесообразно повторить известные из физики и теоретической механики сведения о силах, а также ввести некоторые новые (применяемые в теории механизмов и машин) понятия. С точки зрения решения задач динамики силы (в данном случае под силой понимается обобщенное понятие силового фактора – собственно сила или момент) можно классифицировать следующим образом:

а) по взаимодействию звена механизма с другими объектами. По этому признаку силы подразделяются на внешние и внутренние:

- внешние силы – это силы взаимодействия звена механизма с какими-то телами или полями, не входящими в состав механизма;

- внутренние силы – это силы взаимодействия между звеньями механизма (реакции в кинематических парах);

- движущая сила – это сила, которая помогает движению звена и развивает положительную мощность;

б) по мощности, развиваемой силой. По этому признаку силы делятся на силы движущие и силы сопротивления (рисунок 16):

- сила сопротивления препятствует движению звена и развивает отрицательную мощность.

 

 

В свою очередь силы сопротивления можно разделить на силы полезного сопротивления и силы вредного сопротивления:

- силы полезного сопротивления – это силы, для преодоления которых и создан механизм. Преодолевая силы полезного сопротивления, механизм создает полезную работу (например, преодолевая сопротивления резанию на станке, добиваются необходимого изменения формы детали; или, преодолевая сопротивление воздуха в компрессоре, сжимают его до требуемого давления и т.д.);

- силы вредного сопротивления – это силы, на преодоление которых затрачивается мощность и эта мощность теряется безвозвратно. Обычно в качестве вредных сил сопротивления выступают силы трения, гидравлического и аэродинамического сопротивлений. Работа по преодолению этих сил переводится в тепло и рассеивается в пространство, поэтому коэффициент полезного действия любого механизма всегда меньше единицы;

в) силы веса – это силы взаимодействия звеньев механизма с гравитационным полем земли;

г) силы трения – силы, сопротивляющиеся относительному перемещению соприкасающихся поверхностей;

д) силы инерции – силы, возникающие при неравномерном движении звена и сопротивляющиеся его ускорению (замедлению). Сила инерции действует на то тело, которое заставляет ускоряться (замедляться) данное звено. В общем случае при неравномерном движении возникает сила инерции и момент сил инерции:

Fин=-m. as, Mин=-Is. e,

где

Fин – главный вектор сил инерции, приложенный в центре масс звена;

Mин – главный момент сил инерции;

m – масса звена;

Is – момент инерции звена относительно центра масс;

as – ускорение центра масс звена;

e – угловое ускорение звена.

Знак минус в формулах показывает, что сила инерции направлена противоположно ускорению центра масс звена, а момент сил инерции направлен противоположно угловому ускорению звена. Знак силы или момента учитывается только при установлении истинного направления силы или момента на расчетной схеме, а в аналитических вычислениях используется абсолютные их значения.

 

 

При силовом анализе механизмов могут встретиться различные случаи, когда один или оба силовых инерционных фактора могут иметь нулевое значение. На рисунке 17, приведенном выше, показаны некоторые случаи возникновения сил и моментов сил инерции при движении звеньев механизма.

Непосредственно силовой расчет сводится к определению неизвестных сил, действующих на звенья механизма. Как известно из теоретической механики для определения неизвестных сил используются уравнения статики.

Механизм же является неравновесной системой, т.к. большинство его звеньев имеет неравномерное движение, а точки, принадлежащие этим звеньям, движутся по сложным криволинейным траекториям (напомним: состояние равновесия – это состояние покоя или прямолинейного равномерного движения).

 

Поэтому для решения поставленной задачи применяется метод кинетостатики. Метод кинетостатики основан на принципе Даламбера: если ко всем внешним силам, действующим на звенья механизма, добавить силы инерции и моменты сил инерции, то данный механизм будет находиться в состоянии статического равновесия. То есть это искусственный прием, приводящий неравновесную систему в состояние равновесия.

Искусственность приема заключается в том, что силы инерции прикладываются не к тем телам, которые заставляют двигаться звенья ускоренно (замедленно), а к самим звеньям.

Применив этот прием, в дальнейшем можно производить силовой расчет с использованием уравнений статики. Однако, чтобы решить задачу с помощью только уравнений равновесия, система должна быть статически определимой.

Условие статической определимости плоской кинематической цепи:

Для каждого звена, расположенного в плоскости, можно составить три независимых уравнения статики. Если в кинематической цепи имеется "n" подвижных звеньев, то в совокупности для этой цепи можно записать 3n независимых уравнений статики (равновесия). Эти уравнения используются для определения реакций в кинематических парах и неизвестных внешних сил.

На плоскости существуют кинематические пары только пятого и четвертого классов. Пары пятого класса представлены вращательной кинематической парой (шарниром) и поступательной парой (соединение ползуна с направляющей). В шарнире усилие между звеньями может передаваться в любом направлении, поэтому у реакции в шарнире неизвестными являются величина и направление (два компонента), т.е. для определения полной реакции во вращательной паре надо затратить два уравнения статики.

В первом приближении расчет ведется без учета сил трения. В этом случае перемещению ползуна вдоль направляющей ничто не препятствует. Перемещаться же поперек направляющей и поворачиваться ползун не может, поэтому в поступательной паре реакция направлена перпендикулярно направляющей и возникает реактивный момент, препятствующий повороту ползуна.

При силовом расчете обычно реактивный момент не определяют, а находят условную точку приложения реакции (произведение реакции на расстояние до ее условной точки приложения и есть реактивный момент). На определение реакции в поступательной паре также надо затратить два уравнения статики (определить два компонента – величину и точку приложения). Таким образом, на определение полной реакции в кинематической паре пятого класса необходимо затратить два уравнения статики.

Пары четвертого класса (высшие пары) на плоскости представляют соприкасающиеся между собой профили. В высшей паре усилие между звеньями передается по общей нормали к касающимся профилям (без учета сил трения). Поэтому в высшей паре четвертого класса реакция неизвестна только по величине (точка приложения реакции в точке контакта профилей, направление вдоль общей нормали к этим профилям).

Таким образом, для определения реакции в паре четвертого класса надо затратить одно уравнение статики (определить один компонент – величину реакции).

Если в кинематической цепи количество пар пятого класса равно Р5, то на определение реакций во всех этих парах надо затратить 2Р5 уравнений статики. На определение реакций во всех парах четвертого класса используется число уравнений, равное количеству этих пар Р4.

Таким образом, из 3n независимых уравнений статики 2Р5 уравнений используются для определения реакций в парах пятого класса и Р4 – для определения реакций в парах четвертого класса. Оставшиеся уравнения используются для определения неизвестных внешних сил, действующих на звенья механизма.

Пусть X – число уравнений, оставшихся для определения неизвестных внешних сил, тогда

X=3n–2Р5–Р4,

но эта формула совпадает с формулой Чебышева для определения числа степеней свободы плоской кинематической цепи. В результате можно сформулировать условие статической определимости кинематической цепи следующим образом: кинематическая цепь статически определима в том случае, когда число неизвестных внешних сил, действующих на ее звенья, не превышает числа степеней свободы этой цепи.

Так как методы решения разработаны для групп Ассура, то необходимо сформулировать условие статической определимости группы Ассура. Группа Ассура – это кинематическая цепь, имеющая собственную степень свободы, равную нулю. Поэтому группа Ассура статически определима, если на ее звенья не действуют неизвестные внешние силы. Уравнений в группе Ассура достаточно лишь для определения реакций в кинематических парах. Это обстоятельство предопределяет порядок силового расчета механизма:

- разбивают механизм на группы Ассура, взяв в качестве начального то звено, на которое действует неизвестная внешняя сила;

- решение начинают с последней присоединенной группы и заканчивают начальным звеном.

При таком подходе на группы Ассура всегда будут действовать только известные внешние силы и из рассмотрения их равновесия будут определены реакции в кинематических парах, а из рассмотрения условий равновесия начальных звеньев будут определены оставшиеся реакции и неизвестные внешние силы.

Поскольку решение ведется по группам Ассура, то ниже рассматривается принцип силового расчета групп на примере групп второго класса.

 

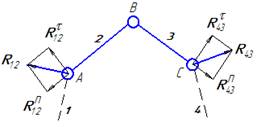
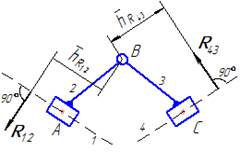
Группа 1 вида

 

Составить: ∑ mB(2)=0; ∑ mB(3)=0; ∑ F(2,3)=0; ∑ F(2)=0

 

Определить: R12t; R43t; R12n; R43n; R32

 

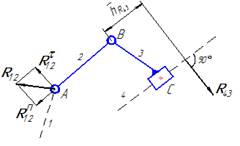
Заменить реакцию R12 составляющими R12n II AB и R12t⊥ AB

Группа 2 вида

 

 

Составить: ∑ mB(2)=0; ∑ F(2,3)=0; ∑ mB(3)=0; ∑ F(2)=0

 

Определить: R12t; R12n; R43; R43; R32

 

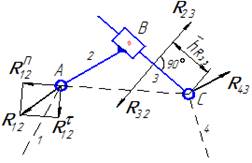
Заменить реакцию R12 составляющими R12n II AC и R12t⊥ AC

Группа 3 вида

 

 

Составить: ∑ mC(2,3)=0; ∑ F(2)=0; ∑ mC(3)=0; ∑ F(3)=0

 

Определить: R12t; R12n; R32n; h23; R43

 

Группа 4 вида

 

 

Составить: ∑ F(2,3)=0; ∑ mB(2)=0; ∑ mB(3)=0; ∑ F(2)=0

 

Определить: R12; R43; h12; h43; R32

 

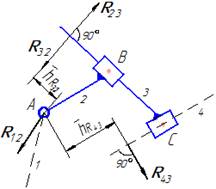
Группа 5 вида

 

 

 

Составить: ∑ F(3)=0; ∑ mA(2)=0; ∑ mA(2,3)=0; ∑ F(2)=0

 

Определить: R23; R43; h32; h43; R12

 

В таблице приняты следующие обозначения и упрощения:

- звенья исследуемой группы обозначены номерами 2 и 3;

- от звена 2 отсоединено звено 1, поэтому приложена реакция R12 (действие отсоединенного звена 1 на рассматриваемое звено 2);

- от звена 3 отсоединено звено 4, поэтому к звену 3 приложена реакция R43;

- черта над обозначением реакции означает, что в данном пункте реакция определена как по величине, так и по направлению (т.е. имеется изображение этого вектора на плане сил);

- с целью уменьшения загромождения чертежа и улучшения наглядности внешние силы, приложенные к звеньям рассматриваемой группы, на рисунке не приведены (надо только иметь ввиду, что все внешние силы, действующие на звенья группы Ассура, известны – это определяется порядком силового расчета механизма).

 

Учет трения в механизмах

 

По физическим особенностям различают трение внутреннее и внешнее.

Внутреннее трение – это процессы, происходящие в твердых, жидких и газообразных телах при их деформации и приводящие к необратимому рассеянию механической энергии. Внутренне трение проявляется в затухании свободных колебаний.

Внешнее трение – это сопротивление относительному перемещению, возникающему между двумя телами в зонах соприкосновения поверхностей, то есть в кинематических парах. По кинематическому признаку различают: трение скольжения, возникающее при скольжении одного тела по поверхности другого, и трение качения, возникающее при качении одного тела по поверхности другого.

Трение в цапфах

 

 

Первая гипотеза. Удельное давление по опорной поверхности распределяется равномерно, т.е. q=const (рисунок 25а).

Выделим бесконечно малый элемент поверхности, определяемый центральным углом dα, на расстоянии α от вертикальной оси. На этот элемент действует нормальная реакция dRN, которая определяется через удельное давление и площадь выделенного элемента:

Сумма элементарных нормальных реакций в проекции на вертикальную ось уравновешивает радиальную силу, действующую на цапфу:

 

Получается промежуточный результат, определяющий величину удельного давления:

Однако этот результат имеет большое самостоятельное значение. Он показывает, что удельное давление (а в расчетах на прочность это напряжение смятия на поверхности контактирующих деталей) определяется делением радиальной силы на проекцию площади контакта на диаметральную плоскость вала (а не на полную величину контактной площади). Это положение широко применяется при расчетах деталей машин.

Определим величину элементарной силы трения, действующей на выделенный элемент, и элементарный момент трения от этой силы:

Просуммировав элементарные моменты от силы трения по всей площади контакта, получаем значение момента трения на поверхности цапфы по этой гипотезе:

 

Здесь fI' – приведенный коэффициент трения, вычисляемый по первой гипотезе.

Вторая гипотеза. Расчет ведется с учетом износа поверхности контакта. При этом принимается следующее допущение – изнашивается подшипник, а вал остается неизменным. Это допущение вполне отвечает реальной ситуации, т.к. вал воспринимает все нагрузки от передач, работает в тяжелом режиме, обычно выполняется из качественных сталей, опорные поверхности часто подвергаются термическому упрочнению.

С целью уменьшения потерь на трение (для формирования антифрикционной пары) подшипники скольжения выполняются из более мягких материалов, имеющих в паре со стальным валом пониженные коэффициенты трения (бронзы, баббиты и др.). Понятно, что именно более мягкий материал будет изнашиваться в первую очередь.

В результате износа подшипника вал «просядет» на некоторую величину (рисунок 25б). Из теории износа известно, что величина износа пропорциональна удельному давлению и относительной скорости трущихся поверхностей. Но в данном случае относительная скорость – это окружная скорость на поверхности цапфы, которая во всех точках одна и та же. Поэтому величина износа будет больше в тех местах, где больше удельное давление, т.е. величина износа пропорциональна удельному давлению.

На рисунке 25б показаны два положения вала – в начале работы и после того, как произошел износ поверхности. Изношенный слой представляет собой серповидную фигуру. Но так как износ пропорционален удельному давлению, то эту серповидную фигуру можно принять за эпюру удельного давления, выполненную в некотором масштабе.

Как видно, в результате износа происходит перераспределение удельного давления на поверхности трения. Максимальное давление qmax располагается на линии действия радиальной нагрузки, действующей на вал.

Так как вал в результате износа подшипника опустился на некоторую величину, то расстояние по вертикали для любой точки вала между ее первоначальным и новым положениями одно и то же (и равно qmax). Поэтому текущее значение удельного давления на выделенном элементе, можно выразить приближенно из криволинейного прямоугольного треугольника (рисунок 25 б):

Дальнейший ход решения задачи ничем не отличается от решения по первой гипотезе. В результате получают следующие зависимости для определения момента сил трения по второй гипотезе:

Таким образом, происходит уменьшение приведенного коэффициента трения (примерно на 20%) и, соответственно, снижение потерь на трение и увеличение коэффициента полезного действия. Вот почему все новые машины обязательно проходят обкатку при неполной мощности.

В результате обкатки происходит первичный износ поверхности (сглаживание микронеровностей), происходит приработка поверхностей («притирка» поверхностей одна к другой). Только после этого машина может использоваться на полную мощность.

 

Трение в пятах

 

 

Первая гипотеза. Так как в данном случае опорная поверхность является плоскостью, то постоянное удельное давление (рисунок 26а) определяется простым делением осевого усилия на площадь опорного кольца:

Выделим кольцевой элемент поверхности толщиной dρ на расстоянии ρ от центра пяты (рисунок 26в). Элементарная нормальная реакция, действующая на этот элемент, определяется умножением удельного давления на его площадь:

Определим элементарную силу трения и момент от этой силы трения:

 

Проинтегрировав по всей опорной поверхности, получим общий момент трения:

 

Подставив значение q, окончательно получаем:

Вторая гипотеза. Как показывает практика, по истечении времени происходит равномерный износ опорной поверхности пяты, т.е. произведение удельного давления на относительную скорость величина постоянная:

В данном случае скорость в разных точках контактной поверхности различна:

Но так как для вала угловая скорость едина, то износ будет пропорционален произведению q⋅ρ другими словами это произведение является некоторой константой k:

Таким образом, эпюра удельного давления представляет собой гиперболическую зависимость (рисунок 26б). В результате износа поверхности удельное давление перераспределяется таким образом, что при приближении к оси вращения вала оно резко увеличивается (теоретически увеличиваясь до бесконечности в центре опорной поверхности). Именно поэтому сплошные пяты в технике практически не применяются.

Дальнейшее решение ведется аналогично решению по первой гипотезе. В результате получается следующая зависимость для определения момента от сил трения на опорной поверхности пяты:

В полученном виде сложно сравнивать гипотезы между собой. Поэтому для оценки результатов рассматривают сплошные пяты (d=0):

Сравнение показывает, что приработкой поверхностей пяты достигается эффект, аналогичный тому, который имеет место в цапфах – величина сил трения уменьшается на 20…25%

 

Трение гибких тел

 

Гибкие ленты, ремни, канаты и другие подобные материалы, оказывающие малое сопротивление при изгибе получили широкое применение в машинах в виде ременных и канатных приводов, а также в механизмах грузоподъемных машин, в ленточных тормозах.

При определении силы трения между барабаном и гибкой нитью (лентой) принимается следующее допущение – нить абсолютно гибкая и нерастяжимая. При таком допущении пренебрегают усилиями, затрачиваемыми на де