Аналитический метод кинематического исследования

 

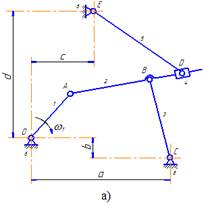
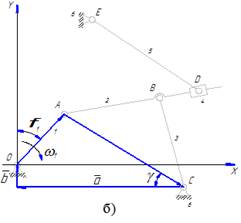
При этом методе звенья механизма, его характерные размеры и перемещения звеньев представляются в виде векторов. В результате формируются векторные многоугольники, на основании которых составляются векторные уравнения. Рассматривая эти векторные уравнения в проекциях на оси произвольно выбранной системы координат, получают системы алгебраических уравнений, решая которые выводят уравнения для определения перемещений (линейных или угловых) исследуемых звеньев.

В качестве параметра выступает обобщенная координата начального звена (обычно угол поворота входного кривошипа). Задавая различные значения обобщенной координаты, по полученным уравнениям определяют положения исследуемых звеньев в различных положениях механизма. Двойным дифференцированием уравнений перемещений получают уравнения для определения скоростей (линейных или угловых) и ускорений (линейных или угловых) исследуемых звеньев.

Однако, как показывает практика, уравнения скоростей и ускорений даже для простых механизмов получаются весьма громоздкими, с большой вероятностью получения ошибок при многоступенчатом дифференцировании. Кроме того такой подход требует отдельного программирования для каждого механизма при использовании ЭВМ. Поэтому (как было показано выше) удобно использовать аналитический метод в комбинации с графическим методом в качестве алгоритма машинного решения задачи. Такой подход делает решение задачи весьма рациональным.

Особенностью групп Ассура II класса 1-го и 2-го видов является то, что с геометрической точки зрения они имеют два решения. Поэтому применение общего принципа составления аналитических уравнений, изложенного выше, приводит к решению сложных квадратных уравнений, имеющих два корня.

Возникает новая задача по выявлению того корня, который соответствует заданному механизму. Для упрощения решения задачи надо воспользоваться следующими рекомендациями:

- в группе 1-го вида при составлении векторного многоугольника необходимо «двигаться» от одного крайнего шарнира к другому, а не по звеньям группы;

- в группе 2-го вида при составлении суммы проекций необходимо провести вспомогательную ось перпендикулярно направляющей, по которой движется ползун, и рассмотреть построенный векторный многоугольник в проекции на эту ось.

Изображенный на рисунке 11 механизм содержит оба эти случая. При формировании векторного многоугольника для первой части этого механизма, включающей группу Ассура второго класса первого вида, проведен вектор AC, соединяющий крайние шарниры A и C данной группы (рисунок 11б).

В результате определяются угол γ и размер AC, после чего в треугольнике ABC становятся известными все три стороны. По теореме косинусов можно определить любой из углов этого треугольника. В данном случае определяется угол α (рисунок 11в), т.к. для дальнейшего решения задачи необходимо знать угол φ2.

 

 

Векторный многоугольник, включающий группу второго класса второго вида, рассматривается в проекции на ось Y1, проведенной перпендикулярно направляющей ABD (рисунок 11в). Полученное алгебраическое уравнение позволяет определить угол β и далее искомый угол φ5.

Конкретно аналитическое определение углового перемещения выходного звена 5, представленного на рисунке 11 механизма (с учетом изложенных выше рекомендаций), будет иметь следующий вид:

 

 

 

По этим уравнениям с помощью ЭВМ определяется угловое перемещение выходного звена φ5 в рад, угловая скорость ω5 в рад/с, угловое ускорение ε5 в рад/с2 для “n” положений механизма.

 

Динамика механизмов и машин

Задачи динамики

 

В данном разделе изучается движение звеньев механизма с учетом действующих на них сил. При этом рассматриваются следующие основные задачи динамики:

1) изучение сил, действующих на звенья механизма, и определение неизвестных сил при заданном законе движения на входе;

2) задача об энергетическом балансе машины;

3) установление истинного закона движения под действием заданных сил;

4) регулирование хода машины;

5) уравновешивание сил инерции;

6) динамика приводов.

 

Силовой расчет механизмов

 

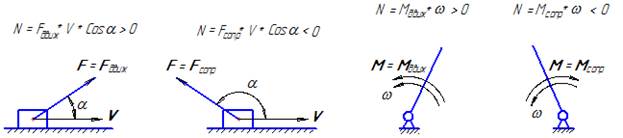
Силовой расчет механизмов относится к решению первой задачи динамики. Как видно из содержания задач динамики, приведенного выше, первая задача включает в себя две части: изучение сил, действующих на звенья механизма; определение неизвестных сил при заданном законе движения на входе (эта вторая часть и есть задача силового расчета).

В целях дальнейшего понимания терминологии и систематизации материала целесообразно повторить известные из физики и теоретической механики сведения о силах, а также ввести некоторые новые (применяемые в теории механизмов и машин) понятия. С точки зрения решения задач динамики силы (в данном случае под силой понимается обобщенное понятие силового фактора – собственно сила или момент) можно классифицировать следующим образом:

а) по взаимодействию звена механизма с другими объектами. По этому признаку силы подразделяются на внешние и внутренние:

- внешние силы – это силы взаимодействия звена механизма с какими-то телами или полями, не входящими в состав механизма;

- внутренние силы – это силы взаимодействия между звеньями механизма (реакции в кинематических парах);

- движущая сила – это сила, которая помогает движению звена и развивает положительную мощность;

б) по мощности, развиваемой силой. По этому признаку силы делятся на силы движущие и силы сопротивления (рисунок 16):

- сила сопротивления препятствует движению звена и развивает отрицательную мощность.

 

 

В свою очередь силы сопротивления можно разделить на силы полезного сопротивления и силы вредного сопротивления:

- силы полезного сопротивления – это силы, для преодоления которых и создан механизм. Преодолевая силы полезного сопротивления, механизм создает полезную работу (например, преодолевая сопротивления резанию на станке, добиваются необходимого изменения формы детали; или, преодолевая сопротивление воздуха в компрессоре, сжимают его до требуемого давления и т.д.);

- силы вредного сопротивления – это силы, на преодоление которых затрачивается мощность и эта мощность теряется безвозвратно. Обычно в качестве вредных сил сопротивления выступают силы трения, гидравлического и аэродинамического сопротивлений. Работа по преодолению этих сил переводится в тепло и рассеивается в пространство, поэтому коэффициент полезного действия любого механизма всегда меньше единицы;

в) силы веса – это силы взаимодействия звеньев механизма с гравитационным полем земли;

г) силы трения – силы, сопротивляющиеся относительному перемещению соприкасающихся поверхностей;

д) силы инерции – силы, возникающие при неравномерном движении звена и сопротивляющиеся его ускорению (замедлению). Сила инерции действует на то тело, которое заставляет ускоряться (замедляться) данное звено. В общем случае при неравномерном движении возникает сила инерции и момент сил инерции:

Fин=-m. as, Mин=-Is. e,

где

Fин – главный вектор сил инерции, приложенный в центре масс звена;

Mин – главный момент сил инерции;

m – масса звена;

Is – момент инерции звена относительно центра масс;

as – ускорение центра масс звена;

e – угловое ускорение звена.

Знак минус в формулах показывает, что сила инерции направлена противоположно ускорению центра масс звена, а момент сил инерции направлен противоположно угловому ускорению звена. Знак силы или момента учитывается только при установлении истинного направления силы или момента на расчетной схеме, а в аналитических вычислениях используется абсолютные их значения.

 

 

При силовом анализе механизмов могут встретиться различные случаи, когда один или оба силовых инерционных фактора могут иметь нулевое значение. На рисунке 17, приведенном выше, показаны некоторые случаи возникновения сил и моментов сил инерции при движении звеньев механизма.

Непосредственно силовой расчет сводится к определению неизвестных сил, действующих на звенья механизма. Как известно из теоретической механики для определения неизвестных сил используются уравнения статики.

Механизм же является неравновесной системой, т.к. большинство его звеньев имеет неравномерное движение, а точки, принадлежащие этим звеньям, движутся по сложным криволинейным траекториям (напомним: состояние равновесия – это состояние покоя или прямолинейного равномерного движения).

 

Поэтому для решения поставленной задачи применяется метод кинетостатики. Метод кинетостатики основан на принципе Даламбера: если ко всем внешним силам, действующим на звенья механизма, добавить силы инерции и моменты сил инерции, то данный механизм будет находиться в состоянии статического равновесия. То есть это искусственный прием, приводящий неравновесную систему в состояние равновесия.

Искусственность приема заключается в том, что силы инерции прикладываются не к тем телам, которые заставляют двигаться звенья ускоренно (замедленно), а к самим звеньям.

Применив этот прием, в дальнейшем можно производить силовой расчет с использованием уравнений статики. Однако, чтобы решить задачу с помощью только уравнений равновесия, система должна быть статически определимой.

Условие статической определимости плоской кинематической цепи:

Для каждого звена, расположенного в плоскости, можно составить три независимых уравнения статики. Если в кинематической цепи имеется "n" подвижных звеньев, то в совокупности для этой цепи можно записать 3n независимых уравнений статики (равновесия). Эти уравнения используются для определения реакций в кинематических парах и неизвестных внешних сил.

На плоскости существуют кинематические пары только пятого и четвертого классов. Пары пятого класса представлены вращательной кинематической парой (шарниром) и поступательной парой (соединение ползуна с направляющей). В шарнире усилие между звеньями может передаваться в любом направлении, поэтому у реакции в шарнире неизвестными являются величина и направление (два компонента), т.е. для определения полной реакции во вращательной паре надо затратить два уравнения статики.

В первом приближении расчет ведется без учета сил трения. В этом случае перемещению ползуна вдоль направляющей ничто не препятствует. Перемещаться же поперек направляющей и поворачиваться ползун не может, поэтому в поступательной паре реакция направлена перпендикулярно направляющей и возникает реактивный момент, препятствующий повороту ползуна.

При силовом расчете обычно реактивный момент не определяют, а находят условную точку приложения реакции (произведение реакции на расстояние до ее условной точки приложения и есть реактивный момент). На определение реакции в поступательной паре также надо затратить два уравнения статики (определить два компонента – величину и точку приложения). Таким образом, на определение полной реакции в кинематической паре пятого класса необходимо затратить два уравнения статики.

Пары четвертого класса (высшие пары) на плоскости представляют соприкасающиеся между собой профили. В высшей паре усилие между звеньями передается по общей нормали к касающимся профилям (без учета сил трения). Поэтому в высшей паре четвертого класса реакция неизвестна только по величине (точка приложения реакции в точке контакта профилей, направление вдоль общей нормали к этим профилям).

Таким образом, для определения реакции в паре четвертого класса надо затратить одно уравнение статики (определить один компонент – величину реакции).

Если в кинематической цепи количество пар пятого класса равно Р5, то на определение реакций во всех этих парах надо затратить 2Р5 уравнений статики. На определение реакций во всех парах четвертого класса используется число уравнений, равное количеству этих пар Р4.

Таким образом, из 3n независимых уравнений статики 2Р5 уравнений используются для определения реакций в парах пятого класса и Р4 – для определения реакций в парах четвертого класса. Оставшиеся уравнения используются для определения неизвестных внешних сил, действующих на звенья механизма.

Пусть X – число уравнений, оставшихся для определения неизвестных внешних сил, тогда

X=3n–2Р5–Р4,

но эта формула совпадает с формулой Чебышева для определения числа степеней свободы плоской кинематической цепи. В результате можно сформулировать условие статической определимости кинематической цепи следующим образом: кинематическая цепь статически определима в том случае, когда число неизвестных внешних сил, действующих на ее звенья, не превышает числа степеней свободы этой цепи.

Так как методы решения разработаны для групп Ассура, то необходимо сформулировать условие статической определимости группы Ассура. Группа Ассура – это кинематическая цепь, имеющая собственную степень свободы, равную нулю. Поэтому группа Ассура статически определима, если на ее звенья не действуют неизвестные внешние силы. Уравнений в группе Ассура достаточно лишь для определения реакций в кинематических парах. Это обстоятельство предопределяет порядок силового расчета механизма:

- разбивают механизм на группы Ассура, взяв в качестве начального то звено, на которое действует неизвестная внешняя сила;

- решение начинают с последней присоединенной группы и заканчивают начальным звеном.

При таком подходе на группы Ассура всегда будут действовать только известные внешние силы и из рассмотрения их равновесия будут определены реакции в кинематических парах, а из рассмотрения условий равновесия начальных звеньев будут определены оставшиеся реакции и неизвестные внешние силы.

Поскольку решение ведется по группам Ассура, то ниже рассматривается принцип силового расчета групп на примере групп второго класса.