
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамический анализ механизмовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Основная задача динамического анализа состоит в определении управляющего силового воздействия - уравновешивающей силы или уравновешивающего момента, приложенного к кривошипу. Эти силовые факторы являются функциями положения кривошипа и в данный момент обеспечивают движение звеньев механизма по заданному закону и уравновешивание механизма. Дополнительной задачей динамического анализа механизмов является определение реакций в кинематических парах. Знание этих сил необходимо при расчете звеньев механизма на прочность, жесткость, износостойкость, виброустойчивость и других расчетах при проектировании механизмов. Для проведения динамического исследования применяется метод кинетостатики, основанный на принципе Д,Аламбера, применительно к механизмам сущность этого метода можно сформулировать так: «Если ко всем внешним, действующим на звено механизма, силам присоединить силы инерции, то под действием всех этих сил звено можно рассматривать условно находящимся в равновесии». Силовой расчет с применением принципа Д,Аламбера называется кинетостатическим. Определение сил и моментов инерции звеньев Изучение сил и моментов инерции, действующих на звено механизма, ведут в зависимости от характера движения звена. Общий случай. Звено АВ совершает плоскопараллельное движение (рис. 10). Все точки звена совершают движения с различными по величине и направлению ускорениями. Соответственно этому к каждой материальной точке звена может быть приложена присущая ей элементарная сила инерции:
Как известно из теоретической механики, все эти элементарные силы инерции могут быть сведены к главному вектору сил инерции
где т — масса звена, кг; Знаки минус в формулах указывают на то, что главный вектор и главный момент сил инерции направлены в стороны, противоположные направлениям соответствующих ускорений.
Рис. 10 Частные случаи. 1. Звено совершает вращательное движение вокруг оси, не проходящей через центр тяжести (рис. 11). Здесь аналогично все элементарные силы инерции приводятся к главному вектору сил инерции Рис. 11 Рис. 12
2. Звено вращается вокруг оси, проходящей через центр тяжести его (рис 12), например ротор электродвигателя. В этом случае 3. Звено совершает поступательное движение (рис. 13) с ускорением as > 0. Считая, что масса звена сосредоточена в центре тяжести S, главный вектор сил инерции выразится так:
Рис. 13
3.2 Кинетостатический расчет механизмов методом планов сил Кинетостатический расчет механизмов ведется по структурным группам, так как они обладают нулевой подвижностью и являются статически определимыми системами. Для структурной группы принципД,Аламбера можно сформулировать так: «Если ко всем действующим на звенья группы внешним силам присоединить силы инерции и реакции связей, то под действием всех этих сил структурную группу можно условно рассматривать находящейся в равновесии». Кинетостатический расчет начинается с расчета структурной группы, наиболее удаленной от входного звена, и заканчивается расчетом кривошипа. При выполнении кинетостатического расчета механизма должна быть задана кинематическая схема механизма и проведен полный кинематический анализ. Кроме того, должны быть заданы массы звеньев и внешние силы, действующие на механизм. Эти силы можно условно разбить на группы: 1. Движущие силы 2. Силы 3. Силы тяжести звеньев. Пример 7. Произвести кинетостатический расчет механизма (рис. 4) в положении, определяемом углом массы звеньев: моменты инерции звеньев:
Рис. 14 Решение. Составим схему нагружения механизма внешними силами и силами инерции (рис. 15). 1. Определим силы тяжести по величине:
Векторы сил тяжести
Схема нагружения механизма
Рис. 15
2. Определим величины и направления сил и моментов инерции, приложенных к звеньям механизма, для этого воспользуемся планом ускорений из примера 5 (рис. 7). По условию задачи звено О1А вращается с постоянной угловой скоростью, и центр тяжести звена совпадает с осью вращения (т. к. положение центра тяжести
Звено АВ (шатун) совершает плоскопараллельное движение, при этом возникают сила инерции
направленная противоположно ускорению as2 центра тяжести и приложенная в точке S2, и момент инерции
направленный противоположно угловому ускорению Для удобства силового расчета механизма момент инерции
Полученная пара сил заменяет действие момента инерции Звено О2В (коромысло) совершает возвратно-вращательное движение, в этом случае также имеет место сила инерции
Силу Момент инерции:
Заменяем Ми3 эквивалентной парой сил на плече О2В (рис. 15). Определяем величины сил пары:
Звено DE (шатун) совершает плоскопараллельное движение. Определяем возникающие при его движении силу инерции и момент инерции:
Силу инерции Ри4 прикладываем в точке S4 в сторону, противоположную ускорению as4, момент инерции заменяем эквивалентной парой сил:
Силу Звено 5 (ползун) совершает поступательное движение вдоль неподвижной направляющей. В этом случае возникает только сила инерции
направленная противоположно ускорению aЕ центра тяжести звена 5. 3. Сила производственного сопротивления Рп.с. приложена к ползуну в точке Е и направлена противоположно вектору скорости VE точки Е. Для определениявеличины этой силы в заданном положении механизма построим график зависимости Рп.с. = Рп.с. (SE) (рис. 16). По оси абсцисс отложим отрезок Е0Еm, соответствующий максимальному перемещению ползуна. Если этот отрезок измерить непосредственно по планам положений (рис. 4), то масштабный коэффициент
Рис. 16 4. Определим реакции в кинематических парах. Механизм состоит из первичного механизма I класса и двух двухповодковых структурных групп. II класса 4 —5 и 2 — 3 (см. рис. 2). Силовой расчет механизма начинаем с наиболее удаленной от ведущего звена группы 4 —5, состоящей из звеньев 4 и 5, двух вращательных пар D и E и одной крайней поступательной пары F. Эту группу вычерчиваем отдельно в том же масштабе, что и схема механизма (рис. 17). На группу 4 —5 действуют известные по величине и направлению силы G4, C5,
Рис. 17
Рис. 18
другую
Поскольку это уравнение решается путем построения плана сил, то силы Реакцию
откуда
Здесь длины отрезков hP Для построения плана сил, исходя из величин сил, входящих в уравнение (3.1), задаемся масштабом плана
От произвольной точки а — полюса плана сил (рис. 18) параллельно силе
Вектор
Чтобы определить реакции в кинематической паре Е, составляем уравнение равновесия сил, действующих на звено 4:
где Векторы сил
Реакция
Переходим к расчету группы 2 — 3, состоящей из звеньев 2 и 3 и из трех вращательных пар А, В и 02. На группу 2 — 3 действуют известные по величине и направлению силы G2, G3, Для определения реакции
откуда Знак «минус» показывает, что действительное направление реакции Для определения реакции
откуда
Знак «плюс» показывает, что выбранное направление реакции
Рис. 19
Рис.20
Для определения реакций в кинематических парах А и 02 построим план сил для двухповодковой группы 2 — 3 в целом согласно векторному уравнению
Силы Из плана сил определяем величины и направления сил
Чтобы определить реакции в кинематической паре В, составляем уравнение равновесия сил, действующих на звено 2 (отбросив звено 3, а действие его на звено 2 выразив реакцией
Согласно плану сил реакцию
Реакция
Производим расчет ведущего звена. На кривошип О1А действуют: со стороны звена 2 реакция Вначале определяем величинy силы
откуда Реакцию
Масштаб плана сил принимаем
Рис. 21
Рис. 22 Из плана Полученные искомые величины реакций и уравновешивающей силы в соответствующих кинематических парах вносим в таблицу 5: Таблица 5
3.3 Определение уравновешивающей силы методом Жуковского Уравновешивающую силу, приложенную к ведущему звену механизма, можно определить на основании теоремы Н. Е. Жуковского о жестком рычаге, суть которой заключается в следующем: «Если какой-либо механизм с одной степенью подвижности под действием внешних сил, находится в равновесии, то в равновесии находится и повернутый на 90° план скоростей этого механизма, рассматриваемый как жесткий рычаг, вращающийся вокруг полюса р, и нагруженный теми же силами, приложенными в одноименных точках». План скоростей, повернутый на 90°, с приложенными к нему внешними силами и силами инерции называют рычагом Жуковского. Пример 8. Определить уравновешивающую силу, приложенную в точке А кривошипа О1А методом Н.Е. Жуковского для механизма, изображенного на рис. 15. Значения внешних сил и сил инерции взять из примера 7. Решение. Строим в произвольном масштабе повернутый на 90° план скоростей механизма (рис. 23). Для удобства принимаем масштаб В точке а планаперпендикулярно к вектору pa прикладываем силу Составляем уравнение моментов всех перенесенных на план скоростей сил относительно полюса р:
откуда:
где длины плеч измеряем на чертеже в миллиметрах. Так как численное значение уравновешивающей силы Сравним величины уравновешивающих сил, полученных силовым расчетом механизма (
Относительная погрешность в вычислениях не превысила допустимой.
Рис. 23 Вопросы для самоконтроля. 1. Три этапа анализа механизмов и машин. 2. Задачи структурного анализа рычажных механизмов с низшими кинематическими парами по Ассуру. 3. Подвижность механизма. Формула Чебышева для определения подвижности плоского механизма. 4. Первичный механизм и группы Ассура. Класс и порядок механизма. 5. Задачи кинематического анализа механизма. Кинематические характеристики передаточные функции (аналоги скоростей и ускорений) механизма. 6. Кинематический анализ рычажных механизмов методом планов положений. 7. Кинематический анализ рычажных механизмов методом векторных уравнений и их графическое решение в форме планов скоростей и ускорений. 8. Прямая и обратная задачи динамики. 9. Динамические параметры механизма. 10. Силы, действующие в механизмах и их классификация. 11. Силы в кинематических парах без учета трения. 12. Инерционная нагрузка звеньев механизма. 13. Задачи, метод и последовательность кинетостатического анализа. 14. Кинетостатический расчет графоаналитическим методом планов сил. 15. Уравновешивающая сила (момент) и ее расчет по Жуковскому Н.Е.
Литература 1. Артоболевский И.И. Теория механизмов и машин. М.: Наука, 1975. 638 с. 2. Иванов М. Е, Павленко В.С. Теория механизмов и машин. Решение задач по структуре, кинематике и кинетостатике плоских рычажных механизмов. Киев:«Вища школа», 1977. 48 с. 3. Курсовое проектирование по теории механизмов и машин /Кореняко А.С. и др./ под ред. А.С. Кореняко. Изд. 5-е.: Киев: «Вища школа», 1970. 330 с. 4. Матвеев Ю.А., Матвеева Л.В. Теория механизмов и машин: Учебное пособие.- М.: Альфа-М: ИНФРА-М, 2009. 320 с. 5. Махова Н.С., Поболь О.Н., Семин М.И. Основы теории механизмов и машин: учебное пособие для технических вузов. М: Гуманитар. изд. центр ВЛАДОС, 2006. – 287 с. 6. Теория механизмов и машин: Учебник для втузов /К.В. Фролов, С.А. Попов, А.К. Мусатов и др. / Под ред. К.В. Фролова. Изд. 5-е М.: Высш. шк., 2005. 496 с.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.209 (0.04 с.) |


 , приложенному в центре тяжести S звена и к главному моменту сил инерции
, приложенному в центре тяжести S звена и к главному моменту сил инерции  , которые соответственно выражаются формулами:
, которые соответственно выражаются формулами:
 — ускорение центра тяжести, м/с2;
— ускорение центра тяжести, м/с2;  — момент инерции звена относительно оси, проходящей через центр тяжести, кгм2;
— момент инерции звена относительно оси, проходящей через центр тяжести, кгм2;  — угловое ускорение звена, 1/с2.
— угловое ускорение звена, 1/с2.

 , (H) и к главному моменту сил инерции
, (H) и к главному моменту сил инерции  (Нм). Если звено вращается равномерно (
(Нм). Если звено вращается равномерно ( = 0), то
= 0), то  = 0, а ускорение центра масс будет равно нормальной составляющей
= 0, а ускорение центра масс будет равно нормальной составляющей  , тогда
, тогда  =
=  .
. 

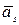 = 0 следовательно главный вектор сил инерции
= 0 следовательно главный вектор сил инерции  = 0. Если угловое ускорение
= 0. Если угловое ускорение  , то к звену прикладывается только главный момент сил инерции
, то к звену прикладывается только главный момент сил инерции 
 . Поскольку угловое ускорение ε = 0, то главный момент сил инерции Ми = 0.
. Поскольку угловое ускорение ε = 0, то главный момент сил инерции Ми = 0.
 и движущие моменты
и движущие моменты 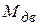 - они же являются уравновешивающими; их требуется определить.
- они же являются уравновешивающими; их требуется определить. и моменты
и моменты  полезного (производственного) сопротивления – они приложены к выходному звену.
полезного (производственного) сопротивления – они приложены к выходному звену. 1 поворота ведущего звена О1A, если, к ползуну (звено 5) приложена сила полезного сопротивления
1 поворота ведущего звена О1A, если, к ползуну (звено 5) приложена сила полезного сопротивления 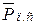 , график изменения которой показан на рис. 14,
, график изменения которой показан на рис. 14,  = 140 Н; уравновешивающая сила
= 140 Н; уравновешивающая сила  у приложена в точке А звена 01А перпендикулярно к оси звена. Размеры звеньев берем по условию примера 5,
у приложена в точке А звена 01А перпендикулярно к оси звена. Размеры звеньев берем по условию примера 5,  = 55°, частота вращения кривошипа п1 =120 об/мин в направлении часовой стрелки;
= 55°, частота вращения кривошипа п1 =120 об/мин в направлении часовой стрелки;


 ;
; = 0,00094 кгм2,
= 0,00094 кгм2,  = 0,00084 кг-м2,
= 0,00084 кг-м2,  = 0,00575 кг-м2.
= 0,00575 кг-м2.
 ,
, 
 ,
,  .
. ,
,  ,
,  ,
,  направлены вертикально вниз и приложены в точках центров масс звеньев S2, S3, S4, S5.
направлены вертикально вниз и приложены в точках центров масс звеньев S2, S3, S4, S5. μl=0,01[м/мм]
μl=0,01[м/мм]
 не задано), поэтому инерционная нагрузка этого звена будет равна нулю:
не задано), поэтому инерционная нагрузка этого звена будет равна нулю: ,
, .
. Н,
Н,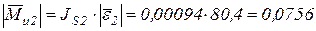 Н·м,
Н·м,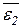 звена АВ.
звена АВ. представляем эквивалентной парой сил, направление вращения которой совпадает с направлением момента. Плечо пары сил принимаем равным длине звена АВ. В точке А перпендикулярно к оси звена АВ прикладываем силу
представляем эквивалентной парой сил, направление вращения которой совпадает с направлением момента. Плечо пары сил принимаем равным длине звена АВ. В точке А перпендикулярно к оси звена АВ прикладываем силу 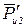 вверх, в точке В перпендикулярно к оси звена АВ прикладываем силу
вверх, в точке В перпендикулярно к оси звена АВ прикладываем силу  , вниз (рис. 15). Сила
, вниз (рис. 15). Сила Н.
Н. - поэтому в дальнейшем расчете его учитывать не будем, а будем учитывать пару сил
- поэтому в дальнейшем расчете его учитывать не будем, а будем учитывать пару сил  и
и  на плече АВ.
на плече АВ. , и момент
, и момент  . Определяем силу инерции:
. Определяем силу инерции: Н.
Н. прикладываем к точке S3 в сторону, противоположную ускорению центра тяжести as3.
прикладываем к точке S3 в сторону, противоположную ускорению центра тяжести as3. Н·м.
Н·м. Н.
Н. Н.
Н. Н·м.
Н·м. Н.
Н. прикладываем к точке Е вниз перпендикулярно к оси звена DE, силу
прикладываем к точке Е вниз перпендикулярно к оси звена DE, силу  — в точке D вверх (рис. 15).
— в точке D вверх (рис. 15). Н,
Н, будет тот же. По оси ординат отложим значения силы сопротивления в произвольно выбранном масштабе
будет тот же. По оси ординат отложим значения силы сопротивления в произвольно выбранном масштабе  . На отрезке Е0Еm отметим заданное положение ползуна - точку Е. Так как это положение механизма соответствует рабочему ходу (ползун удаляется от кривошипа О1А), то значение силы сопротивления Рп.с. равно максимальному 140 Н.
. На отрезке Е0Еm отметим заданное положение ползуна - точку Е. Так как это положение механизма соответствует рабочему ходу (ползун удаляется от кривошипа О1А), то значение силы сопротивления Рп.с. равно максимальному 140 Н.
 ,
,  ,
,  ,
,  и Рп с. Освобождаем группу 4—5 от связей и прикладываем вместо них две реакции: одну реакцию
и Рп с. Освобождаем группу 4—5 от связей и прикладываем вместо них две реакции: одну реакцию  — в поступательной паре Е, перпендикулярную к направляющей ползуна и неизвестную по величине (направление R05 принимается перпендикулярным к направляющей в условиях, когда силы трения не учитываются);
— в поступательной паре Е, перпендикулярную к направляющей ползуна и неизвестную по величине (направление R05 принимается перпендикулярным к направляющей в условиях, когда силы трения не учитываются);


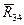 — в шарнире D, неизвестную по величине и направлению. Реакцию
— в шарнире D, неизвестную по величине и направлению. Реакцию  , направленной перпендикулярно к оси звена DE, и нормальной
, направленной перпендикулярно к оси звена DE, и нормальной  , направленной вдоль звена DE. Направлением составляющих задаемся произвольно, как показано пунктирными векторами на рис. 17. Чтобы определить реакции в кинематических парах D и F, составляем векторное уравнение равновесия сил, действующих на группу 4—5, причем сначала в уравнение записываем все силы, действующие на звено 4, затем на звено 5:
, направленной вдоль звена DE. Направлением составляющих задаемся произвольно, как показано пунктирными векторами на рис. 17. Чтобы определить реакции в кинематических парах D и F, составляем векторное уравнение равновесия сил, действующих на группу 4—5, причем сначала в уравнение записываем все силы, действующие на звено 4, затем на звено 5: (3.1)
(3.1) , входящую в уравнение, можно определить аналитически, - для этого составляем уравнение моментов всех сил, действующих на звено DE, относительно точки Е:
, входящую в уравнение, можно определить аналитически, - для этого составляем уравнение моментов всех сил, действующих на звено DE, относительно точки Е: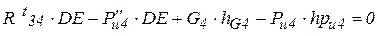 ,
,
 , hG
, hG  и DE взяты в миллиметрах из чертежа. Поскольку составляющая
и DE взяты в миллиметрах из чертежа. Поскольку составляющая  получилась со знаком минус, то это значит, что ее действительное направление противоположно выбранному.
получилась со знаком минус, то это значит, что ее действительное направление противоположно выбранному. = 2 Н/мм и вычисляем длины векторов, изображающих известные силы:
= 2 Н/мм и вычисляем длины векторов, изображающих известные силы: мм;
мм;  мм;
мм; мм;
мм;  мм;
мм; мм;
мм;  мм.
мм. откладываем в том же направлении вектор be. Далее откладываем последовательно векторы: cd силы G4, de силы РИ5, ef силы G5, fq силы Рп. с. Через точку а плана сил параллельно звену DE проводим линию действия силы
откладываем в том же направлении вектор be. Далее откладываем последовательно векторы: cd силы G4, de силы РИ5, ef силы G5, fq силы Рп. с. Через точку а плана сил параллельно звену DE проводим линию действия силы  , а через точку q перпендикулярно к направляющей ползуна — линию действия силы
, а через точку q перпендикулярно к направляющей ползуна — линию действия силы  и ha силы
и ha силы  Н;
Н; Н.
Н. , являясь геометрической суммой векторов ha и ab, представляет в масштабе
, являясь геометрической суммой векторов ha и ab, представляет в масштабе  :
: Н.
Н. ,
, — реакция со стороны звена 5 на звено 4.
— реакция со стороны звена 5 на звено 4. (
( ),
),  ) на плане сил (рис. 18)уже имеются, поэтому неизвестная реакция
) на плане сил (рис. 18)уже имеются, поэтому неизвестная реакция  будет представлена замыкающим вектором ah на этом плане:
будет представлена замыкающим вектором ah на этом плане: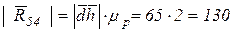 Н.
Н. со стороны звена 4 на звено 5 равна по величине реакции
со стороны звена 4 на звено 5 равна по величине реакции 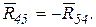
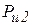 ,
,  = —
= —  ,
,  = —
= —  ,
,  ,
,  — реакция со стороны звена 4 на звено 3, связанная с реакцией
— реакция со стороны звена 4 на звено 3, связанная с реакцией  зависимостью
зависимостью  в шарнире А и
в шарнире А и 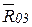 в шарнире 02, неизвестные по величине и направлению. Представляем реакции
в шарнире 02, неизвестные по величине и направлению. Представляем реакции 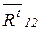 и
и  показаны пунктирными векторами (рис. 19).
показаны пунктирными векторами (рис. 19).
 Н.
Н.

 Н.
Н.

 (3.2)
(3.2) и
и  ,
,  и
и  в уравнение не записываем, так как при построении плана сил они взаимно уравновешиваются. Масштаб плана сил
в уравнение не записываем, так как при построении плана сил они взаимно уравновешиваются. Масштаб плана сил  = 2 Н/мм. Вычисляем длины векторов, изображающих известные силы, входящие в уравнение (3.2) и строим план сил (рис. 20).
= 2 Н/мм. Вычисляем длины векторов, изображающих известные силы, входящие в уравнение (3.2) и строим план сил (рис. 20).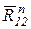 и
и 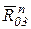 , а также полных реакций
, а также полных реакций  =
= 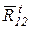 +
+  +
+  Н;
Н; Н;
Н; Н;
Н; Н.
Н. ):
):
 :
: Н.
Н. равна по величине реакции
равна по величине реакции  .
. и со стороны стойки реакция
и со стороны стойки реакция  . Кроме этих сил в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу
. Кроме этих сил в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу  (рис. 21). Сила
(рис. 21). Сила 
 Н.
Н. по величине и направлению определяем путем построения плана сил (рис. 21), действующих на звено 1, согласно векторному уравнению
по величине и направлению определяем путем построения плана сил (рис. 21), действующих на звено 1, согласно векторному уравнению .
. Н/мм.
Н/мм.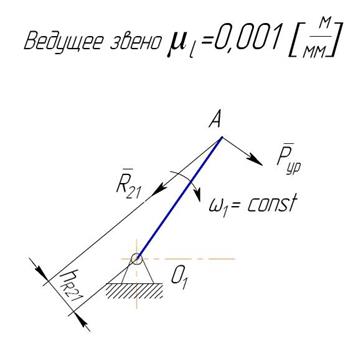


 Н.
Н. ,Н
,Н
 , Н
, Н
 , Н
, Н
 ,Н
,Н
 , Н
, Н
 , Н
, Н
 , Н
, Н
 ,Н
,Н
 = 0,00285 [м/с·мм], при этом длины векторов повернутого плана скоростей увеличатся вдвое по сравнению с векторами построенного ранее плана скоростей. Переносим на этот план заданную силу производственного сопротивления
= 0,00285 [м/с·мм], при этом длины векторов повернутого плана скоростей увеличатся вдвое по сравнению с векторами построенного ранее плана скоростей. Переносим на этот план заданную силу производственного сопротивления  , силы веса G2, G3, G4, G5, силы инерции
, силы веса G2, G3, G4, G5, силы инерции  ,
, 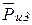 ,
,  ,
,  . Перечисленные силы (рис. 15) переносим параллельно самим себе и прикладываем в одноименных точках повернутого на 90° плана скоростей: силы
. Перечисленные силы (рис. 15) переносим параллельно самим себе и прикладываем в одноименных точках повернутого на 90° плана скоростей: силы  и
и  ,
,  и
и  ,
,  и
и  от моментов инерции
от моментов инерции  ,
,  и
и  также переносим в одноименные точки, но так, чтобы направление вращения пары сил совпадало с направлением соответствующего момента. Так, например, пара сил
также переносим в одноименные точки, но так, чтобы направление вращения пары сил совпадало с направлением соответствующего момента. Так, например, пара сил  и
и  переносим в точки d и e, направление вращения – по часовой стрелке.
переносим в точки d и e, направление вращения – по часовой стрелке. , причем направление выбираем произвольно.
, причем направление выбираем произвольно.

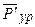 получили положительное, то направление было выбрано верно.
получили положительное, то направление было выбрано верно. ) и с помощью рычага Н.Е. Жуковского (
) и с помощью рычага Н.Е. Жуковского (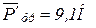 ), и вычислим относительную погрешность, приняв за основу результат, полученный с помощью рычага Жуковского:
), и вычислим относительную погрешность, приняв за основу результат, полученный с помощью рычага Жуковского: ,
,



