
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематический анализ механизмов методом диаграммСодержание книги
Поиск на нашем сайте
С помощью графиков перемещений, скоростей и ускорений какой-либо точки можно проследить изменение кинематических параметров точки за полный цикл движения механизма. Имея один из графиков, путем графического дифференцирования или интегрирования можно получить два остальных, так как между перемещением, скоростью и ускорением точки существует зависимость
т.е. скорость точки в определенный момент времени представляет собой первую производную от перемещения точки по времени, а ускорение – первую производную от скорости по времени. Следовательно, имея график перемещений точки, можно путем дифференцирования его получить график скоростей, а путем дифференцирования графика скоростей – график ускорений. Если исследуется движение точки, совершающей поступательное движение, то для нее строится график линейных перемещений. Если же исследуется движение точки, совершающей вращательное движение, то для нее строится график линейных перемещений (при этом надо очень тщательно измерять перемещение точки по дуге) или график угловых перемещений звена, к которому относится заданная точка. При дифференцировании графика угловых перемещений получится соответственно график угловых скоростей, а при дифференцировании последнего – график угловых ускорений. Известно несколько методов графического дифференцирования. Предпочтительными из них являются метод касательных и метод хорд. Пример 6. Для механизма (рис. 4) построить график перемещений точки Решение. Строим систему координат графика перемещений (рис. 9). По оси ординат будем откладывать перемещение точки
и длине отрезка
Рис. 9
Делим отрезок Перемещение точки Е при движении механизма из нулевого положения в первое выражается отрезком
Однако для того чтобы рационально использовать поле чертежа, т.е. чтобы график был не слишком сжат и не слишком вытянут, удобно задаться максимальной ординатой
где По рис. 4
Из полученной точки Определяем масштаб графика перемещений по формуле
Определяем длины ординат
Из точек 1, 2, 3 и т.д. на оси абсцисс откладываем полученные расчетом ординаты Для построения графика скоростей точки Е Под графиком перемещений точки Е строим новую систему координат для графика скоростей. Влево от начала этой системы координат (точка О) на оси абсцисс произвольно выбираем полюс Далее, на оси ординат точки 1, 2, 3 и т.д. проецируем соответственно на перпендикуляры к оси абсцисс, восстановленные из точек и 1, 2, 3 и т.д. деления отрезка
Из построений следует, что ординаты графика По известной формуле определяем коэффициент пропорциональности – масштаб скоростей:
где
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.83.68 (0.01 с.) |

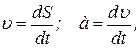
 и, дифференцируя его методом касательных, график скоростей этой точки. Кривошип
и, дифференцируя его методом касательных, график скоростей этой точки. Кривошип  имеет частоту вращения
имеет частоту вращения  об/мин.
об/мин. . При длительности цикла
. При длительности цикла
 , равной 80мм, масштаб времени по оси абсцисс
, равной 80мм, масштаб времени по оси абсцисс

 . Если отрезок
. Если отрезок  перемещений графика совпадает с масштабом
перемещений графика совпадает с масштабом  длин схемы механизма.
длин схемы механизма. . Принимаем эту ординату равной 57 мм. Откладывать ее надо из точки
. Принимаем эту ординату равной 57 мм. Откладывать ее надо из точки  , положение которой на оси абсцисс графика перемещений находим из соотношения
, положение которой на оси абсцисс графика перемещений находим из соотношения ,
, и
и  - длины отрезков на оси абсцисс графика перемещений;
- длины отрезков на оси абсцисс графика перемещений;  и
и  - отрезки траектории точки А, соответствующие переходу механизма из четвертого положение в положении максимального удаления точки В и в пятое положение.
- отрезки траектории точки А, соответствующие переходу механизма из четвертого положение в положении максимального удаления точки В и в пятое положение. = 4мм.
= 4мм.

 и т.д. графика перемещений точки Е, предварительно измерив соответствующие отрезки
и т.д. графика перемещений точки Е, предварительно измерив соответствующие отрезки  и т.д.,:
и т.д.,: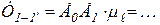 = 4мм;
= 4мм;
 и т.д.
и т.д. и т.д. Полученные точки
и т.д. Полученные точки  и т.д. соединяем плавной кривой (рис. 9, 1) Это и будет график линейных перемещений точки
и т.д. соединяем плавной кривой (рис. 9, 1) Это и будет график линейных перемещений точки 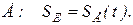
 полученный график продифференцируем методом касательных. С этой целью в точках
полученный график продифференцируем методом касательных. С этой целью в точках  и т.д. к кривой графика
и т.д. к кривой графика  проводим касательные.
проводим касательные. (рис. 9, 2). Из него проводим лучи, параллельные касательным в точках
(рис. 9, 2). Из него проводим лучи, параллельные касательным в точках  и т.д. графика перемещений, до пересечения с осью ординат (скоростей) в точках соответственно 1, 2 и т.д. Отрезки 0-1, 0-2 и т.д. на оси ординат нового графика пропорциональны скоростям точки Е в первом, втором и т.д. положениях механизма.
и т.д. графика перемещений, до пересечения с осью ординат (скоростей) в точках соответственно 1, 2 и т.д. Отрезки 0-1, 0-2 и т.д. на оси ординат нового графика пропорциональны скоростям точки Е в первом, втором и т.д. положениях механизма. пропорциональны значениям скоростей в различных положениях механизма.
пропорциональны значениям скоростей в различных положениях механизма.
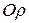 = 13,3 мм – полюсное расстояние (рис 9, 2).
= 13,3 мм – полюсное расстояние (рис 9, 2).


