
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематический анализ механизмовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кинематический анализ механизма состоит в изучении движения звеньев без учета сил, действующих на эти звенья, при заданном движении ведущего звена. Кинематический анализ выполняется по кинематической схеме механизма. Он состоит в определении кинематических характеристик: 1) перемещений звеньев и траекторий, описываемых характерными точками звеньев (например, центра масс звена); 2) линейных скоростей и ускорений точек звеньев; 3) угловых скоростей и ускорений звеньев. Кинематический анализ позволяет установить соответствие кинематических характеристик (перемещений, скоростей и ускорений) заданному закону движения механизма, а также получить исходные данные для выполнения динамического анализа. По полученным кинематическим характеристикам определяют инерционные нагрузки звеньев, кинетическую энергию механизма, закон движения ведущего и ведомых звеньев в функции времени. Кинематическое исследование проводят графическим и аналитическим методами. Графическое определение кинематических параметров основано на геометрических построениях, погрешность результатов которых составляет (0,3-0,5)% по сравнению с аналитическими расчетами. Графический метод нагляден и универсален, так как позволяет определять положения, скорости и ускорения звеньев механизма любой структуры. Метод построения планов положений, скоростей и ускорений применяется при инженерных расчетах, как при анализе, так и при синтезе механизмов. Графический метод построения кинематических диаграмм позволяет использовать при анализе заданные в виде графиков законы изменения кинематических параметров в функции обобщенных координат φ1 и t. 2.1 Построение планов положений Планом положения механизма называется чертеж, изображающий расположение его звеньев в какой-либо определенный момент движения. Отсюда следует, что план положения представляет собой кинематическую схему механизма, вычерченную для заданного положения кривошипа в определенном масштабе. Планы положений механизмов, включающих в себя двухповодковые группы, строятся методом засечек. Пример 2. Построить план положения механизма (рис. 1) для заданного угла поворота φ1 кривошипа при lO Решение. Для построения плана принимаем, что длину кривошипа lO
Затем вычисляем длины остальных отрезков, которые будем откладывать на чертеже:
Построение плана (рис. 3) начинаем с нанесения элементов неподвижного звена. Штрихпунктирной линией проводим линию центров O1O2 и на ней наносим точки O1 и O2 на расстоянии O1O2 = 55 мм. На расстоянии а' от линии O1O2 проводим траекторию движения точки Е. Под углом φ1 = 55° к линии O1O2 через точку О1 проводим ось ведущего звена и от этой точки откладываем на ней отрезок О1А. Это и будет изображение ведущего звена О1A в заданном положении. Положение точки В определяем методом засечек. Для этого из точки А радиусом АВ, а източки O2 радиусом О2B проводим дуги. Точка их пересечения и будет точкой В. На звене O2В находим положение точки D. Сделав радиусом DE из точки D засечку на траектории движения точки Е, определяем положение этой точки на схеме. Положение точки С находим на пересечении дуг радиусов АС и ВС.
Рис. 3 Дополнительно заданы положения центров тяжести:
Используя масштаб длин
Построение траекторий точек Чтобы построить траекторию какой-либо точки, нужно, построить несколько планов положений механизма, найти на каждом из этих планов положение заданной точки и последовательно соединить полученные точки плавной кривой (рис.4). Обычно планы положений механизма строятся для нескольких равноотстоящих положений ведущего звена О1А. Для этого окружность —- траектория точки А — делится на несколько равных частей. Одно из положений точки А принимается за нулевое, а остальные пронумеровываются в направлении вращения звена О1А. За нулевое положение точки А кривошипа выбирают такое, при котором дальнейшее движение точки А в заданную сторону вращения будет соответствовать рабочему ходу исполнительного звена механизма.
Рис. 4 Пример 3. Для механизма по условию примера 1 Решение. Кривошип совершает полное круговое движение и траекторией движения точки А будет окружность радиуса О1А. Проводим эту окружность. Поскольку коромысло 3 совершает качательное движение, то точка В движется по дуге окружности радиуса О2В. Для разметки траектории точки В необходимо на дуге радиуса О2В найти крайние положения точки В. Точка В занимает крайнее левое положение тогда, когда длина О1А кривошипа вычитается из длины АВ шатуна, и крайнее правое,— когда эти длины складываются. Для нахождения крайних положений точки В делаем две засечки из центра О1 радиусами rmin = А В — О1А и r mах = АВ + О1А на дуге радиуса O2B. Получаем точки В0 и Вт. На пересечении прямой В0О1 с окружностью радиуса О1А находим точку А0, а на пересечении прямой ВтО1 с этой окружностью — точку Ат. Два крайних положения О1А0 и О1Ат кривошипа делят его полный оборот (угол 360°) на два неравных по величине угла. Больший из них обычно соответствует рабочему ходу исполнительного звена механизма, меньший — холостому ходу. На рис. 4 эти углы обозначены соответственно φ рх и φ хх. Чтобы при дальнейшем движении в заданную сторону вращения точка А кривошипа двигалась в направлении рабочего хода исполнительного звена механизма, за нулевое положение принимаем крайнее левое положение точки А, обозначенное А0 (рис. 4). Соединяем точки В0 и Вт с точкой 02, находим положения точек D0, Dm, E0, Em и получаем два положения механизма, соответствующие крайним положениям точки В. Чтобы упростить дальнейшее построение, положения точки С не наносим. Разбиваем окружность радиуса О1А, начиная от точки А0, на восемь равных частей (в задании на курсовой проект требуется разбить на двенадцать) и нумеруем точки деления в направлении вращения звена О1А. Используя метод засечек, строим первое, второе и все последующие положения механизма. Определяем длину отрезка
и находим положения точек S20, S2 l, S22 и т. д. Соединяем полученные точки плавной кривой. Это и будет траектория точки S2. 2.3 Построение планов скоростей Зная закон движения ведущего звена и длины всех звеньев механизма, можно определить скорости его точек по величине и направлению в любом положении механизма путем построения плана скоростей для этого положения. Построение планов скоростей и чтение их во многом упрощаются при использовании свойств этих планов, которые заключаются в следующем: 1. Векторы, исходящие из полюса, изображают абсолютные скорости соответствующих точек звеньев механизма в масштабе плана скоростей. Точки плана скоростей, соответствующие неподвижным точкам механизма, находятся в полюсе плана. 2. Векторы, соединяющие концы векторов абсолютных скоростей, выражают величины и направления относительных скоростей. 3. Векторы относительных скоростей точек звена на плане скоростей образуют фигуру, подобную одноименной жесткой фигуре, образованной отрезками, соединяющими эти точки звена на плане механизма, повернутую по отношению к последней на 90° в сторону мгновенного вращения данного звена. Пример 4. Определить абсолютные и относительные скорости точек звеньев и угловые скорости звеньев в восьми положениях механизма (см. рис. 4) методом планов скоростей. Построить годограф скоростей центра масс S2 шатуна 2. Кривошип O1A имеет частоту вращения n1 = 120 об/мин в направлении по часовой стрелке. Размеры звеньев — те же. Решение. Построение плана скоростей рассмотрим на примере одного положения механизма, когда угол поворота кривошипа Определяем угловую скорость кривошипа О1А по формуле:
Из теоретической механики известно, что скорость какой-либо точки звена может быть представлена в виде векторной суммы переносной и относительной скоростей. Тогда абсолютная скорость точки А кривошипа О1А будет определятся
где
Вектор Задаемся длиной отрезка ра, который будет изображать на плане скорость
От произвольной точки р, принятой за полюс плана скоростей, откладываем перпендикулярно к звену О1А отрезок ра (рис. 6). Скорости неподвижных точек О1 и O2 равны нулю, поэтому векторы Для определения скорости точки В воспользуемся векторными уравнениями:
где В этих уравнениях скорость
Направление скорости Согласно уравнению (2.1) вектор
Согласно уравнению (2.2) вектор
Рис. 5
Рис. 6
Рис. 7
Положение точки с (конец вектора скорости точки С) определяем на плане скоростей по теореме подобия (третье свойство планов скоростей). На отрезке ab плана скоростей строим треугольник аbс,подобный треугольнику ABC звена 2. Определяем длины отрезков ас и bc из пропорций
Поскольку АС = ВС, то
Из точек а и b плана скоростей радиусами, равными соответственно отрезкам ас и bc, делаем засечки. Получив две точки пересечения этих дуг, справа и слева от вектора Соединяем полюс плана скоростей р с точкой с и определяем величину скорости
Согласно тому же свойству планов скоростей находим положение точки d на плане исходя из пропорции:
В этом случае фигура относительных скоростей o2db на плане скоростей будет прямой по подобию с прямой О2B механизма:
Определив положение точки d на плане скоростей, находим величину скорости точки D
Скорость точки Е шатуна DE представляем в виде векторной суммы переносной и относительной скоростей. Для ееопределения воспользуемся векторными уравнениями:
где В этих уравнениях скорость
Вектор de определяет величину и направление скорости
Исходя из теоремы подобия (третье свойство планов скоростей) находим на плане точки s2, s3, s4, соответствующие центрам тяжести звеньев S2, S3 и S4. Из полюса р в этиточки проводим векторы. Определяем величины скоростей центров тяжести:
Переходим к определению угловых скоростей звеньев. Угловая скорость ω1 ведущего звена известна по величине и направлению (ω1 = 12,56 1/с и это звено вращается по часовой стрелке). Чтобы определить угловую скорость ω2 звена АВ, рассмотрим вращение точки В вокруг точки А. Направление скорости
При определении направления угловой скорости ω3 поступаем аналогично. Перенесенный в точку В звена O 2 В вектор
Чтобы определить угловую скорость ω4 звена DE, мысленно переносим вектор
Угловая скорость ползуна 5, совершающего прямолинейное поступательное движение, равна нулю. Аналогично строятся планы скоростей для остальных положений механизма. Полученные значения абсолютных и относительных скоростей точек и значения угловых скоростей звеньев для всех положений механизма сводим в таблицу 2. Таблица 2
Для построения годографа скорости центра масс S2 шатуна АВ перенесем со всех планов скоростей векторы скорости Vs2, сохраняя их величину и направление, в общий полюс – произвольно выбранную точку на чертеже (рис. 8). Соединив концы векторов плавной линией, получим годограф скорости т. S2.
Рис. 8
2.4. Построение планов ускорений По аналогии с планами скоростей при помощи планов ускорений можно найти ускорения любых точек механизма. При построении планов ускорений также следует пользоваться их изображающими свойствами, заключающимися в следующем: 1. Векторы, исходящие из полюса, изображают абсолютные ускорения соответствующих точек механизма в масштабе плана ускорений. Точки плана ускорений, соответствующие точкам, ускорения которых равны нулю, располагаются в полюсе. 2. Векторы, соединяющие концы векторов абсолютных ускорений, выражают в том же масштабе полные относительные ускорения. 3. Полные относительные ускорения на плане ускорений образуют фигуру, подобную одноименной жесткой фигуре на плане положения механизма, но повернутую по отношению к последней на некоторый угол 180° —
Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то обычно концы векторов абсолютных ускорений на планах ускорений обозначают буквами, соответствующими названию точек. Концы векторов нормальных составляющих ускорения обозначают другими буквами, не встречающимися в обозначениях точек механизма. Пример 5. Методом планов ускорений определить абсолютные и относительные ускорения точек звеньев и угловые ускорения звеньев для трех положений механизма (рис. 4). Данные взять по условию примера 4. Решение. Построение плана ускорений рассмотрим на том же положении механизма, что в примере 4. Определим ускорение точки А. Поскольку звено O 1 A вращается равномерно
Принимаем длину отрезка р'а', изображающего вектор ускорения
Из произвольной точки р', принятой за полюс плана ускорений, откладываем параллельно звену О 1 А в направлении от точки А кточке О 1 отрезок р'а' (рис. 7). Ускорения точек О 1 и O 2 механизма равны нулю, следовательно, точки о' 1и о 2 будут совпадать с полюсом плана ускорений. Рассматриваем движение точки В со звеньями АВ и BO 2 и по аналогии с планом скоростей составляем векторные уравнения:
Полные относительные ускорения
В этих уравнениях ускорение аА известно по величине и по направлению, ускорение Определяем величины нормальных ускорений:
Ускорение Относительные тангенциальные ускорения известны только по линиям их действия. Ускорение От точки а' плана ускорений параллельно звену АВ в направлении от точки В к точке А откладываем вектор
Через точку п 1проводим перпендикулярно к звену AB линию действия тангенциального ускорения
Через точку п 2 проводим перпендикулярно звену O 2 В линию действия тангенциального ускорения
Точка b' определяет также концы векторов
Вектор
Вектор
Исходя из третьего свойства планов ускорений
Поскольку АС =ВС, то
Из точек а' и b' плана ускорений радиусами, равными соответственно длинам отрезков а'с' и b'с', делаем засечки. Из полученных точек пересечения засекающих дуг (слева и справа от вектора
Находим положение точки d' на плане ускорений исходя из пропорции откуда
Следовательно, абсолютное ускорение точки D
Для определения ускорения точки Е воспользуемся векторными уравнениями:
где а) ускорение б) полное относительное ускорение
где нормальное ускорение
направлено по оси звена DE от точки Е к точке D. Для тангенциального ускорения в) ускорение г) ускорение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 A= 0,03 м; lO
A= 0,03 м; lO  = 0,055 м; lАВ - 0,05 м; l O
= 0,055 м; lАВ - 0,05 м; l O  =0,015 м и угол φ1 = 55°.
=0,015 м и угол φ1 = 55°.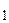 A на схеме будет изображать отрезок O 1 A, длина которого равна 30 мм. Тогда масштаб длин плана
A на схеме будет изображать отрезок O 1 A, длина которого равна 30 мм. Тогда масштаб длин плана м/мм.
м/мм. мм;
мм;  мм;
мм;  мм;
мм; мм;
мм; 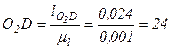 мм;
мм; мм;
мм;  мм.
мм.




 , на плане положений отмечаем центры тяжести:
, на плане положений отмечаем центры тяжести: мм.
мм.  мм.
мм.  мм.
мм.

 , (это положение на рис. 4 выделено).
, (это положение на рис. 4 выделено). 1/c.
1/c.
 - переносная скорость т. О1,
- переносная скорость т. О1,  - относительная скорость т. А во вращении вокруг т. О1. Т. о., абсолютная скорость совпадает с относительной, поэтому скорость точки А находим по формуле
- относительная скорость т. А во вращении вокруг т. О1. Т. о., абсолютная скорость совпадает с относительной, поэтому скорость точки А находим по формуле м/с.
м/с. a направлен перпендикулярно к оси звена O1A в сторону его вращения.
a направлен перпендикулярно к оси звена O1A в сторону его вращения. , точки A; ра = 66 мм. Масштаб плана скоростей
, точки A; ра = 66 мм. Масштаб плана скоростей м/с·мм.
м/с·мм. и
и  также равны нулю и, следовательно, токи о1 и о2 на плане скоростей совпадают с полюсом р.
также равны нулю и, следовательно, токи о1 и о2 на плане скоростей совпадают с полюсом р. (2.1)
(2.1) (2.2)
(2.2) — скорость точки А в переносном движении;
— скорость точки А в переносном движении;  — относительная скорость точки В во вращении вокруг точки А;
— относительная скорость точки В во вращении вокруг точки А;  — скорость точки O 2;
— скорость точки O 2;  — относительная скорость точки В во вращении вокруг точки O 2.
— относительная скорость точки В во вращении вокруг точки O 2. точки В через точку а (конец вектора скорости
точки В через точку а (конец вектора скорости  точки В:
точки В: м/с.
м/с. .
. изображает относительную скорость
изображает относительную скорость  м/с.
м/с. (
( точки В во вращении вокруг точки O 2:
точки В во вращении вокруг точки O 2: м/с.
м/с.



 и
и 
 мм.
мм. ABC звена 2 по направлению вращения часовой стрелки читаем: А
ABC звена 2 по направлению вращения часовой стрелки читаем: А  С
С  точки С:
точки С: м/с.
м/с.
 мм.
мм. м/с.
м/с. (2.3)
(2.3) (2.4)
(2.4) — скорость точки D в переносном движении;
— скорость точки D в переносном движении; 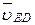 — относительная скорость точки Е во вращении вокруг точки D;
— относительная скорость точки Е во вращении вокруг точки D;  — скорость точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна;
— скорость точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна;  — скорость точки Е в поступательном движении относительно точки Е0.
— скорость точки Е в поступательном движении относительно точки Е0. точки Е. Величина скорости
точки Е. Величина скорости м/с.
м/с. м/с.
м/с. м/с;
м/с; м/с;
м/с; 
 м/с.
м/с. 1/c.
1/c. показывает, что точка В вращается относительно точки O 2 по часовой стрелке. Это определяет направление угловой скорости третьего звена (рис. 5):
показывает, что точка В вращается относительно точки O 2 по часовой стрелке. Это определяет направление угловой скорости третьего звена (рис. 5): 1/с.
1/с. скорости
скорости  1/с.
1/с.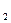 , м/с
, м/с
 , м/с
, м/с
 , м/с
, м/с

 в сторону мгновенного углового ускорения данного звена, где
в сторону мгновенного углового ускорения данного звена, где
 где
где  и
и  , то точка А имеет только нормальное ускорение, которое направлено по звену O 1 A к центру вращения. Величина этого ускорения:
, то точка А имеет только нормальное ускорение, которое направлено по звену O 1 A к центру вращения. Величина этого ускорения: м/с
м/с  .
. точки А, равной 65 мм. Тогда масштаб плана ускорений
точки А, равной 65 мм. Тогда масштаб плана ускорений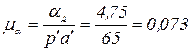 м/с
м/с  мм.
мм. (2.5)
(2.5) (2.6)
(2.6) и
и  , представляем в виде суммы двух составляющих — нормальной, направленной по оси соответствующего звена к центру вращения в относительном движении, и тангенциальной, перпендикулярной к этому звену. Тогда уравнения (2.5) и (2.6) можно записать в следующем виде:
, представляем в виде суммы двух составляющих — нормальной, направленной по оси соответствующего звена к центру вращения в относительном движении, и тангенциальной, перпендикулярной к этому звену. Тогда уравнения (2.5) и (2.6) можно записать в следующем виде:
 = 0.
= 0.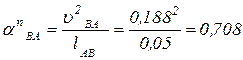 м/с
м/с  м/с
м/с  направлено по оси звена АВ от точки В к точке А, ускорение
направлено по оси звена АВ от точки В к точке А, ускорение  — по оси звена O 2 В от точки В к точке O 2.
— по оси звена O 2 В от точки В к точке O 2. перпендикулярно звену АВ, а ускорение
перпендикулярно звену АВ, а ускорение  перпендикулярно звену O 2 В. Величины и направления тангенциальных ускорений определяем путем построения плана ускорений.
перпендикулярно звену O 2 В. Величины и направления тангенциальных ускорений определяем путем построения плана ускорений. изображающий ускорение
изображающий ускорение  . Длина этого отрезка
. Длина этого отрезка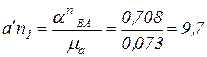 мм.
мм. . Затем от точки о' 2 плана ускорений, совпадающей с полюсом р', параллельно звену O 2 В в направлении от точки В к точке O 2 откладываем вектор
. Затем от точки о' 2 плана ускорений, совпадающей с полюсом р', параллельно звену O 2 В в направлении от точки В к точке O 2 откладываем вектор  , изображающий ускорение
, изображающий ускорение  . Определим длину этого отрезка:
. Определим длину этого отрезка: мм.
мм. . На пересечении линий действия ускорений
. На пересечении линий действия ускорений  получим точку b´ — конец вектора р'b', изображающего ускорение
получим точку b´ — конец вектора р'b', изображающего ускорение  точки В механизма:
точки В механизма: м/с
м/с  и
и  тангенциальных ускорений
тангенциальных ускорений  и
и  :
: м/с
м/с  м/с
м/с  изображает полное относительное ускорение
изображает полное относительное ускорение  точки В во вращении вокруг точки А:
точки В во вращении вокруг точки А: м/с
м/с  полного ускорения
полного ускорения  точки В во вращении относительно точки O 2 механизма совпадает с вектором
точки В во вращении относительно точки O 2 механизма совпадает с вектором  абсолютного ускорения точки В. Следовательно:
абсолютного ускорения точки В. Следовательно: м/с
м/с  а'b'с' - относительных ускорений должен быть подобен
а'b'с' - относительных ускорений должен быть подобен  и
и  .
. мм.
мм. ) в качестве точки с' выбираем точку, расположенную слева, так как при этом порядок букв при обходе треугольника а'b'с' плана ускорений и треугольника ABC механизма будет одинаковым. Соединив полюс плана ускорений с точкой с', получаем вектор абсолютного ускорения точки С механизма:
) в качестве точки с' выбираем точку, расположенную слева, так как при этом порядок букв при обходе треугольника а'b'с' плана ускорений и треугольника ABC механизма будет одинаковым. Соединив полюс плана ускорений с точкой с', получаем вектор абсолютного ускорения точки С механизма: м/с
м/с 
 м/с
м/с  (2.7)
(2.7) (2.8)
(2.8) — абсолютное ускорение точки D;
— абсолютное ускорение точки D;  — полное относительное ускорение точки Е во вращении вокруг точки D;
— полное относительное ускорение точки Е во вращении вокруг точки D;  — ускорение точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна;
— ускорение точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна;  — ускорение точки Е в поступательном движении относительно точки E0. Вэтих уравнениях:
— ускорение точки Е в поступательном движении относительно точки E0. Вэтих уравнениях: и тангенциальной
и тангенциальной  составляющих, тогда уравнение (2.7) принимает вид:
составляющих, тогда уравнение (2.7) принимает вид:
 м/с
м/с 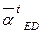 известна только линия его действия, перпендикулярная к звену DE;
известна только линия его действия, перпендикулярная к звену DE; = 0;
= 0;


