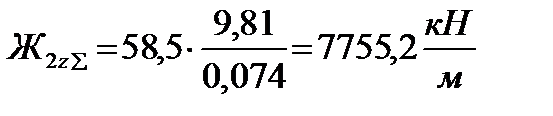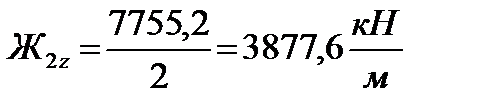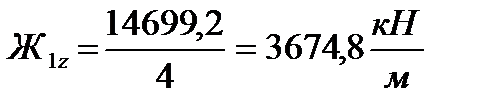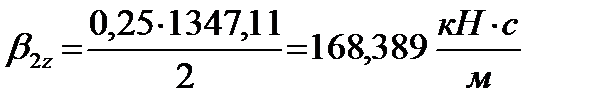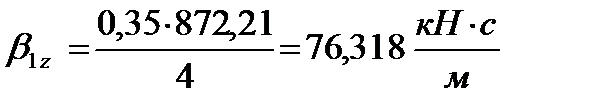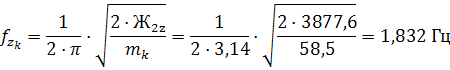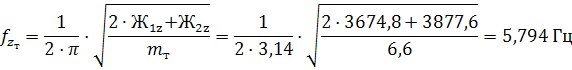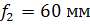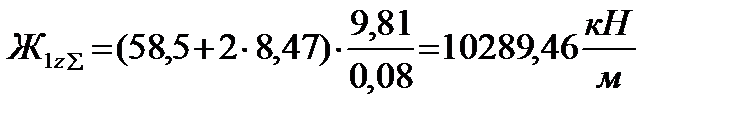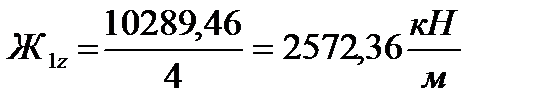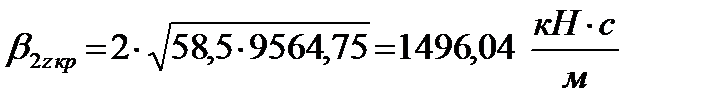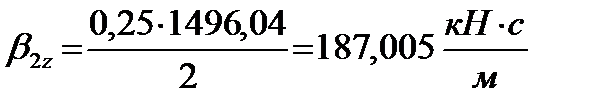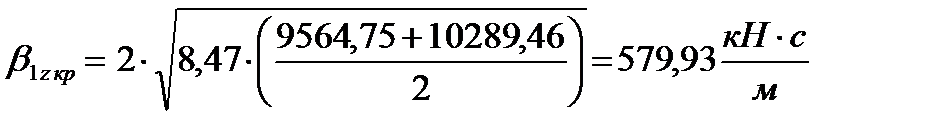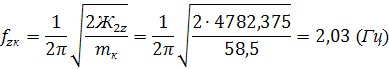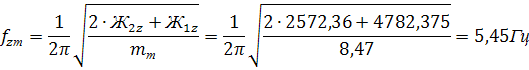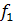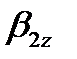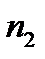Анализ конструкции механической части выбранного для исследования экипажа. Выбор его параметров

Введение

Необходимость повышения скорости движения подвижного состава по рельсовому пути при безусловном обеспечении безопасности в условиях нарастания уровня совместных колебаний пути подвижного состава предъявляет высокие требования к совершенствованию механической части электроподвижного состава (э.п.с.) с точки зрения улучшения его динамических качеств.

В этих условиях исследование колебаний должно являться определяющим при выборе параметров механической части э.п.с. При этом задача исследования заключается в выборе такой системы и параметров рессорного подвешивания, которые обеспечивали бы:

· наилучшие динамические качества экипажа;

· устойчивость движения экипажа в рельсовой колее при выполнении требований к показателям безопасности движения;

· выполнения требований к показателям динамических качеств (ПДК) механической части экипажа.

Известно, что исследование колебаний подвижного состава и его взаимодействия с рельсовым путем представляет собой задачу большой сложности, как на реальных конструкциях, так и при моделировании. При математическом моделировании свободные и вынужденные колебания экипажа описываются большим числом дифференциальных уравнений с нелинейными коэффициентами, что делает невозможным аналитическое решение этих уравнений без многочисленных и, зачастую, весьма грубых допущений, существенно снижающих научную и практическую ценность получаемых результатов.

Математическое моделирование на цифровых вычислительных машинах (ЭВМ) является одним из наиболее распространенных в настоящее время методов исследования колебаний. В основе его лежит созданиемодели, математическое описание колебательных процессов в которой подобно колебательным процессам, совершаемым реальным подвижным составом.

 

Анализ конструкции механической части выбранного для исследования экипажа. Выбор его параметров

Выбор характеристик масс, геометрических и инерционных характеристик выбранного экипажа

Массовые, инерционные и геометрические характеристики проектируемого подвижного состава принимаем равным соответствующим характеристикам существующего эпс, наиболее близкого по значению к проектируемому. Характеристики выбранного подвижного состава, близкого к проектируемому представлены в таблице 1.1.

Таблица 1.1 – Инерционные и геометрические характеристики проектируемого подвижного состава

Осевая формула	νК, км/ч	mK,т	mT,т	mKП,т	IУК, т·м^2	IУТ, т·м^2	2а2,м	2а1,м	Примечание
2о-2о		58,5	8,47			6,6		2,75	II-й класс тяговой передачи

Разработка кинематической схемы модели исследуемого экипажа и составление уравнений колебаний экипажа

Разработка кинематической схемы модели исследуемого экипажа

Для проведения необходимых исследований реальный экипаж заменяется кинематической схемой. При выборе расчётной кинематической схемы рекомендуется принять ряд общепринятых допущений:

1) Рассматриваются колебания только в продольной вертикальной плоскости, так как выполненные многочисленные теоретические и экспериментальные исследования показывают, что связь между колебаниями в продольно–вертикальной и продольно–поперечной плоскостях малая, поэтому эти колебания можно рассматривать как независимые.

2) Ввиду идентичности возмущений под левыми и правыми колёсами колёсной пары, расчётная схема может быть сведена к плоской.

3) Кузов, рамы тележек, колёсные пары и т.д. считаются абсолютно жёсткими телами, а их массы сосредоточены в центрах масс.

4) Упругие и диссипативные силы действуют по оси соответствующего упругого и диссипативного элемента.

5) В обоих ступенях подвешивания в качестве диссипативных элементов приняты элементы с жидкостным трением(гидравлические гасители колебаний).

Расчетная кинематическая схема экипажа представлена на рисунке 2.1.

Расчет парциальных частот колебаний

Используя выведенные уравнения, рассчитаем парциальные частоты колебаний:

 

Анализ результатов расчета

В данной работе будем исследовать вынужденные колебания с использование персонального компьютера. Для этого, в соответствии с 1 стр. 45 составим входной файл BXOD33.DAT в котором укажем основные параметры экипажа.

Расчет будем производить импортом в программу, написанную в оболочке Pascal, и далее производить следующие расчеты.

1. Построение амплитудно-частотных характеристик A _к1-η (f) и A_Fб1-η(f);

На основе полученных расчетов построим амплитудно-частотные характеристики A _к1-η (f) и A_Fб1-η(f) (Рисунок 3.1-3.2).

Рисунок 3.1 - Амплитудно-частотная характеристика ускорения первого шкворня кузова.

 

Рисунок 3.2 - Амплитудно-частотная характеристика сил в буксовом подвешивании.

При частоте 5,2 Гц амплитуда ускорения пола вагоне электропоезда над первым шкворнем достигает своего максимума как при скорости 50 км/ч, что близко к парциальной частоте подпрыгивания кузова следовательно возникает резонанс.

 

Максимальная амплитуда сил в первом буксовым подвешивании при скоростях 50 км/ч наблюдается при частоте 5,5 Гц, что близко к парциальной частоте подпрыгивания колёсной пары следовательно возникает резонанс.

 

2. Построение зависимостей показателей динамических качеств от скорости движения (Рисунок 3.3-3.6).

 

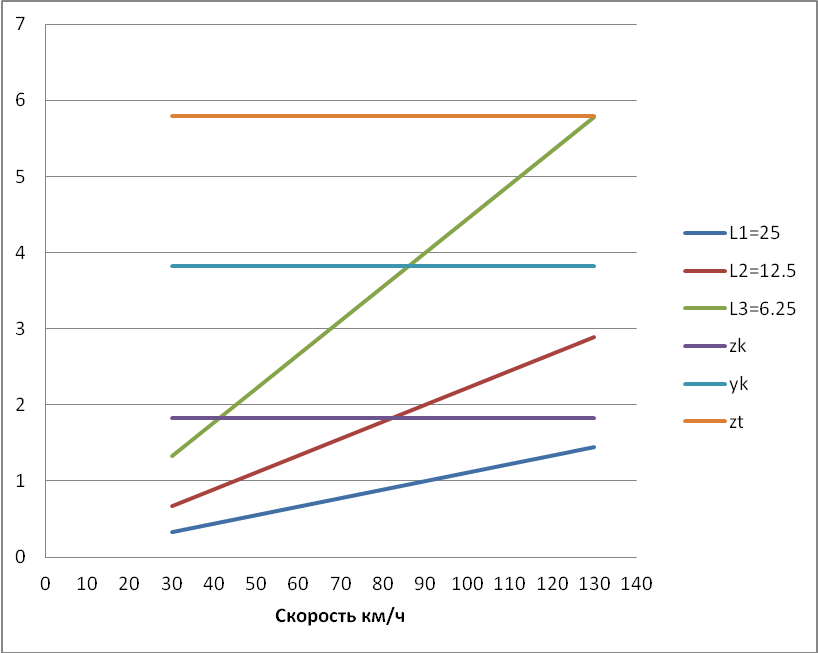
Рисунок 3.3 – График зависимости коэффициентов плавности хода от скорости.

 

 

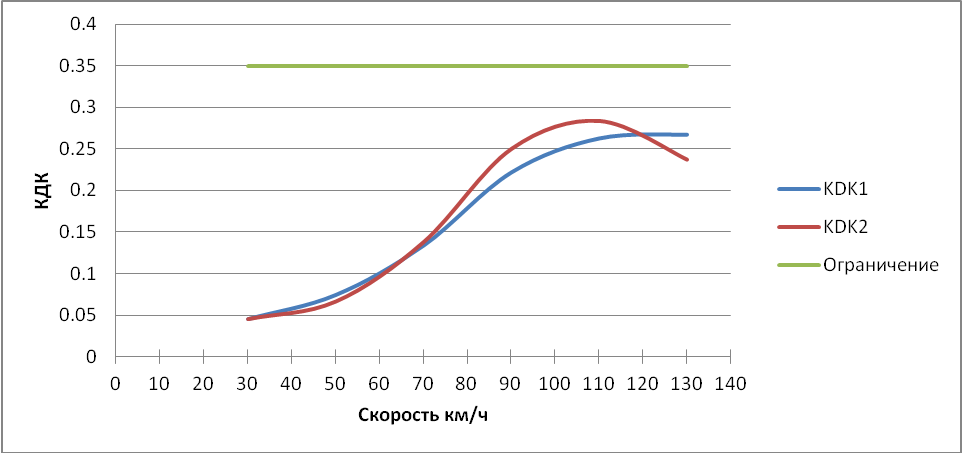
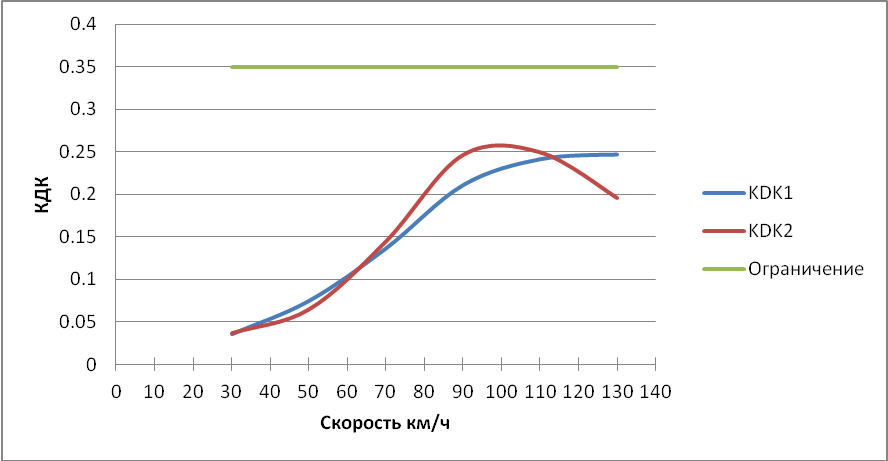
Рисунок 3.4 – График зависимости коэффициентов динамики кузова от скорости

 

 

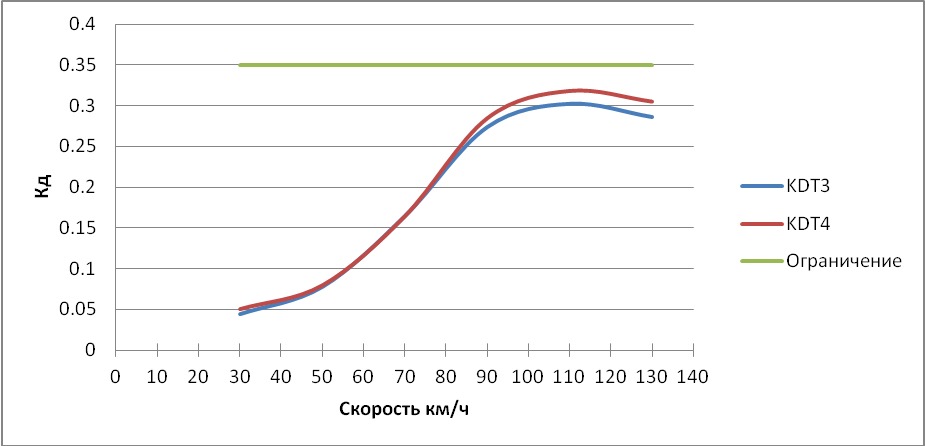
Рисунок 3.5 – График зависимости коэффициентов динамики тележки от скорости

 

Рисунок 3.6 – График зависимости коэффициентов динамики тележки от скорости

 

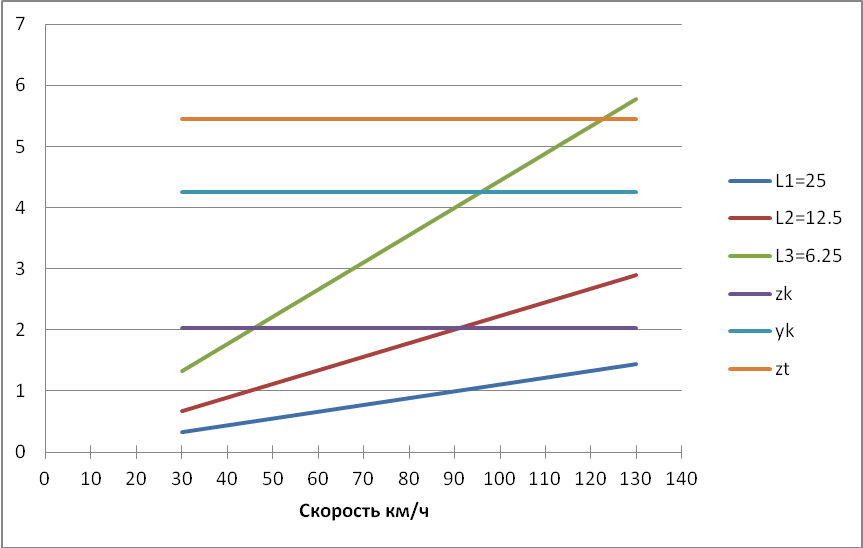
В процессе движения электровоза возможны резонансы, для выяснения этого построим диаграмму резонансных скоростей (Рисунок 3.6).

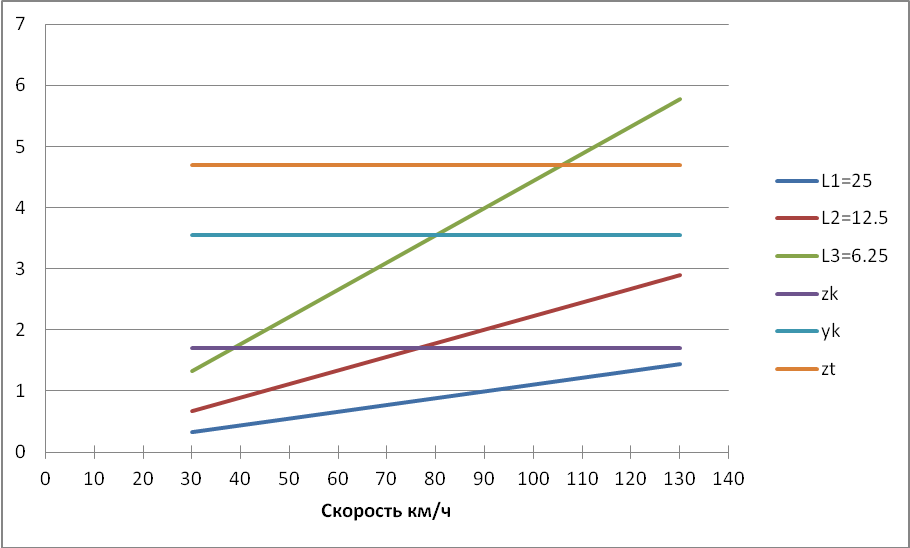
Рисунок 3.6 – Диаграмма резонансных скоростей

 

Как видно из графика плавности хода на скорости 80 км/ч и длины рельса 12,5 м метра возникает резонанс по подпрыгиванию кузова. Видимо колебания кузова на частоте 1,8 Гц увеличивают колебания надрессорного строения тележки. В связи с этим увеличим в 2 раза статический прогиб:

 

- для буксовой ступени рессорного подвешивания

- для кузовной ступени рессорного подвешивания

После этого произведем перерасчет жесткостей ступеней рессорного подвешивания.

а) определение жесткости кузовной ступени рессорного подвешивания.

Суммарная вертикальная жесткость кузовной ступени рессорного подвешивания, (1.2):

Вертикальная жесткость одного комплекта пружин кузовной ступени рессорного подвешивания равняется, (1.3):

б) определение жесткости буксовой ступени рессорного подвешивания

Суммарная вертикальная жесткость буксовой ступени рессорного подвешивания, (1.4):

Жесткость буксовой ступени рессорного подвешивания, приходящаяся на одну колесную пару, равняется, (1.5):

Рассчитываем диссипативные характеристики рессорного подвешивания

а) определение коэффициентов затухания гасителей колебаний для кузовной ступени рессорного подвешивания, (1.6):

Учитывая, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в кузовной ступени рессорного подвешивания показан гидравлический гаситель, его коэффициент затухания β _2z равен, (1.7):

б) определение коэффициентов затухания гасителей колебаний для буксовой ступени рессорного подвешивания, (1.8):

Учитывая также, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в буксовой ступени рессорного подвешивания стоит гидравлический гаситель, его коэффициент затухания β _1z равен, (1.9):

 

Рассчитаем парциальные частоты:

 

Парциальная частота подпрыгивания кузова:

 

Парциальная частота галопирования кузова:

Парциальная частота подпрыгивания тележки:

Парциальная частота галопирования тележки:

После изменений демпфировании в буксовом подвешивании построим новые графики и совместим с предыдущими. Для наглядности и правильных выводов (Рисунок 3.8-3.11).

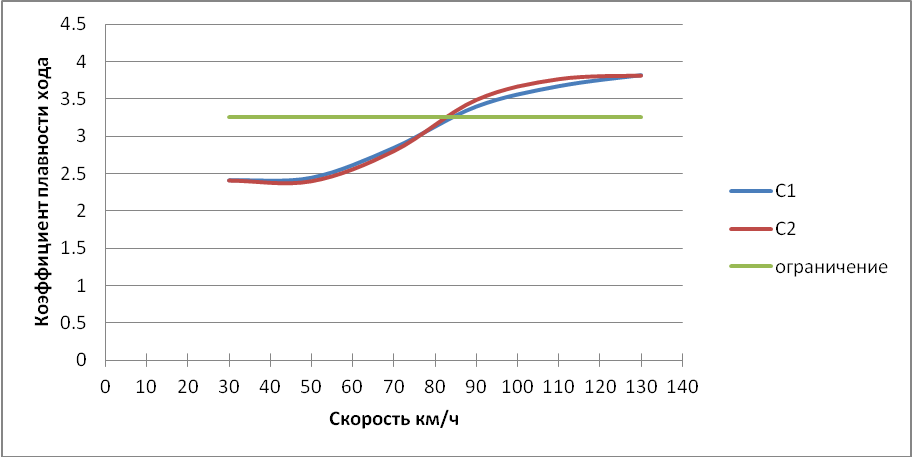
Рисунок 3.8 – Зависимость коэффициента плавности хода от скорости.

 

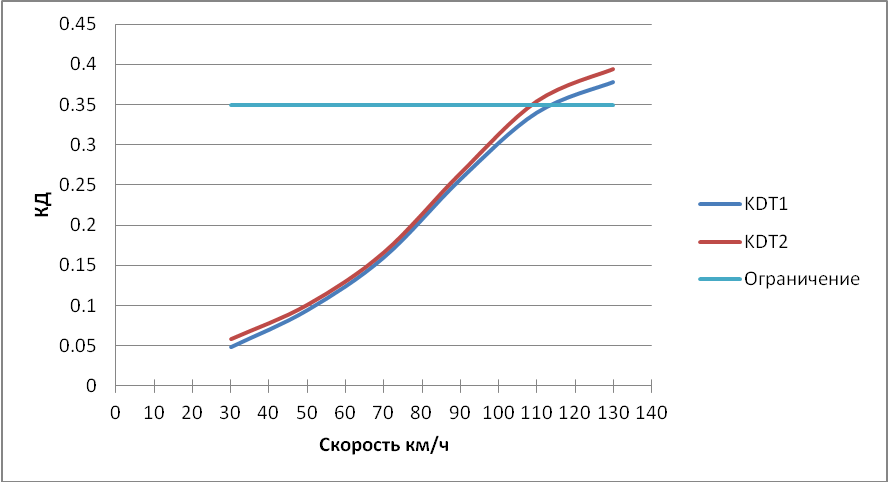
Рисунок 3.9 – Зависимость коэффициента динамики кузова от скорости.

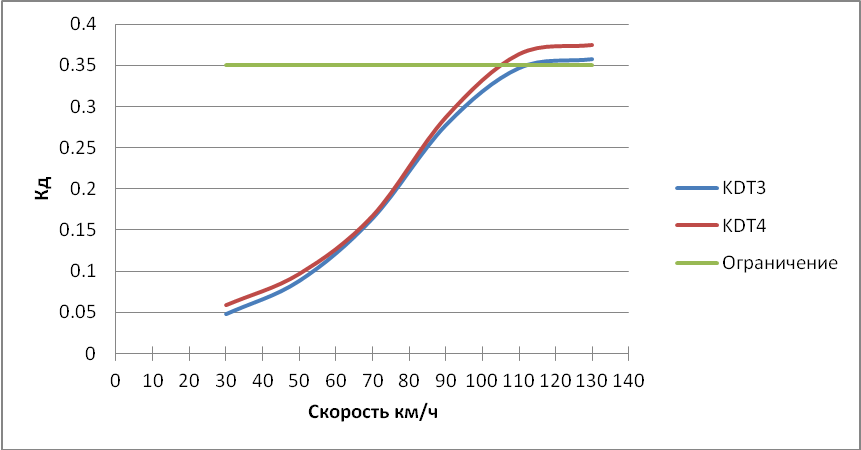
Рисунок 3.10 – Зависимость коэффициента динамики 1ой тележки от скорости.

Рисунок 3.11 – Зависимость коэффициента динамики 2ой тележки от скорости.

Рисунок 3.12 – Диаграмма резонансных скоростей

 

Как видно из графика плавности хода также на скорости 80 км/ч и длины рельса 12,5 м метра частота подпрыгивания кузова совпадает с частотой возмущения от рельса 12.5 м. Видимо колебания кузова на частоте 1,8 Гц увеличивают колебания надрессорного строения тележки. В связи с этим изменим еще раз статический прогиб:

- для буксовой ступени рессорного подвешивания

- для кузовной ступени рессорного подвешивания

После этого произведем перерасчет жесткостей ступеней рессорного подвешивания.

а) определение жесткости кузовной ступени рессорного подвешивания.

Суммарная вертикальная жесткость кузовной ступени рессорного подвешивания, (1.2):

Вертикальная жесткость одного комплекта пружин кузовной ступени рессорного подвешивания равняется, (1.3):

б) определение жесткости буксовой ступени рессорного подвешивания

Суммарная вертикальная жесткость буксовой ступени рессорного подвешивания, (1.4):

Жесткость буксовой ступени рессорного подвешивания, приходящаяся на одну колесную пару, равняется, (1.5):

Рассчитываем диссипативные характеристики рессорного подвешивания

а) определение коэффициентов затухания гасителей колебаний для кузовной ступени рессорного подвешивания, (1.6):

Учитывая, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в кузовной ступени рессорного подвешивания показан гидравлический гаситель, его коэффициент затухания β _2z равен, (1.7):

б) определение коэффициентов затухания гасителей колебаний для буксовой ступени рессорного подвешивания, (1.8):

Учитывая также, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в буксовой ступени рессорного подвешивания стоит гидравлический гаситель, его коэффициент затухания β _1z равен, (1.9):

 

Расчитаем парциальные частоты:

 

Парциальная частота подпрыгивания кузова:

 

Парциальная частота галопирования кузова:

 

Парциальная частота подпрыгивания тележки:

Парциальная частота галопирования тележки:

 

После изменений демпфировании в буксовом подвешивании построим новые графики и совместим с предыдущими для наглядности и правильных выводов (Рисунок 3.13-3.16).

Рисунок 3.13 – Зависимость коэффициента плавности хода от скорости.

 

Рисунок 3.14 – Зависимость коэффициента динамики кузова от скорости.

Рисунок 3.15 – Зависимость коэффициента динамики 1ой тележки от скорости.

Рисунок 3.16 – Зависимость коэффициента динамики 2ой тележки от скорости.

Рисунок 3.17 – Диаграмма резонансных скоростей

 

 

Вывод: в результате изменения статического прогиба мы добились поставленной цели, так как коэффициенты динамики тележки и коэффициент динамики кузова находятся в пределах нормы, а коэффициент плавности хода выходит за её пределы на скорости 80 км/ч. Следовательно, чтобы изменить, необходимо поменять коэффициенты демпфирования.

		3336,5	54,6	110,4	0,35	0,25
	3674,8	3877,6	76,3	168,3	0,35	0,25
	2572,4	4782,4	50,7	187,005	0,35	0,25

Рисунок 3.12 – Зависимость утроенного среднеквадратического значения перемещения первого и второго шкворня от скорости

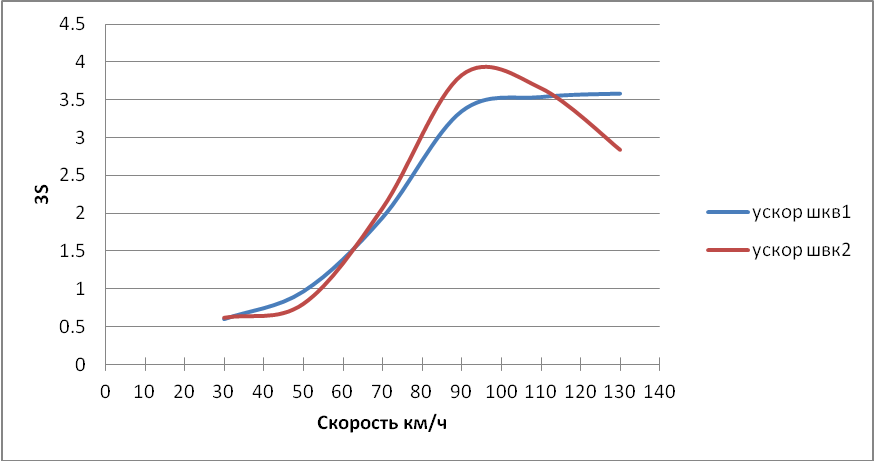
Рисунок 3.13 – Зависимость утроенного среднеквадратического значения ускорения первого и второго шкворня от скорости

Рисунок 3.14 – Зависимость утроенного среднеквадратического значения сил в центральных подвешиваниях от скорости

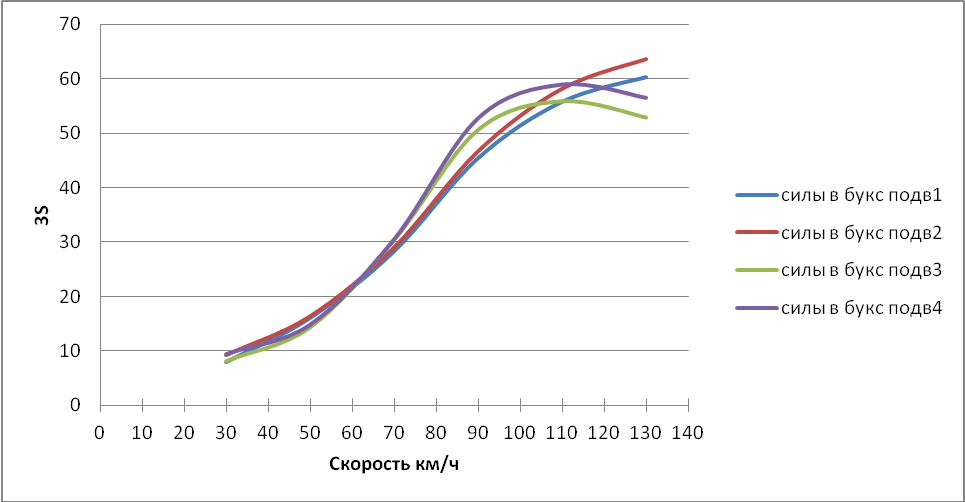
Рисунок 3.15 – Зависимость утроенного среднеквадратического значения сил в буксовых подвешиваниях от скорости

 

ЗАКЛЮЧЕНИЕ

В курсовой работе разработал механо - математическую модель заданного экипажа, составили дифференциальные уравнения его колебаний и рассчитали показатель его динамических качеств.

На основании полученных данных выполнил оценку неравенства V_K£[V] т.е. допустимая скорость движения не должна превышать конструкционную скорость. Заданная конструкционная скорость 130 км/ч, а по показателям коэффициента плавности хода тележки получил допустимую скорость равную 80 км/ч. Сравнивая эти скорости выяснил, что [V] £V_K и данный экипаж эксплуатировать можно со скоростью не более 80 км/ч, а также не рекомендуется длительное движение с резонансной скоростью 100 км/ч.

 

 

Введение

Необходимость повышения скорости движения подвижного состава по рельсовому пути при безусловном обеспечении безопасности в условиях нарастания уровня совместных колебаний пути подвижного состава предъявляет высокие требования к совершенствованию механической части электроподвижного состава (э.п.с.) с точки зрения улучшения его динамических качеств.

В этих условиях исследование колебаний должно являться определяющим при выборе параметров механической части э.п.с. При этом задача исследования заключается в выборе такой системы и параметров рессорного подвешивания, которые обеспечивали бы:

· наилучшие динамические качества экипажа;

· устойчивость движения экипажа в рельсовой колее при выполнении требований к показателям безопасности движения;

· выполнения требований к показателям динамических качеств (ПДК) механической части экипажа.

Известно, что исследование колебаний подвижного состава и его взаимодействия с рельсовым путем представляет собой задачу большой сложности, как на реальных конструкциях, так и при моделировании. При математическом моделировании свободные и вынужденные колебания экипажа описываются большим числом дифференциальных уравнений с нелинейными коэффициентами, что делает невозможным аналитическое решение этих уравнений без многочисленных и, зачастую, весьма грубых допущений, существенно снижающих научную и практическую ценность получаемых результатов.

Математическое моделирование на цифровых вычислительных машинах (ЭВМ) является одним из наиболее распространенных в настоящее время методов исследования колебаний. В основе его лежит созданиемодели, математическое описание колебательных процессов в которой подобно колебательным процессам, совершаемым реальным подвижным составом.

 

Анализ конструкции механической части выбранного для исследования экипажа. Выбор его параметров