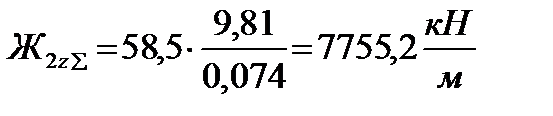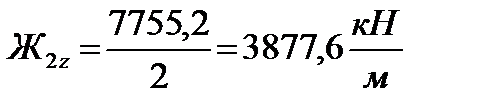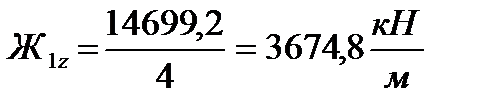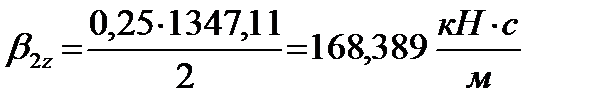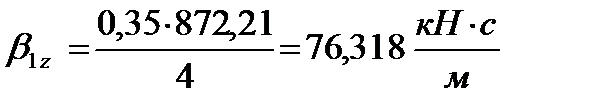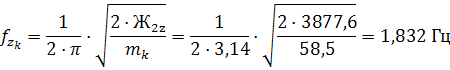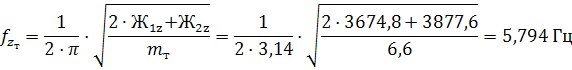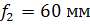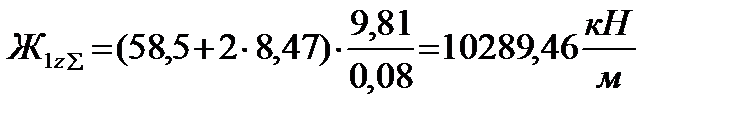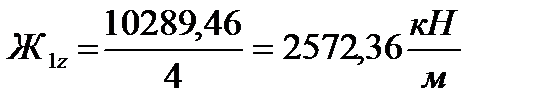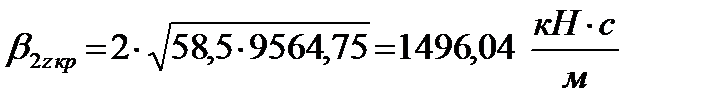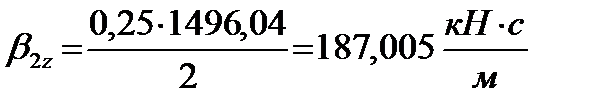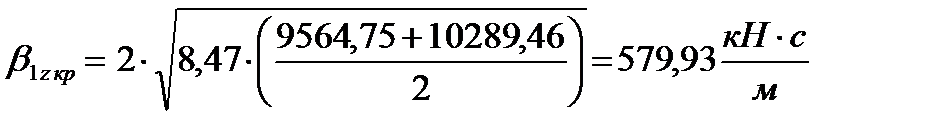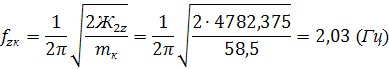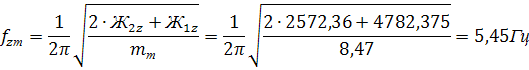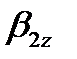Анализ методов исследования вынужденных колебаний выбранного экипажа

Известны три основных метода исследования колебаний подвижного состава:

– с помощью натурного эксперимента на реальных конструкциях подвижного состава;

– на физических моделях подвижного состава;

– методом математического моделирования с применением современной

вычислительной техники путём замены реального экипажа и пути их

математической моделью.

В последнее двадцать лет вычислительная техника очень активно

развивается: увеличивается ее быстродействие и объем оперативной памяти.

Современные персональные компьютеры позволяют создавать математические модели сложных динамических систем экипаж-путь, которые с большой достоверностью описывают колебательные процессы, происходящие на реальном подвижном составе. Учитывая это, методы математического моделирования, ввиду их дешевизны, получили большое распространение для оценки ходовых качеств на этапе проектирования новых образцов подвижного состава или модернизации существующих. В ходе многочисленных исследований на ЭВМ и различных методах моделирования, получили следующее.

При движении со скоростями, близкими к скоростям, соответствующим высокочастотному резонансу, подрессоренная масса остается практически неподвижной, а колеса совершают колебания, поэтому колебания груза почти не влияют на нагрузки в ходовой части, а решающее влияние оказывают колебания неподрессоренных масс.

Под длинными и короткими неровностями следует понимать такие неровности, продолжительность воздействия возмущающих функций от воздействия которых близка соответственно к периоду собственных колебаний подрессоренной массы и к периоду колебаний неподрессоренных масс подвижного состава.

При исследовании нагрузок на ходовую часть от колебаний подрессоренной и неподрессоренных масс целесообразно рассматривать эквивалентные схемы динамических систем для случаев движения по коротким и длинным неровностям. При колебаниях в области низких собственных частот, которые вызывают значительные вертикальные и угловые перемещения подрессоренной массы и соответственно большие перегрузки в ходовой части (при достаточной разнице низких и высоких собственных частот), можно пренебречь влиянием неподрессоренных масс.

 

Показатели динамических качеств

Понятие «качество» охватывает свойства объекта, которые обусловливают его пригодность удовлетворять определенным требованиям в соответствии с назначением объектов. Количественную характеристику такой пригодности объектов описывают с помощью показателей качества, выбор которых зависит от назначения объекта.

Для объектов многоцелевого назначения, таких, например, как ЭПС, может быть значительное количество показателей как безразмерных, так и выражаемых в различных единицах, например в километрах в час, часах и т. п.

Показатели качества подразделяются на 11 основных групп: назначения; безопасности; экономичного использования сырья, материалов, топлива, энергии; надежности; эргономические; эстетические; технологические; транспортабельности; стандартизации и унификации; патентно-правовые; экологические.

Каждая из этих групп в свою очередь делится на подгруппы: например, показатели назначения – классификационные, функциональные и технической эффективности, конструктивные, состава и структуры; показатели безопасности – физические, химические, биологические, психофизиологические; показатели надежности – безотказности, долговечности, ремонтопригодности, сохраняемости; показатели эргономические – гигиенические, антропометрические, физиологические, психофизиологические, психологические.

Применительно к механической части показатели качества делят на два больших класса:

· первый – общие для механической части и локомотива в целом как единого технического средства;

· второй – специфические для механической части, учитывающие ее основные особенности, отличающие механическую часть от других составных частей локомотива.

К специфическим относят показатели, которые характеризуют поведение локомотива как механической системы при движении по рельсовому пути. Поскольку определяющую роль при этом играют колебательные процессы, эти показатели принято называть показателями динамических качеств (ПДК). К ним относят показатели:

1) виброзащиты, определяющие степень защиты оборудования локомотива, а также пути от вибраций, возникающих при движении локомотива;

2) безопасности движения, характеризующие степень обеспечения безаварийности движения по рельсовой колее;

3) плавности хода, относящиеся к подгруппе гигиенических показателей и характеризующие степень воздействия вибраций локомотива на организм человека.

Проектирование, изготовление, эксплуатация и ремонт подвижного состава выполняются таким образом, чтобы обеспечивался допустимый уровень ПДК в течение всего срока его службы.

Из всех общих показателей качества локомотивов ограничимся рассмотрением основных групп: показателей назначения и безопасности.

Анализ результатов расчета

В данной работе будем исследовать вынужденные колебания с использование персонального компьютера. Для этого, в соответствии с 1 стр. 45 составим входной файл BXOD33.DAT в котором укажем основные параметры экипажа.

Расчет будем производить импортом в программу, написанную в оболочке Pascal, и далее производить следующие расчеты.

1. Построение амплитудно-частотных характеристик A _к1-η (f) и A_Fб1-η(f);

На основе полученных расчетов построим амплитудно-частотные характеристики A _к1-η (f) и A_Fб1-η(f) (Рисунок 3.1-3.2).

Рисунок 3.1 - Амплитудно-частотная характеристика ускорения первого шкворня кузова.

 

Рисунок 3.2 - Амплитудно-частотная характеристика сил в буксовом подвешивании.

При частоте 5,2 Гц амплитуда ускорения пола вагоне электропоезда над первым шкворнем достигает своего максимума как при скорости 50 км/ч, что близко к парциальной частоте подпрыгивания кузова следовательно возникает резонанс.

 

Максимальная амплитуда сил в первом буксовым подвешивании при скоростях 50 км/ч наблюдается при частоте 5,5 Гц, что близко к парциальной частоте подпрыгивания колёсной пары следовательно возникает резонанс.

 

2. Построение зависимостей показателей динамических качеств от скорости движения (Рисунок 3.3-3.6).

 

Рисунок 3.3 – График зависимости коэффициентов плавности хода от скорости.

 

 

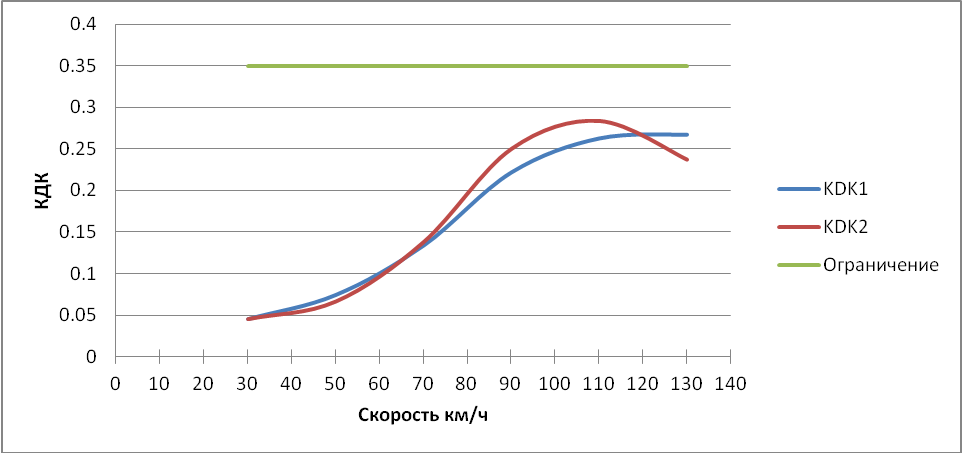
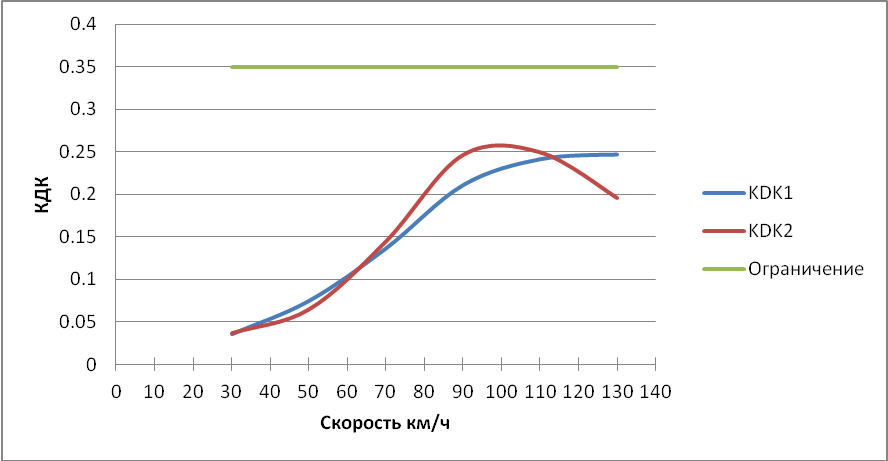
Рисунок 3.4 – График зависимости коэффициентов динамики кузова от скорости

 

 

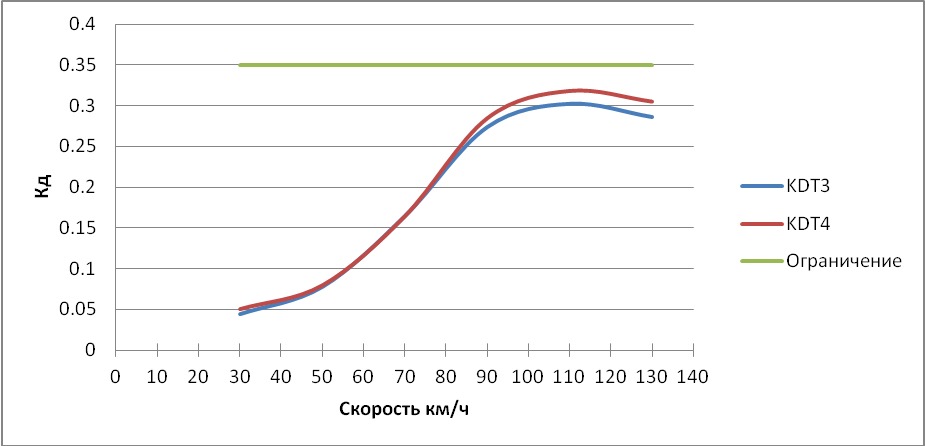
Рисунок 3.5 – График зависимости коэффициентов динамики тележки от скорости

 

Рисунок 3.6 – График зависимости коэффициентов динамики тележки от скорости

 

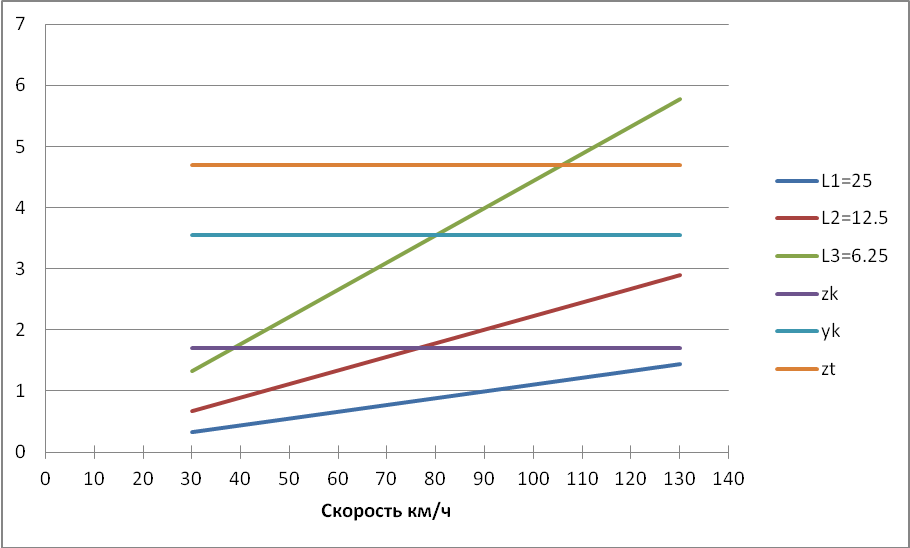
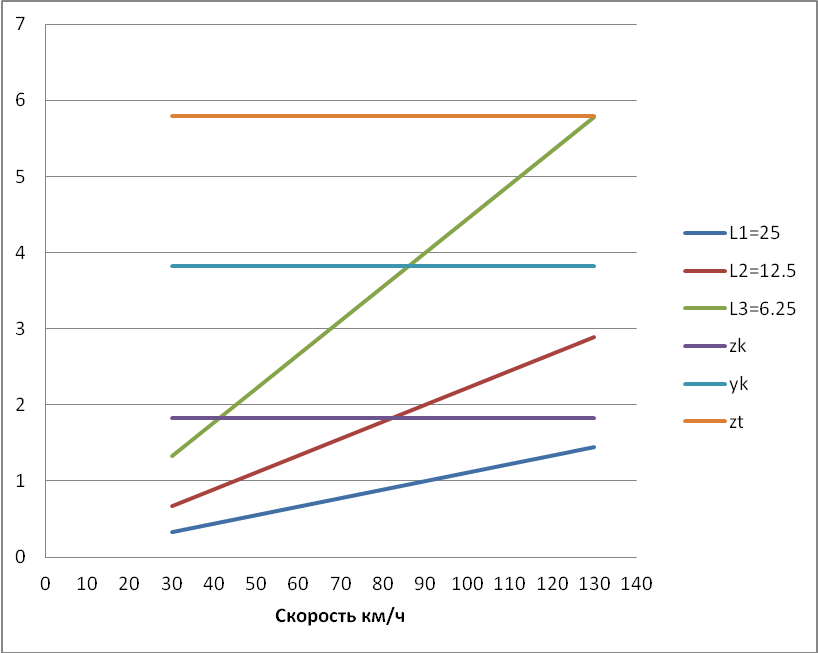
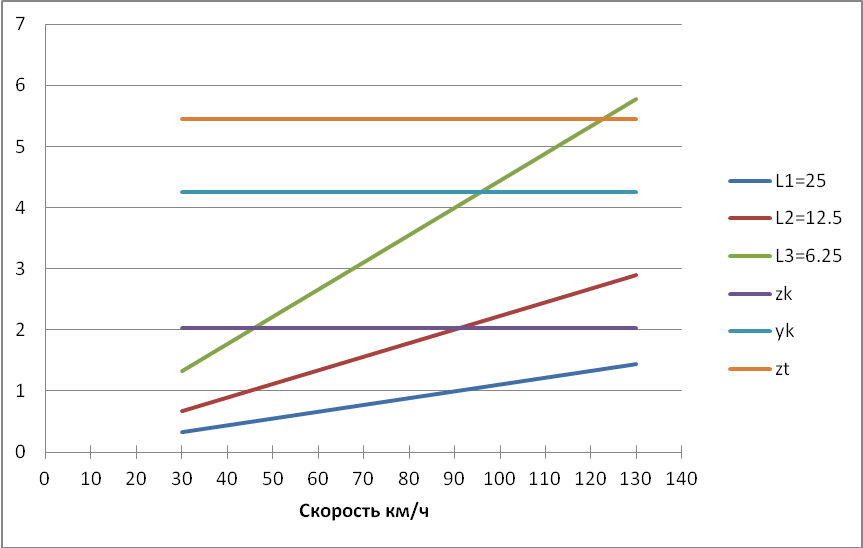
В процессе движения электровоза возможны резонансы, для выяснения этого построим диаграмму резонансных скоростей (Рисунок 3.6).

Рисунок 3.6 – Диаграмма резонансных скоростей

 

Как видно из графика плавности хода на скорости 80 км/ч и длины рельса 12,5 м метра возникает резонанс по подпрыгиванию кузова. Видимо колебания кузова на частоте 1,8 Гц увеличивают колебания надрессорного строения тележки. В связи с этим увеличим в 2 раза статический прогиб:

 

- для буксовой ступени рессорного подвешивания

- для кузовной ступени рессорного подвешивания

После этого произведем перерасчет жесткостей ступеней рессорного подвешивания.

а) определение жесткости кузовной ступени рессорного подвешивания.

Суммарная вертикальная жесткость кузовной ступени рессорного подвешивания, (1.2):

Вертикальная жесткость одного комплекта пружин кузовной ступени рессорного подвешивания равняется, (1.3):

б) определение жесткости буксовой ступени рессорного подвешивания

Суммарная вертикальная жесткость буксовой ступени рессорного подвешивания, (1.4):

Жесткость буксовой ступени рессорного подвешивания, приходящаяся на одну колесную пару, равняется, (1.5):

Рассчитываем диссипативные характеристики рессорного подвешивания

а) определение коэффициентов затухания гасителей колебаний для кузовной ступени рессорного подвешивания, (1.6):

Учитывая, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в кузовной ступени рессорного подвешивания показан гидравлический гаситель, его коэффициент затухания β _2z равен, (1.7):

б) определение коэффициентов затухания гасителей колебаний для буксовой ступени рессорного подвешивания, (1.8):

Учитывая также, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в буксовой ступени рессорного подвешивания стоит гидравлический гаситель, его коэффициент затухания β _1z равен, (1.9):

 

Рассчитаем парциальные частоты:

 

Парциальная частота подпрыгивания кузова:

 

Парциальная частота галопирования кузова:

Парциальная частота подпрыгивания тележки:

Парциальная частота галопирования тележки:

После изменений демпфировании в буксовом подвешивании построим новые графики и совместим с предыдущими. Для наглядности и правильных выводов (Рисунок 3.8-3.11).

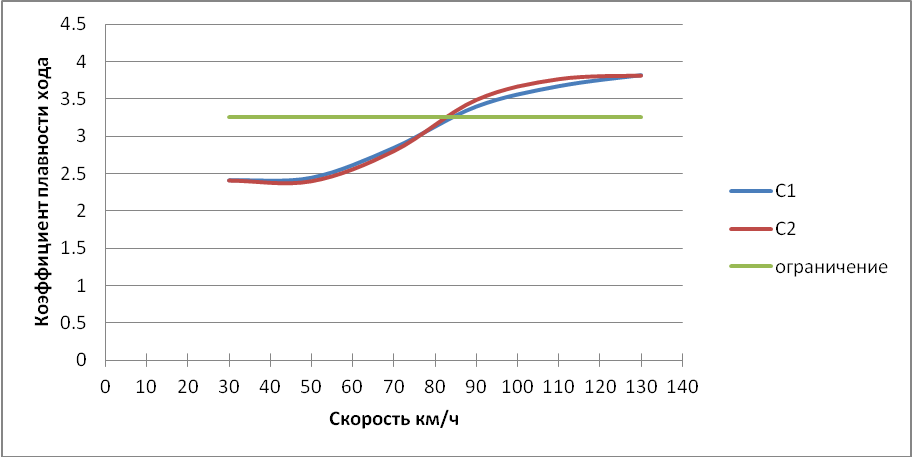
Рисунок 3.8 – Зависимость коэффициента плавности хода от скорости.

 

Рисунок 3.9 – Зависимость коэффициента динамики кузова от скорости.

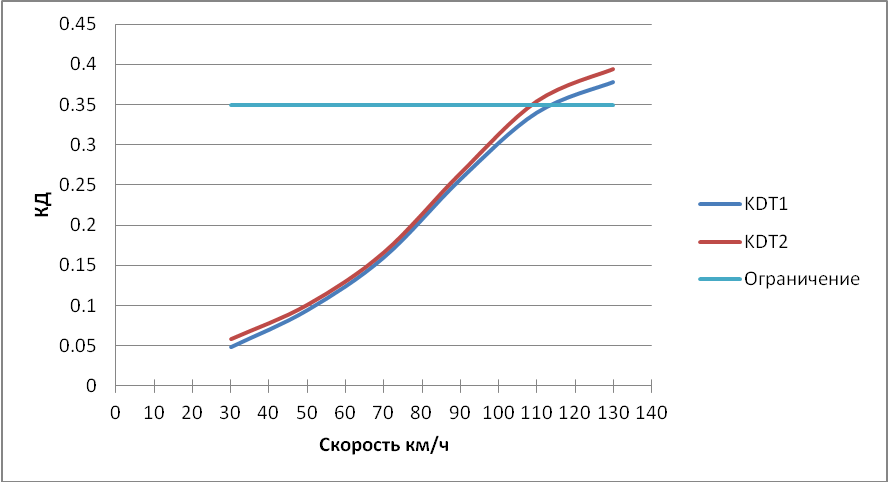
Рисунок 3.10 – Зависимость коэффициента динамики 1ой тележки от скорости.

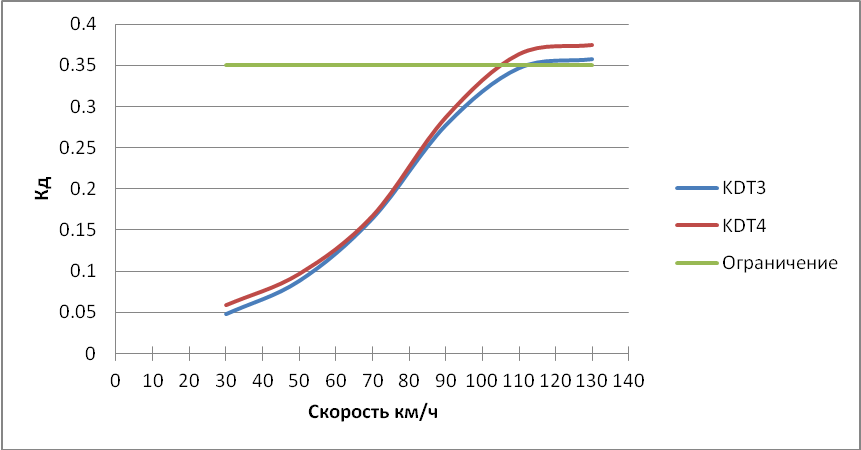
Рисунок 3.11 – Зависимость коэффициента динамики 2ой тележки от скорости.

Рисунок 3.12 – Диаграмма резонансных скоростей

 

Как видно из графика плавности хода также на скорости 80 км/ч и длины рельса 12,5 м метра частота подпрыгивания кузова совпадает с частотой возмущения от рельса 12.5 м. Видимо колебания кузова на частоте 1,8 Гц увеличивают колебания надрессорного строения тележки. В связи с этим изменим еще раз статический прогиб:

- для буксовой ступени рессорного подвешивания

- для кузовной ступени рессорного подвешивания

После этого произведем перерасчет жесткостей ступеней рессорного подвешивания.

а) определение жесткости кузовной ступени рессорного подвешивания.

Суммарная вертикальная жесткость кузовной ступени рессорного подвешивания, (1.2):

Вертикальная жесткость одного комплекта пружин кузовной ступени рессорного подвешивания равняется, (1.3):

б) определение жесткости буксовой ступени рессорного подвешивания

Суммарная вертикальная жесткость буксовой ступени рессорного подвешивания, (1.4):

Жесткость буксовой ступени рессорного подвешивания, приходящаяся на одну колесную пару, равняется, (1.5):

Рассчитываем диссипативные характеристики рессорного подвешивания

а) определение коэффициентов затухания гасителей колебаний для кузовной ступени рессорного подвешивания, (1.6):

Учитывая, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в кузовной ступени рессорного подвешивания показан гидравлический гаситель, его коэффициент затухания β _2z равен, (1.7):

б) определение коэффициентов затухания гасителей колебаний для буксовой ступени рессорного подвешивания, (1.8):

Учитывая также, что на расчетной кинематической схеме параллельно каждой вертикальной пружине в буксовой ступени рессорного подвешивания стоит гидравлический гаситель, его коэффициент затухания β _1z равен, (1.9):

 

Расчитаем парциальные частоты:

 

Парциальная частота подпрыгивания кузова:

 

Парциальная частота галопирования кузова:

 

Парциальная частота подпрыгивания тележки:

Парциальная частота галопирования тележки:

 

После изменений демпфировании в буксовом подвешивании построим новые графики и совместим с предыдущими для наглядности и правильных выводов (Рисунок 3.13-3.16).

Рисунок 3.13 – Зависимость коэффициента плавности хода от скорости.

 

Рисунок 3.14 – Зависимость коэффициента динамики кузова от скорости.

Рисунок 3.15 – Зависимость коэффициента динамики 1ой тележки от скорости.

Рисунок 3.16 – Зависимость коэффициента динамики 2ой тележки от скорости.

Рисунок 3.17 – Диаграмма резонансных скоростей

 

 

Вывод: в результате изменения статического прогиба мы добились поставленной цели, так как коэффициенты динамики тележки и коэффициент динамики кузова находятся в пределах нормы, а коэффициент плавности хода выходит за её пределы на скорости 80 км/ч. Следовательно, чтобы изменить, необходимо поменять коэффициенты демпфирования.

		3336,5	54,6	110,4	0,35	0,25
	3674,8	3877,6	76,3	168,3	0,35	0,25
	2572,4	4782,4	50,7	187,005	0,35	0,25

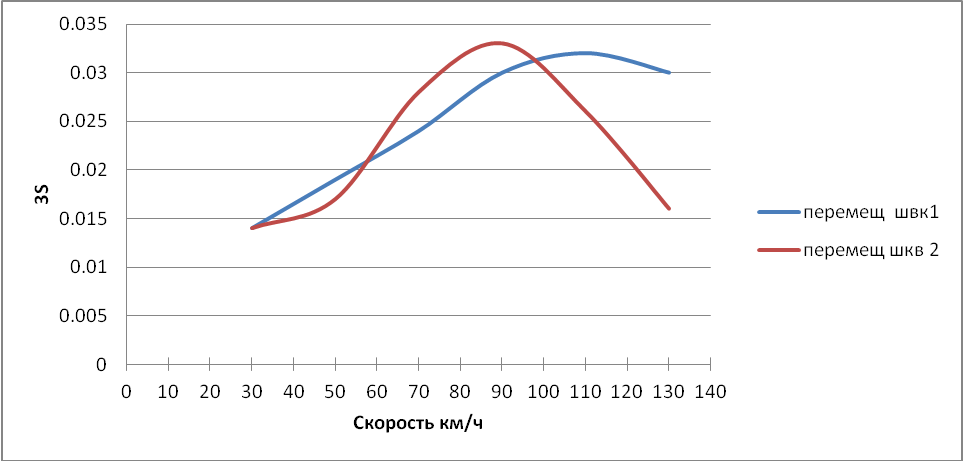
Рисунок 3.12 – Зависимость утроенного среднеквадратического значения перемещения первого и второго шкворня от скорости

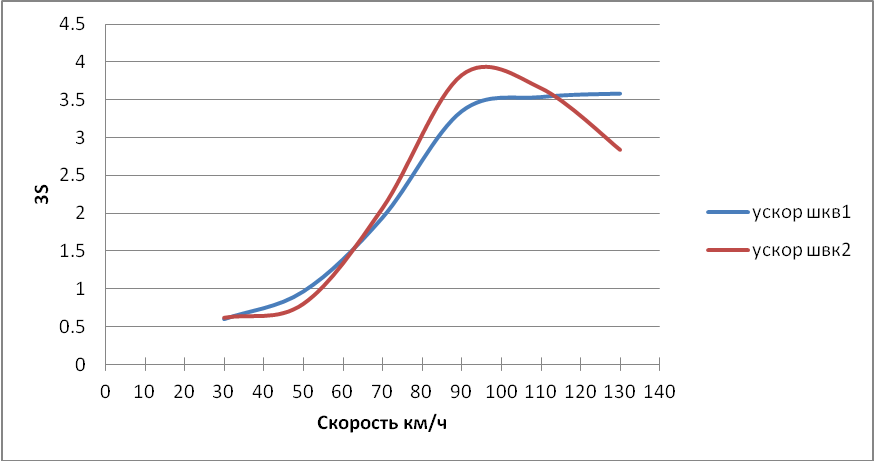
Рисунок 3.13 – Зависимость утроенного среднеквадратического значения ускорения первого и второго шкворня от скорости

Рисунок 3.14 – Зависимость утроенного среднеквадратического значения сил в центральных подвешиваниях от скорости

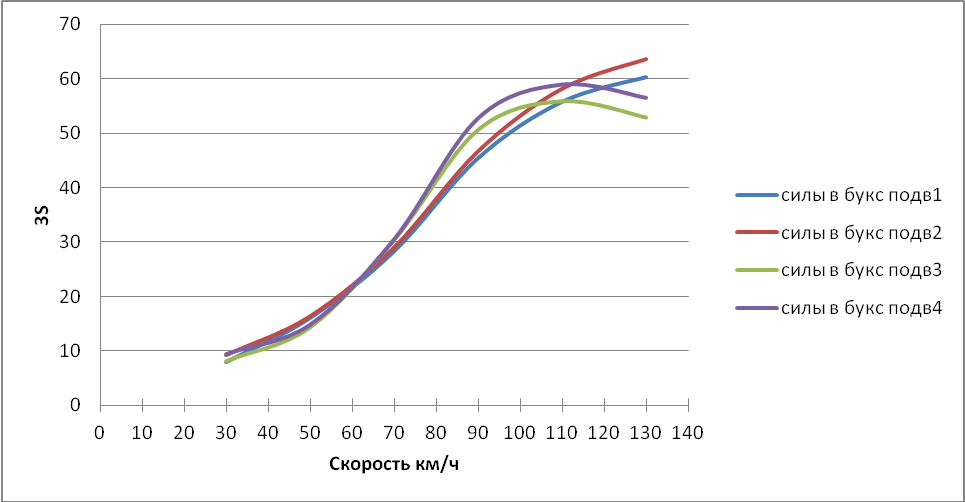
Рисунок 3.15 – Зависимость утроенного среднеквадратического значения сил в буксовых подвешиваниях от скорости

 

ЗАКЛЮЧЕНИЕ

В курсовой работе разработал механо - математическую модель заданного экипажа, составили дифференциальные уравнения его колебаний и рассчитали показатель его динамических качеств.

На основании полученных данных выполнил оценку неравенства V_K£[V] т.е. допустимая скорость движения не должна превышать конструкционную скорость. Заданная конструкционная скорость 130 км/ч, а по показателям коэффициента плавности хода тележки получил допустимую скорость равную 80 км/ч. Сравнивая эти скорости выяснил, что [V] £V_K и данный экипаж эксплуатировать можно со скоростью не более 80 км/ч, а также не рекомендуется длительное движение с резонансной скоростью 100 км/ч.