
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента динамической вязкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предположим, что газ течет неперемешивающимися слоями. Опыт показывает, что если скорость V движения газа меняется от слоя к слою, то между двумя смежными слоями действует сила внутреннего трения F:
где Молекулярно–кинетическая теория устанавливает следующее выражение для коэффициента динамической вязкости идеальных газов:
На практике эта зависимость выполняется с точностью до коэффициента. Более точной является формула:
Здесь, как и в предыдущей формуле, h – коэффициент внутреннего трения газа, r – плотность газа,
Для ламинарного течения несжимаемого газа через цилиндрическую трубу длины l и диаметра d справедлива формула Пуазейля:
где D V – объем газа, протекающий за время D t через эту трубу, D p – разность давлений на концах трубы, h – коэффициент вязкости газа. Для бесконечно малого промежутка времени dt формулу (5) можно переписать в виде:
Формула (6) является основой для определения коэффициента динамической вязкости. Экспериментальная установка (рис. 15) состоит из двух сообщающихся сосудов: длинной стеклянной трубки А, закрытой пробкой П с капилляром, и широкого сосуда В, который можно перемещать по стойке С установки в вертикальном направлении. Сосуд В снабжен пробкой с трехходовым краном К, который посредством резиновой трубки соединен с ручным насосом. Существует три положения крана: а) сосуд В соединен с насосом (
Рис. 15
Рассмотрим течение газа через капилляр под действием разностей уровней жидкости в широком и узком сосуде (рис. 15). При этом разность давлений на входе и выходе капилляра невелика, поэтому можно пользоваться формулой (6). Если широкий сосуд сообщен с атмосферой, то через капилляр просачивается воздух, так как разность уровней жидкости создает на концах капилляра разность давлений:
где r – плотность жидкости, g – ускорение свободного падения, h – разность уровней жидкости в сосудах. Пусть V – объем воздуха в узком сосуде. Очевидно, что
где S – сечение сосуда, t – время. Знак (–) указывает, что объем газа растет, а высота жидкости уменьшается. Подставляя (7) и (8) в (6) и вводя обозначение
после простых преобразований получим:
Это – дифференциальное уравнение экспоненциально затухающего процесса. Если при t 0 = 0 h = h 0, тогда решение его имеет вид:
Измерив через равные промежутки времени высоту столба жидкости в трубе, можно по этим данным построить график линейной зависимости между
Определение длины свободного пробега молекул Для определения средней длины свободного пробега молекул можно воспользоваться соотношением (4). При этом плотность воздуха в тех условиях, в которых определяется коэффициент вязкости, можно найти из уравнения Клапейрона–Менделеева:
где p – атмосферное давление, m – молярная масса воздуха, R – универсальная газовая постоянная, Т – температура воздуха. Среднеарифметическая скорость воздуха вычисляется по формуле:
Объединяя (4), (13), (14), получаем:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.96 (0.006 с.) |

 , (1)
, (1) – градиент скорости, т.е. величина, показывающая, как быстро меняется скорость движения газа V в направлении, перпендикулярном к поверхности, разделяющей слои, S – величина поверхности, вдоль которой действует сила, h – коэффициент пропорциональности, называемый коэффициентом внутреннего трения или коэффициентом динамической вязкости. В системе СГС он измеряется в пуазах (Пз): 1 Пз = 1 г/ (см×с), а в системе СИ – в Па×с или в кг/(м×с).
– градиент скорости, т.е. величина, показывающая, как быстро меняется скорость движения газа V в направлении, перпендикулярном к поверхности, разделяющей слои, S – величина поверхности, вдоль которой действует сила, h – коэффициент пропорциональности, называемый коэффициентом внутреннего трения или коэффициентом динамической вязкости. В системе СГС он измеряется в пуазах (Пз): 1 Пз = 1 г/ (см×с), а в системе СИ – в Па×с или в кг/(м×с).
 . (2)
. (2) . (3)
. (3) – средняя длина свободного пробега молекул газа,
– средняя длина свободного пробега молекул газа,  – средняя арифметическая скорость молекул, k – коэффициент пропорциональности, который зависит от числа степеней свободы газа и учитывает распределение по скоростям. Для воздуха k = 0.5, соотношение (3) имеет вид:
– средняя арифметическая скорость молекул, k – коэффициент пропорциональности, который зависит от числа степеней свободы газа и учитывает распределение по скоростям. Для воздуха k = 0.5, соотношение (3) имеет вид: . (4)
. (4) , (5)
, (5) . (6)
. (6) ); б) сосуд соединен с атмосферой и отключен от насоса (
); б) сосуд соединен с атмосферой и отключен от насоса ( ); в) сосуд соединен с атмосферой и насосом (
); в) сосуд соединен с атмосферой и насосом ( ). Положения а) и б) являются рабочими. Имеется также шкала, по которой можно отмечать положение жидкости в узком сосуде и поддерживать ее в широком сосуде на одном уровне.
). Положения а) и б) являются рабочими. Имеется также шкала, по которой можно отмечать положение жидкости в узком сосуде и поддерживать ее в широком сосуде на одном уровне.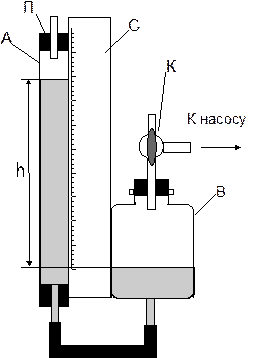
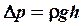 , (7)
, (7) , (8)
, (8) , (9)
, (9) . (10)
. (10) . (11)
. (11) и t. По графику легко найти коэффициент b, а зная b, по формуле (9). можно вычислить коэффициент динамической вязкости газа h:
и t. По графику легко найти коэффициент b, а зная b, по формуле (9). можно вычислить коэффициент динамической вязкости газа h: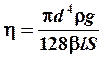 . (12)
. (12)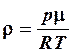 , (13)
, (13)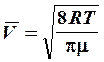 . (14)
. (14)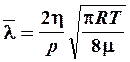 . (15)
. (15)


