
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение эффективного диаметра молекулСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для этого обратимся к выражению
где s – эффективный диаметр молекул, n – концентрация молекул газа. Концентрация молекул воздуха при данной температуре может быть найдена следующим образом:
где p 0, Т 0 и p, Т – давление и температура воздуха при нормальных условиях и в условиях опыта соответственно, n 0 – концентрация молекул воздуха при нормальных условиях (число Лошмидта). Расчетная формула для эффективного диаметра молекул воздуха имеет, таким образом, вид:
ИЗМЕРЕНИЯ И ОБРАБОТКА ИХ РЕЗУЛЬТАТОВ
Определение коэффициента динамической вязкости 1. С помощью насоса поднимите уровень жидкости в трубке до некоторого значения h > h 0 (h 0 задается преподавателем). Внимание! Подъем воды в жидкости осуществлять мелкими качками, во избежание ее выливания. 2. Установите уровень жидкости в широком сосуде на нуле. 3. Соедините широкий сосуд с атмосферой и, когда высота жидкости в узком сосуде станет равна h 0, включите секундомер. Поддерживая уровень жидкости в широком сосуде около нуля, замерьте время опускания жидкости до высоты на 5 см ниже h 0. Проделайте это измерение не менее трех раз и вычислите среднее значение t. 4. Аналогичным образом замерьте время опускания жидкости на 10 см, 15 см, и т.д. ниже h 0. Всего должно быть измерено время опускания столба жидкости до не менее чем 7-8 отметок. 5. Для каждого измерения вычислите Таблица 11
6. По данным таблицы постройте график функции 7. По графику найдите численное значение углового коэффициента и по формуле (12) – коэффициент вязкости воздуха. Параметры установки, входящие в рабочую формулу обозначены на установке.
Определение длины свободного пробега молекул Зная коэффициент вязкости воздуха h и измерив атмосферное давление барометром, а температуру – термометром, по формуле (15) вычислите среднюю длину свободного пробега молекул воздуха в системе СИ. Молярная масса воздуха m = 28.95 кг/кмоль, R = 8.31 Дж /(моль×К).
Определение эффективного диаметра молекул По формуле (18) рассчитайте, воспользовавшись предыдущими результатами, эффективный диаметр молекул воздуха. При этом: p 0 = 101325 Па, n 0 = 2,69×1025 м -3.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение коэффициента динамической вязкости жидкости. Каков его физический смысл? В каких единицах он из меряется в СИ и СГС? 2. В чем состоит физический смысл понятия "градиент скорости"? 3. Какова природа внутреннего трения в газах? 4. От чего зависит коэффициент вязкости? 5. Покажите, что для газов 6. Выведите формулу силы внутреннего трения. 7. Что называется длиной свободного пробега газа? 8. Как средняя длина свободного пробега молекул зависит от давления газа?
Лабораторная работа №10 ИЗУЧЕНИЕ ЗАВИСИМОСТИ КИНЕМАТИЧЕСКОЙ ВЯЗКОСТИ ОТ ТЕМПЕРАТУРЫ
Цель работы: Экспериментальное определение коэффициента кинематической вязкости исследуемой жидкости и его зависимость от температуры, а также оценка энергии активации вязкого течения. Приборы и принадлежности: Вискозиметр, термостат, секундомер, термометр, ручной насос, исследуемые жидкости.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Из закона Пуазейля, описывающего ламинарное течение жидкости по трубам (капиллярам)
Следует:
где h – коэффициент динамической вязкости, t – время протекания объема V жидкости через трубу радиуса r и длинны l при давлении на концах трубы D p. Если жидкость из трубы вытекает под действием силы тяжести, то D p = r gh, (3) где r – плотность жидкости, g – ускорение свободного падения. Наряду с понятием динамической вязкости h используется понятие кинематической вязкости n, которая определяется как отношение коэффициента динамической вязкости к плотности жидкости:
Из (2) и (3) для этого коэффициента мы имеем:
т.е. n прямо пропорционален времени протекания жидкости объема V через трубу. Этим пользуются при экспериментальном определении кинематической вязкости жидкости. Для ее определения служит прибор, называемый вискозиметром (см. описание прибора в разделе 3.6). Коэффициент пропорциональности между n и t в формуле (5) зависит от конструкции вискозиметра и является постоянным для данного прибора. Его численное значение определяется в заводских условиях. Тогда формула (5) для конкретного вискозиметра примет вид: n = С×t, (6) где С = p gr 4/8 V – постоянная вискозиметра. Единица измерения кинематической вязкости в системе СГС – стокс (1 Ст = 1 см 2/ с), используется также дольная единица стокса – сантистокс (1 сСт = 1×10–2 Ст). В системе СИ единица измерения – 1 м 2/ с = 104 Ст = 106 сСт. Вязкость жидкостей, в отличие от газов, сильно зависит от температуры. Эта зависимость для не очень больших перепадов температуры может описываться приближенной формулой:
где А и W – некоторые постоянные, определяемые на опыте, Т – абсолютная температура, k – постоянная Больцмана. Величина W имеет физический смысл энергии активации вязкого течения, т.е. энергии образования молекулярной полости, в которую проскакивает данная молекула, сорвавшись после некоторого числа колебаний со своего временного положения равновесия. Пусть при Т = Т 0, n = n 0
Деля (8) на (7), имеем:
Прологарифмируем:
Обозначим:
В результате имеем линейную зависимость вязкости жидкости от температуры в переменных x, у с угловым коэффициентом Экспериментальная проверка закона (7) или (10) и определение энергии активации W являются целью настоящей работы. Установка для изучения зависимости вязкости жидкости от температуры состоит из вискозиметра, установленного в стеклянном сосуде. Для измерения температуры жидкости в вискозиметре через сосуд пропускают воду, нагреваемую в термостате. Устройство термостата и вискозиметра, а также правила работы с ними см. разделе 3.
ИЗМЕРЕНИЯ И ОБРАБОТКА ИХ РЕЗУЛЬТАТОВ
1. Чтобы температура сравнялась во всем объеме стеклянного сосуда, перед началом работы на 5 – 10 минут включите электродвигатель термостата. 2. Убедитесь, что в вискозиметре имеется необходимое количество исследуемой жидкости. 3. С помощью резинового шланга подсоедините ручной насос к отводу 7 вискозиметра (рис. 37). 4. Отметьте по термометру, вставленному в стеклянный сосуд, температуру t 0 с точностью до 0.1°С. 5. Закрыв пробкой отверстие 8, осторожно накачайте насосом жидкость, чтобы она поднялась выше отметки 2 вискозиметра, после чего откройте отверстие 8. 6. В момент, когда уровень вытекающей жидкости поравняется с меткой 2, включите секундомер и выключите его, когда этот уровень будет проходить метку 3. Снимите отсчет времени t 0. 7. По формуле (6) вычислите начальное значение вязкости жидкости n 0 при t 0 (постоянная С вискозиметра указана на корпусе прибора). 8. Включите нагреватель термостата и подогрейте воду примерно на 5°С. Для перемешивания воды включите электродвигатель. 9. После того, как температура воды достигнет нужного значения t 1, отключите нагреватель при включенном электродвигателе и выждите 5–10 мин, чтобы вода в сосуде перемешалась, а вискозиметр прогрелся. 10. Отключите электродвигатель, накачайте жидкость в вискозиметр согласно п. 5 и, заметив точно значение температуры t 1, измерьте время протекания жидкости t от отметки 2 до 3, как было описано выше. 11. Снимите не менее 6-ти измерений, увеличивая температуру на 5°С. Результаты измерений и вычислений занесите в таблицу 12. Таблица 12
12. По данным таблицы постройте график у = f (х) на листе миллиметровой бумаги. Аппроксимируйте полученный график прямой линией. 13. По графику определите угловой коэффициент a и рассчитайте энергию активации вязкого течения по формуле W = a kT 0 14. Зная величину a, рассчитайте по формуле
коэффициент кинематической вязкости при других произвольно выбранных температурах в интервале от 0° до 100°С (вычислите не менее 10 значений), заполните таблицу 13. По полученным данным на миллиметровке постройте график зависимости у = f (х) для интервала Таблица 13
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение коэффициента динамической и кинематической вязкости жидкости. 2. В каких единицах измеряется h и n в системе СИ и СГС? 3. Расскажите о принципе работы вискозиметра. 4. Чем объясняется наличие сил внутреннего трения в жидкостях? 5. Выведите формулу Пуазейля. 6. Почему скорость слоя жидкости, прилегающего к стенкам капилляра, равна нулю? 7. Расскажите о структуре жидкости и ее свойствах. Что такое "ближний порядок", "среднее время оседлой жизни", "энергия активации"? 8. Почему вязкость жидкости убывает с ростом температуры?
Лабораторная работа №11 Определение коэффициента поверхностного натяжения методом отрыва кольца
Цель работы: Экспериментальное измерение коэффициента поверхностного натяжения жидкости методом отрыва кольца от поверхности исследуемой жидкости. Приборы и принадлежности: технические весы с разновесом, штангенциркуль, металлическое кольцо, кювета с исследуемой жидкостью.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Сущность метода состоит в том, что измеряются силы, которые необходимо приложить, чтобы оторвать тонкое металлическое кольцо от поверхности жидкости. Внешний вид установки представлен на рис. 16. Она представляет собой штатив, на которой укреплены весы В и подвижный столик для кюветы с исследуемой жидкостью Д. На левой чашке весов укреплен крючок К для подвешивания колец разного диаметра. Конструкция столика позволяет перемещать его и закреплять на разной высоте с помощью зажима С и, кроме того, плавно менять высоту с помощью винта А.

Рис. 16 Рис. 17 Отрыв (а точнее, разрыв поверхности) происходит по двум окружностям, диаметры которых D и d равны внешнему и внутреннему диаметрам кольца (рис. 17). Общая длина линии разрыва l = pD + pd. (1) Обозначая толщину стенок кольца через h, имеем: d = D - 2h. (2) Подставив последнее выражение (2) в выражение (1) вместо d, находим: l = 2p(D - h). (3) Коэффициент поверхностного натяжения s численно равен силе F, действующей на единицу длины произвольной линии l:
Тогда на основании (4) получаем расчетную формулу для определения s:
ИЗМЕРЕНИЯ И ОБРАБОТКА ИХ РЕЗУЛЬТАТОВ
1. Измерьте штангенциркулем внешний диаметр D и толщину h кольца. 2. Подвесьте кольцо к левой чашке весов, как показано на рис. 16. Уравновесьте весы с помощью песка. Песок насыпается совком мелкими порциями, чтобы не пропустить момент уравновешивания. 3. Отпустив зажим С, поднесите чашку с жидкостью к кольцу до его соприкосновения с поверхностью жидкости. Закрепите зажим С. Затем, плавно вращая винт А, опустите немного чашку с жидкостью так, чтобы весы вышли из состояния равновесия, и это было бы заметно глазом. Кольцо при этом должно удерживаться в воде силами поверхностного натяжения. 4. Осторожно насыпьте на вторую чашку весов столько песка, чтобы кольцо вышло из жидкости, преодолев силу поверхностного натяжения. Песок насыпается совком мелкими порциями, чтобы не пропустить момент отрыва кольца. 5. Отодвиньте столик в сторону. Осушите кольцо фильтрованной бумагой и уравновесьте весы с помощью гирь. Их вес, очевидно, равен силе поверхностного натяжения F. 6. Вычислите коэффициент s по формуле (5). Опыт произведите 3-5 раз. 7. Результаты измерений и вычислений занесите в таблицу 14: Таблица 14
Примечание: Если колец несколько, то в таблицу следует добавить следующие колонки для записи данных, и усреднения результатов производить для всех колец. 8. Запишите окончательный результат в виде:
где s ср – среднее значение s для всех опытов, Ds ср – среднеквадратичная погрешность измерения s.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какова природа сил поверхностного натяжения? 2. Дайте несколько определений коэффициента поверхностного натяжения (КПН); покажите, что они эквивалентны. 3. В каких единицах измеряется КПН? Каков его физический смысл? 4. Какое направление имеют силы поверхностного натяжения? Сделайте рисунок к вашему ответу. 5. Чем объясняется тот факт, что при отсутствии внешних сил жидкость принимает форму шара? 6. Почему большая капля жидкости, лежащая на не смачиваемой поверхности, сплющивается сильнее, чем маленькая при наличии сил тяжести? 7. На сколько градусов нагревается капля воды, которая получилась от слияния пяти исходных капель радиусом по 1 см каждая (это происходит в условиях невесомости)? 8. В чем заключается опыт Плато? 9. Объясните, почему смазанная жиром иголка может удерживаться на поверхности воды? 10. Выведите расчетную формулу (5).
Лабораторная работа №12 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ МЕТОДОМ ПОДНЯТИЯ ЖИДКОСТИ В КАПИЛЛЯРАХ
Цель работы: Экспериментальное определение коэффициента поверхностного натяжения методом поднятия жидкости в капиллярных трубках с применением высокоточного оптического прибора – катетометра. Приборы и принадлежности: катетометр КМ-10, набор капиллярных трубок, стакан для жидкости, держатель со штативом, термометр.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
При соприкосновении с твердым телом поверхность жидкости получает некоторую кривизну. Силы поверхностного натяжения дают при выпуклых и вогнутых поверхностях слагающую, направленную всегда в сторону вогнутой поверхности, и, таким образом, создают под всякой искривленной поверхностью добавочное давление: избыточное, если поверхность выпуклая, или недостаточное, если она вогнутая. Для сферической поверхности добавочное давление может быть выражено следующим образом:
где D p – добавочное давление, R – радиус кривизны поверхности, s – коэффициент поверхностного натяжения (КПН). Добавочным давлением, обусловленным кривизной мениска, вызываются поднятие и опускание жидкости в капиллярах. Жидкость опускается или поднимается в капилляре настолько, чтобы гидростатическое давление столба жидкости уравновесило это давление. Если считать, что жидкость полностью смачивает поверхность трубки, то радиус кривизны R совпадает с внутренним радиусом трубки r, тогда
где r – плотность жидкости, g – ускорение свободного падения, h – высота подъема жидкости в капилляре. Таким образом, зная радиус капилляра, плотность жидкости и высоту ее подъема в капилляре, можно по формуле (2) определить КПН. В работе используется набор из трех соединенных между собой трубок (Рис. 18), причем две из них являются рабочими капиллярами, а третья служит для заполнения первых двух жидкостью.
Рис. 18 После того, как в капилляры наливается жидкость, в каждом из них устанавливается определенный уровень. Допустим, что уровни поднятия жидкости в капиллярах измеряются относительно уровня в широкой трубке. Тогда в соответствие с формулой (2)
Отсюда
Окончательная формула для расчета приобретает вид:
Основным элементом экспериментальной установки для определения КПН является катетометр. Катетометры служат для измерения вертикальных расстояний на недоступных для непосредственного измерения объектах. С устройством и настройкой катетометра необходимо ознакомиться по описанию, прилагаемому к данному прибору (см. раздел 3.7).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2029; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.26.141 (0.013 с.) |

 , (16)
, (16)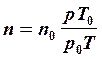 , (17)
, (17) . (18)
. (18) . Результаты измерений и вычислений представьте в виде таблицы 11.
. Результаты измерений и вычислений представьте в виде таблицы 11. .
. . (1)
. (1) , (2)
, (2) . (4)
. (4) , (5)
, (5) , (7)
, (7) . (8)
. (8) .
. . (9)
. (9)
 ;
;  и для этих обозначений, согласно (9), получим:
и для этих обозначений, согласно (9), получим: . (10)
. (10)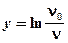
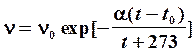 ,
, .
.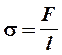 . (4)
. (4) . (5)
. (5) Н/м,
Н/м,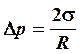 , (1)
, (1) , (2)
, (2)
 ,
,  .
. .
. . (4)
. (4)


