
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерения и обработка их результатовСодержание книги Поиск на нашем сайте
1.Изучите по описанию устройство катетометра, методику его настройки и измерений. 2.Установите в штативе и укрепите горизонтально набор трех капиллярных трубок. Измерьте с помощью катетометра внутренний диаметр каждой трубки в трех различных сечениях, взяв за результат среднее арифметическое значение. Перед измерением трубки должны быть чисто вымыты и просушены. 3.Затем установите и укрепите капилляры в штативе вертикально открытыми концами вверх. 4.С помощью пипетки заполните через широкую капиллярную трубку набор капилляров исследуемой жидкостью. Затем измерьте уровень жидкости в каждой трубке, снимая отсчет высоты по шкале катетометра. Значение высоты снимать по нижней части мениска. 5.Проведите не менее трех измерений уровней в каждой трубке при различном их заполнении жидкостью в соответствии с предыдущим пунктом. 6.Используя табличные значения r и g рассчитайте s, s ср, D s. 7.Данные измерений и вычислений занесите в таблицу 15: Таблица 15
8.Запишите результаты вычислений в виде: s = sср ± Ds (Н / м).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какова природа сил поверхностного натяжения? 2. В каких единицах измеряется КПН? 3. В чем заключаются капиллярные явления? Приведите примеры их проявления в природе и применения в практике. 4. Выведите формулу Жюрена, по которой вычисляется высота подъема жидкости в капиллярах. 5. Объясните, почему возникают значительные силы сцепления между смоченными водой и соединенными вместе стеклянными пластинами. 6. Для чего предназначен катетометр и как с ним работать?
Лабораторная работа №13 изучение температурной зависимости коэффициента ПОВЕРХНОСТНОГО НАТЯжеНИя ЖИДКОСТИ МЕТОДОМ МАКСИМАЛЬНОГО ДАВЛЕНИЯ В ПУЗЫРЬКАХ
Цель работы: экспериментальное определение коэффициента поверхностного натяжения жидкости и его зависимость от температуры. Приборы и принадлежности: термостат, пробирка с капилляром, аспиратор, жидкостный манометр, термометр, стакан для жидкости.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Давление внутри пузырька, возникшего на конце капилляра в жидкости при слабом прохождении воздуха через этот капилляр, равно атмосферному давлению p 0. Это давление уравновешивается давлением p над поверхностью жидкости в сосуде и давлением р 1, обусловленным поверхностным натяжением. При небольшом погружении капилляра в жидкость гидростатическим давлением можно пренебречь, тогда
p 0 = p 1 + p,(1) где
При R = rp 1 – максимально (R – радиус пузырька, r - радиус капилляра. Следовательно,
Величина
постоянна для данного капилляра, ее можно определить, используя известное значение радиуса капилляра, или измерив ее с помощью катетометра. Зная k, можно по разности давлений внутри и вне пузырька определить величину КПН:
С повышением температуры КПН уменьшается, так как при критической температуре он должен быть равен нулю. При этой температуре исчезает разница между жидкостью и ее паром, а значит, исчезает и поверхность, разделяющая обе фазы. Однако точный вид зависимости КПН от температуры не может быть установлен теоретически. Приближенно зависимость КПН от температуры выражается следующим равенством:
где В – постоянный коэффициент, определяемый из опыта, r – плотность жидкости, m – молярная масса, t – небольшая величина размерности температуры. Из формулы (4) видно, что зависимость КПН от температуры тем сильнее, чем больше плотность жидкости и чем меньше молекулярная масса. Коэффициент В практически одинаков для всех жидкостей и равен 2.1 (в системе единиц СГС). Экспериментальная установка для определения коэффициента поверхностного натяжения жидкостей (рис. 19) состоит из сосуда 1 с исследуемой жидкостью, внутри которого вставлен капилляр 2. Сосуд 1 с помощью системы трубок соединен с аспиратором 3. Если из аспиратора вытекает вода, то давление воздуха внутри сосуда 1 понижается, а при некотором его значении p под действием атмосферного давления p 0 через капилляр в жидкость продавливается пузырёк воздуха. Разность давления p 0 ‑ p измеряется манометром 4. Для исследования зависимости КПН от температуры сосуд 1 помещают в стакан 5, заполненный водой, которая подогревается электрическим нагревателем 6. Температура в стакане 5 измеряется термометром 7. Аспиратор снабжен краном 8, через который вытекает вода. Нагреватель через тумблер 9 подключен к сети 42 В.
Рис. 19
ИЗМЕРЕНИЯ И ОБРАБОТКА ИХ РЕЗУЛЬТАТОВ
1. Наполните водой аспиратор. 2. Установите в сосуде 1 капилляр так, чтобы он касался поверхности исследуемой жидкости. 3. Откройте кран 8 (см. рис. 19) так, чтобы на конце капилляра медленно, ритмично появлялись пузырьки воздуха. 4. Определите для этого режима максимальную разность уровней (см. рис. 19) в манометре, которая равна разности давлений D p (1 мм. вод. ст. = 9.8 Па). Измерьте также температуру жидкости. 5. Определите коэффициент k. 6. По формуле (3) рассчитайте s, заполните таблицу 16 7. По мере повышения температуры изменения s проводите через 5-10 0С (перед измерением необходимо отключить нагреватель и выждать 5 мин; всего необходимо провести не менее семи измерений).
Таблица 16
8. Постройте график зависимости s = ¦ (t). Аппроксимируйте экспериментальные точки линией вида (4), вычислите коэффициент B и величину t.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что называется коэффициентом поверхностного натяжения жидкости? В каких единицах он измеряется? 2.Как зависит коэффициент поверхностного натяжения от температуры? Когда и почему он равен нулю? 3.Какая жидкость называется смачивающей, какая - несмачивающей? Приведите примеры. 4.Что такое "краевой угол"? 5.Выведите формулу Лапласа. Чему равно дополнительное давление в случае цилиндрической поверхности, плоской поверхности? 6.Чем обусловлено внутреннее давление в жидкости? 7.Выведите формулу Жюрена. 8.Чему равно давление в пузырьке воды, находящемся на глубине 50 см от поверхности жидкости, если его радиус равен 0.5 см.
Лабораторная работа №14 ИЗУЧЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ В ИЗОЛИРОВАННОЙ СИСТеме
Цель работы: исследование приращения энтропии в необратимых адиабатных процессах. Приборы и принадлежности: калориметр с мешалкой, нагреватель, термометр с ценой деления 0.1°С, бачок с водой, мензурка вместимостью 100–150 мл, набор из пяти исследуемых образцов: №1 – свинцовый, №2 – медный, №3 – стальной, №4 – алюминиевый, №5 – оловянный; весы технические, набор гирь.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Для описания поведения термодинамических систем Клаузиус ввел функцию параметров состояния S, названную им энтропией. Для вычисления изменения энтропии D S рассматриваемый процесс делится на достаточно малые участки, в пределах которых температуру Т системы можно считать постоянной. Элементарное приращение энтропии dS на таком участке приравнивается приведенному количеству теплоты dQ/T, сообщенному при этом системе или отнятому от нее:
Полное изменение энтропии в каком–либо процессе вычисляется путем интегрирования ее элементарных приращений dS по всему процессу от начального состояния 1 до конечного 2:
где dQ – элементарный приток теплоты в систему, Т – термодинамическая температура системы. При вычислениях подынтегральное выражение (1) и пределы интегрирования преобразуют с помощью величин, характеризующих рассматриваемый процесс. Пользуясь понятием энтропии, основное содержание второго начала термодинамики можно сформулировать следующим образом: любой процесс в изолированной системе подчиняется условию: D S ³0, (2) где D S – изменение энтропии системы, при этом, если процесс обратим, в выражении (2) имеет место знак равенства, если необратим – знак неравенства. Таким образом, D S в изолированной системе может служить мерой необратимости протекающих в ней процессов: чем меньше D S, тем ближе процесс к обратимому. В данной работе предлагается измерить изменение энтропии изолированной системы, в которой происходит необратимый процесс теплообмена. Схема экспериментальной установки приведена на рис. 20. Она включает в себя исследуемый образец 1, опущенный посредством пробки 7 в сосуд с водой 3, нагреваемый при помощи электроплитки 2. Теплообмен происходит при перенесении и опускании исследуемых образцов, нагретых до одной и той же температуры Т (температуры кипящей воды по шкале Кельвина), из сосуда 3 в воду, находящуюся в калориметре 4 при температуре Т 1. Наличие внешнего стакана калориметра делает систему практически изолированной. В теплообмене участвуют четыре тела: 1. Испытуемый образец массой m т , удельной теплоемкостью c т , и начальной температурой Т = 373 К. 2. Стакан калориметра массой m к, удельной теплоемкостью c к и начальной температурой Т 1. 3. Мешалка 6 (рис. 20) массой m м, удельной теплоемкостью c м и начальной температурой Т 1. 4. Вода, находящаяся в калориметре, имеет массу m в, удельную теплоемкость c в и начальную температуру T 1.
Р и с. 20 После теплообмена установится температура Т 0. При этом энтропия каждого из тел изменится следующим образом: для первого тела для второго тела для третьего тела для четвертого тела Учитывая свойство аддитивности энтропии, можно рассчитать изменение энтропии всей системы:
По этой формуле проводятся расчеты.
ИЗМЕРЕНИЯ И ОБРАБОТКА ИХ РЕЗУЛЬТАТОВ
1.Определите при помощи технических весов массы исследуемых образцов m Т, калориметра m К, мешалки m М. 2.Налейте в сосуд 3 наполовину воды и поместите в него исследуемый образец известной массы. Образец на шнуре закрепляется при помощи пробки, вставляемой в крышку сосуда 3. 3.Поставьте сосуд на электрическую плитку и включите ее в сеть. 4.Налейте в стакан калориметра 4 100 мл воды, отмерив нужный объем мензуркой. 5.Через 5 минут после того, как вода в нагревателе закипит, измерьте температуру воды Т 1 в калориметре. 6.Затем быстро перенесите и опустите исследуемый образец в калориметр, закрыв его крышкой. Оставьте его подальше от нагревателя и следите за повышением температуры воды по термометру 5. 7.Когда рост температуры замедлится, сделайте 4–5 перемешиваний при помощи мешалки. Отсчитайте наибольшее значение температуры T 0. 8.По измеренным данным, пользуясь формулой (3), найдите изменение энтропии. Теплоемкости калориметра c К и мешалки с М принять равными 896 Дж/(кг×К) (алюминий). Результаты измерений и вычислений занесите в таблицу 17. Таблица 17
9.Вылейте воду из калориметра и дайте ему охладиться. Для ускорения охлаждения можно воспользоваться водой комнатной температуры. Повторите измерения с другими телами (масса воды во всех опытах должна быть одинаковой m В = 100 г. 10.Постройте график зависимости D S от молярной теплоемкости испытуемых тел C = с Т,× m Т, сделайте выводы. Для определения молярной массы m Т испытуемых образцов воспользуйтесь периодической системой химических элементов.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Приведите различные формулировки второго начала термодинамики. 2.Дайте определение энтропии. В чем ее статистический смысл? 3.Какие процессы называют обратимыми и необратимыми, равновесными и неравновесными? 4.Энтропию как и энергию называют функцией состояния. Что это значит? 5.Составьте уравнение теплового баланса для исследуемой термодинамической системы, пользуясь экспериментальными данными, полученными по одному из предложенных образцов. 6.Изобразите обратимый цикл Карно в диаграмме T – S и получите выражение для его термического КПД.
Лабораторная работа №15 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЯ ТЕРМОЭЛЕКТРОНОВ ПО СКОРОСТЯМ
Цель работы: экспериментальное исследование распределения Максвелла. Приборы и принадлежности: электронная лампа – пентод 6П9, два выпрямителя ВУП–2, микроамперметр М136, три вольтметра, два резистора.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
В замкнутом сосуде, наполненном газом, при температуре Т устанавливается термодинамическое равновесие, которое характеризуется определенным распределением молекул по скоростям. Среднее число молекул в единице объема
В зависимости от выбранной системы координат функция dP (V) имеет различный вид. В декартовой системе компонентов скоростей:
в цилиндрической системе:
в сферической системе:
Здесь А – нормировочная константа, Константа A в уравнении (2) определяется в результате интегрирования dP (V) по всем возможным значениям любой из компонентов скоростей V x, V y, V z от –¥ до +¥. Учитывая условие нормировки (интеграл dP (V) должен равняться 1, что означает: любая наугад взятая молекула имеет какую-нибудь скорость):
определим константу А 1 для компонента скорости V x. Она равна
Очевидно, что нормировочные константы для других компонент скоростей V y V z также будут равны А 1 вследствие хаотического, движения молекул (любое направление движения молекулы является равновероятным). Из математики известно, что вероятность сложного события равна произведению вероятностей каждого из событий в отдельности, тогда A = A1 3и решение выражения(2) будет иметь вид:
Величина
представляет собой функцию распределения молекул по скоростям (распределение Максвелла). Она определяет долю молекул единицы объема газа, скорости которых заключены в интервале скоростей, равном единице, включающем данную скорость (плотность вероятности распределения скоростей). Для решения различных задач удобно пользоваться формулой Максвелла, выраженной через относительные скорости:
Здесь u = V/Vн – относительная скорость, В данной работе для исследования вида функции распределения предлагается метод задерживающего потенциала. Суть метода состоит в следующем. Известно, что электронный газ, который образуется в пространстве между катодом и управляющей сеткой электронной лампы вследствие термоэлектронной эмиссии, подчиняется статистике Максвелла. Электронный газ имеет температуру катода. В многоэлектродной лампе типа пентода электронное облако из-за конструктивных особенностей лампы обладает
Рис. 21 Рис. 22
осевой симметрией (катод представляет собой тонкий нагретый цилиндр). Для описания статистических свойств электронного газа в этом случае удобно применять формулу (3). Если электроны, вылетающие из облака, заставить проходить через задерживающее радиальное электрическое поле, то при некоторой разности потенциалов U 3 преодолеть влияние поля могут только те электроны, у которых радиальная составляющая скорости удовлетворяет условию:
где e – заряд электрона, V r – радиальная составляющая скорости. Определим число электронов, пролетающих через тормозящее поле в единицу времени, т.е. возникающий ток. Пользуясь формулами (1) и (3), определим число электронов, имеющих значение радиальной составляющей скорости в интервале [ V r; V r + dV r]. Интегрируя (1) с учетом выражения (3) по азимутальному углу f в пределах от 0 до 2 p и по компоненте скорости V z от –¥ до +¥, получим:
Число электронов
Наконец, число электронов
Из (13) видно, что общее число электронов, пролетающих в единицу времени через тормозящее поле, равно интегралу с переменным нижним пределом от выражения, совпадающего с точностью до постоянной с распределением Максвелла (7). При этом ток, идущий через лампу, будет пропорционален Меняя значение задерживающей разности потенциалов, можно получить функцию В настоящей работе распределение Максвелла проверяется на установке, схема которой приведена на рис. 22. В качестве электронной лампы применяется пентод 6П9. Электронное облако образуется в пространстве "катод – управляющая сетка", потенциалы которых практически одинаковы. Между сетками G1, и G2 с помощью выпрямителя ВУП–2 создается тормозящее поле. Величина U з может меняться в пределах от 0 до 30 В. Питание накала катода осуществляется напряжением 6.3 В и контролируется вольтметром V1. Для измерения U з служит вольтметр V3. Электроны, пролетающие пространство с тормозящим полем, проходят затем ускоряющее поле между анодом и последней сеткой G3. Ускоряющая разность потенциалов обеспечивается работой выпрямителя ВУП–2. Разность потенциалов между анодом и сеткой G3 подбирается так, чтобы обеспечить в анодной цепи ток насыщения. При этом все электроны, скорость которых превышает V r0, попадают на анод. Анодное напряжение регистрируется в работе вольтметром V2, а анодный ток – микроамперметром типа M–136. Между сетками G2 и G3 включен резистор R2, сопротивление утечки которого 5 МОм, а сопротивление резистора R1, включенного между катодом и сеткой G1, равно 200 Ом. Описанная схема включения позволяет свести к минимуму влияние изменения разности потенциалов между сетками G1, и G2 на плотность электронов в околокатодном пространстве, что существенно при проверке закона распределения по скоростям. Кроме того, при такой схеме включения пентода минимально взаимное влияние источников питания в анодной цепи и в цепи, где создается задерживающая разность потенциалов.
ИЗМЕРЕНИЯ И ОБРАБОТКА ИХ РЕЗУЛЬТАТОВ
Включение экспериментальной установки в работу осуществите в следующей последовательности: 1. Изучите расположение приборов и средства управления ими по надписям, нанесенным на панели установки. Установите все переключатели и ручки управления рабочих пределов приборов в положение "Откл.". 2. Включите шнур питания установки в розетку 220 В, установленную на лабораторном столе. Тумблер питания на панели установки включить в положение "Сеть", при этом должна гореть сигнальная лампочка. 3. Установите переключатель "Питание накала" в положение "норма", при этом вольтметр V1 должен показывать 6.3 В. 4. Ручку управления выпрямителя ВУП–2 "Анодное напряжение" установите на отметку 140 В, контролируя показание по вольтметру V2. 5. Переключатель вольтметра V3, измеряющего задерживающее напряжение U з, поставьте в положение множителя х2. При этом предел измерения вольтметра будет равен 10 В, а цена наименьшего деления шкалы прибора – 0.2 В. Вращая ручку регулятора задерживающего напряжения по часовой стрелке (направление "меньше) установите стрелку вольтметра на 0. 6. Переключатель микроамперметра M136, измеряющего анодный ток, установите в положение множителя х10. При этом предал измерения микроамперметра равен 50 мкА, а цена наименьшего деления шкалы прибора – 0.5 мкА. 7. После этих операций дайте установке прогреться 5 мин и она готова к съему экспериментальных данных.
Задание 1. Исследование экспериментальной зависимости Плавно вращая ручку регулятора задерживающего напряжения против часовой стрелки, изменяйте задерживающее напряжение U з от 0 до 10 В, причем в интервале от 0 до 2.4 В – через 0.2 В, в интервале от 2.4 до 4 В – через 0.4 В, в интервале от 4 до 10 В – через 1 В. Для каждого значения задерживающего потенциала фиксируйте анодный ток по микроамперметру М136. Внимание! При измерении следите за тем, чтобы стрелка микроамперметра по возможности находилась в середине шкалы. Для этого своевременно меняйте предел измерения микроамперметра. Результаты измерений занесите в таблицу 18. Таблица 18
Постройте по экспериментальным точкам на миллиметровой бумаге график
Экспериментальные точки аппроксимируйте плавной интегральной кривой. Задание 2. Исследование распределения термоэлектронов по скоростям. Графически дифференцируя функцию (14), постройте график функции
которая с точностью до масштабных множителей должна совпадать с формулой распределения Максвелла (8). Для проверки этого утверждения необходимо сравнить полученную кривую (15) с теоретической кривой плотности вероятностей распределения скоростей Максвелла (9), выраженной через относительные скорости, график которой приведен на рис. 21. Учитывая, что сравниваемые кривые (15) и (9) построены в разных масштабах, необходимо произвести нормировку переменных экспериментальной функции (15) как по оси абсцисс, так и по оси ординат. Так как на рис. 21 по оси абсцисс отложены значения U = V / V н, где
где значение При нормировке по оси ординат максимуму функции Графическое дифференцирование, нормировку и построение графиков проведите на основе данных таблицы 18, заполнив вычисляемыми значениями величин таблицу 19. Внимание! При вычислении значений Таблица 19
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. При каких предположениях справедливо распределение Максвелла по скоростям? 2. Начертите график функции распределения f (V) молекул по модулям скоростей. Как изменится этот график с увеличением температуры? Каков физический смысл площади, ограниченной графиком этой функции и осью абсцисс V? 3. Получите выражение (9). Чем удобна эта форма записи распределения скоростей по Максвеллу? 4. Чему равны: среднее значение скорости, среднее значение квадратичной скорости, значение наивероятнейшей скорости для молекул идеального газа? Как применить закон Максвелла для вычисления значений перечисленных скоростей? 5. Какие существуют экспериментальные методы для проверки распределения Максвелла?
Лабораторная работа №16 ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ЖИДКОСТИ ЭЛЕКТРОКАЛОРИМЕТРИЧЕСКИМ МЕТОДОМ
Цель работы: определение водяного эквивалента калориметра и удельной теплоёмкости неизвестной жидкости. Приборы и оборудование: электрокалориметр с термометром, вольтметр, соединительные провода, ключ, неизвестная жидкость, секундомер, лупа, амперметр.
ТЕОРИЯ МЕТОДА И ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Калориметрический метод определения удельной теплоёмкостёй жидкости основан на следующем: термодинамической системе, состоящей из сосуда с двойными стенками (калориметра) и налитой в него жидкости, сообщается известное количество теплоты, вследствие чего температура этой системы повышается. Можно написать уравнение теплового баланса: Q = mc D T + W D T + Q ¢, (1) где: Q – количество теплоты, сообщенное системе, с – удельная теплоёмкость жидкости, m – масса жидкости, W – водяной эквивалент калориметра, определяемый как теплоёмкость калориметра, D Т – изменение температуры, Q ¢ – тепловые потери. Из этого уравнения можно выразить с и определить её, зная остальные величины. В данной работе энергия сообщается системе с помощью электронагревателя, а количество теплоты вычисляется с помощью закона Джоуля-Ленца: Q = Iut, (2) где: U – напряжение, I – сила тока в цепи, t - время прохождения электрического тока по спирали нагревателя. Измерения выполняются дважды: первый раз с известной жидкостью (водой) для определения водяного эквивалента; второй раз – для определения собственно удельной теплоёмкости неизвестной жидкости. Электрокалориметр состоит (рис. 23) из внешнего стакана 1, прикрученного к основанию 2. Внутрь вставляется второй стакан 3, который закрывается крышкой 4. В крышку встроены термометр 5, мешалка 6, спираль 7 с клеммами 8. Нагреватель подключается к источнику напряжения по схеме, представленной на рис. 24.
Рис. 23 Рис. 24 Учёт тепловых потерь Q ¢ в формуле (1) осуществляется следующим образом: - жидкость нагревается незначительно, на 3 - 5 градусов; - опыты по определению водяного эквивалента и удельной теплоёмкости жидкости проводятся в одинаковых условиях. При этом тепловые потери в обоих случаях будут одинаковы и они автоматически учитываются при определении W. Для первого случая имеем:
отсюда
где с в и m в – удельная теплоемкость и масса воды в калориметре. Для второго случая
отсюда
где: c и m – удельная теплоёмкость и масса неизвестной жидкости.
ИЗМЕРЕНИЯ И ОБРАБОТКА ИХ РЕЗУЛЬТАТОВ
1. Определить массу m 0 пустого калориметра вместе с крышкой, основанием, термометром и мешалкой. Взвешивать нужно не менее трех раз и брать среднее значение. 2. Налить во внутренний стакан калориметра воды на 3/4 объёма. Определить m 1. 3. Для установления термодинамического равновесия выдержать 5 минут, вращая время от времени ручку мешалки. Определить Т 1, пользуясь лупой. 4. Подключить калориметр к установке, а источник питания – к сети 42 В. Определить температуру Т 1 и сразу же одновременно включить секундомер и схему (замкнуть ключ). Зафиксировать U 1 и I 1. 5. После 7- 8 минут отключить схему и секундомер. Определить t 1. Перед определением T 1¢ выдержать 5 минут, вращая ручку мешалки. Примечание: При вращении ручки мешалки не держать калориметр руками, т.к. это ведет к снижению точности опыта. 6. Занести данные в таблицу 20 и рассчитать W по формуле (4). 7. Выполнить пункты 2-5, заменив воду на неизвестную жидкость и занести данные в таблицу 21. Примечание: Так как удельная теплоёмкость распространенных жидкостей примерно в 2 раза меньше удельной тепло- ёмкости воды, то время t 2 должно быть примерно в 2 раза меньше t 1, что обеспечивает одинаковые тепловые потери в обоих опытах. 8. Рассчитать с по формуле (6). 9. Вывести формулы для инструм
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.013 с.) |

 . (2)
. (2) .
.
 . (3)
. (3) . (4)
. (4)
 .
. , (1)
, (1)
 ;
; ;
; ;
; .
. . (3)
. (3) , скорость которых заключена между V и V + dV, равно произведению средней концентрации молекул идеального газа
, скорость которых заключена между V и V + dV, равно произведению средней концентрации молекул идеального газа  на вероятность dP (V) того, что скорость молекул лежит в интервале [ V; V + dV ]:
на вероятность dP (V) того, что скорость молекул лежит в интервале [ V; V + dV ]: . (1)
. (1) ; (2)
; (2) ; (3)
; (3) . (4)
. (4) – квадрат модуля скорости, остальные обозначения являются общепринятыми.
– квадрат модуля скорости, остальные обозначения являются общепринятыми.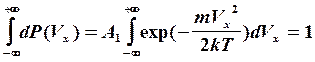 , (5)
, (5) . (6)
. (6) . (7)
. (7) . (8)
. (8) . (9)
. (9) – наивероятнейшая скорость, т.е. скорость, соответствующая вершине плотности распределения. Уравнение (9) – универсальное. В таком виде функция распределения не зависит ни от рода газа, ни от температуры. График функции распределения Максвелла для относительных скоростей представлен на рис. 21.
– наивероятнейшая скорость, т.е. скорость, соответствующая вершине плотности распределения. Уравнение (9) – универсальное. В таком виде функция распределения не зависит ни от рода газа, ни от температуры. График функции распределения Максвелла для относительных скоростей представлен на рис. 21.

 , (10)
, (10)
 . (11)
. (11) с радиальными скоростями, лежащими в интервале [ V r; V r + dV r], проходящих через единицу поверхности цилиндрического электрода в единицу времени, равно
с радиальными скоростями, лежащими в интервале [ V r; V r + dV r], проходящих через единицу поверхности цилиндрического электрода в единицу времени, равно  т.е.
т.е. (12)
(12) , пролетающих в единицу времени через пространство с запирающим потенциалом U з, определяется общим числом электронов, скорости которых превышают
, пролетающих в единицу времени через пространство с запирающим потенциалом U з, определяется общим числом электронов, скорости которых превышают  :
: . (13)
. (13) , производная которой по
, производная которой по  представляет собой распределение термоэлектронов по скоростям (8).
представляет собой распределение термоэлектронов по скоростям (8). .
. , В 1/2
, В 1/2
 . (14)
. (14) , (15),
, (15), отвечает максимуму функции, то при построении экспериментальной кривой вида (9) по оси абсцисс нужно отложить отношение (учитывая, что согласно (10) V r пропорциональна
отвечает максимуму функции, то при построении экспериментальной кривой вида (9) по оси абсцисс нужно отложить отношение (учитывая, что согласно (10) V r пропорциональна 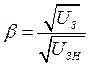 ,
, отвечает максимуму экспериментальной функции (15), т.е. наивероятнейшей скорости термоэлектронов.
отвечает максимуму экспериментальной функции (15), т.е. наивероятнейшей скорости термоэлектронов. следует приписать значение плотности вероятности, равное 0.83, что отвечает максимальному значению функции распределения Максвелла (9), если скорость выражается в относительных единицах. Произведя нормировку переменных, постройте на миллиметровой бумаге график экспериментальной функции f (b), аппроксимировав ее плавной кривой, и сравните ее с теоретической кривой f (u) (9). Построенные в одинаковом масштабе, они должны совпадать друг с другом в пределах точности эксперимента.
следует приписать значение плотности вероятности, равное 0.83, что отвечает максимальному значению функции распределения Максвелла (9), если скорость выражается в относительных единицах. Произведя нормировку переменных, постройте на миллиметровой бумаге график экспериментальной функции f (b), аппроксимировав ее плавной кривой, и сравните ее с теоретической кривой f (u) (9). Построенные в одинаковом масштабе, они должны совпадать друг с другом в пределах точности эксперимента. , В 1/2
, В 1/2




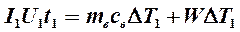 , (3)
, (3)  , (4)
, (4) , (5)
, (5) , (6)
, (6)


