
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение числа Авогадро методом растекания каплиСодержание книги
Поиск на нашем сайте
Оборудование: кювета, бюретка на штативе, линейка, раствор касторового масла или олеиновой кислоты.
Вопросы к допуску: 1. Какая физическая величина называется числом Авогадро? 2. Каким образом число Авогадро определяется в данной лабораторной работе?
Содержание и метод выполнения работы
Число Авогадро – это число молекул в моле любого вещества. Число Авогадро является одной из важнейших универсальных постоянных, значение которой используется при определении многих других постоянных величин (постоянной Больцмана, заряда электрона и т.д.). Существует до 20 различных методов определения числа Авогадро. Наиболее точное значение числа Авогадро получено на основании данных о плотности и строении кристаллов. Одним из первых методов определения числа Авогадро является метод Ж.Перрена, основанный на наблюдении распределения по высоте частиц, взвешенных в жидкости и совершающих броуновское движение.
Рассмотрим каплю некоторой жидкости 1, расположенную на поверхности другой, не смешивающейся с ней жидкости 2. Форма капли устанавливается в данном случае под влиянием трех сред: жидкости 1, жидкости 2, воздуха 3. Эти три среды имеют общую границу – окружность, ограничивающую каплю и пересекающую плоскость чертежа в двух точках. По этой окружности пересекаются между собой три поверхности: поверхность, разграничивающая, жидкость 2 и воздух 3 с коэффициентом поверхностного натяжения α23, поверхность, разграничивающая жидкость 1 и воздух 3 с коэффициентом поверхностного натяжения α13, поверхность, разграничивающая жидкости 1 и 2 с коэффициентом поверхностного натяжения α12. На каждую единицу длины контура (окружность диаметра АВ), разграничивающего все три среды, действуют силы поверхностного натяжения F23, F13, F12, численно равные соответственно значениям α23, α13, α12 (рис.2.8.). Эти силы будут направлены перпендикулярно к отдельным элементам окружности и касательно к соответствующим поверхностям раздела. В случае, когда можно пренебречь силой тяжести по сравнению с силами поверхностного натяжения, равновесной будет такая конфигурация капли, для которой: F23+F13+F12=0, или переходя от векторной суммы к алгебраической, получим: F23=F13cosθ13+F12cosθ12 отсюда следует, что в случае равновесия F23≤F13+F12, т.е. α23≤α13+α12, т.к. cosθ13 и cosθ12 меньше единицы. Если же F23>F13+F12, т.е. α23>α13+α12, то равновесие капли жидкости 1 на поверхности жидкости 2 невозможно, поэтому капля растекается по поверхности жидкости в виде пленки мономолекулярной толщины. Многие органические жидкости (эфир, скипидар, керосин) растекаются на поверхности воды. Для некоторых жидкостей (бензол, жирные кислоты, масло) явление растекания наблюдается только для первых капель, помещенных на поверхность воды. Последующие капли уже не растекаются, а остаются на поверхности воды в виде устойчивых капель. Это объясняется тем, что первые капли, растекаясь, загрязняют поверхности воды и уменьшают поверхностное натяжение настолько, что равновесие капель становится возможным. Многочисленные эксперименты, в частности опыты Ленгмюра, Дево, Релея и других, привели к выводу, что если площадь воды достаточно велика, то капля масла соответствующего объема растекается в очень тонкий мономолекулярный слой. Произведенные вычисления показали, что площадь, занимаемая каждой молекулой жирных кислот, равна: Sm=21´10-20м2. Молекулы жирных кислот представляют собой нечто вроде эллипсоида или цилиндра, и в мономолекулярном слое на поверхности воды они ”упакованы” вплотную, соприкасаясь боковыми поверхностями. Зная площадь, занимаемую одной молекулой, и измерив диаметр круга пятна на поверхности воды, можно рассчитать количество молекул в капле раствора: n=S/Sm, где S – площадь полученного круглого пятна: S=πd2/4. Отсюда для n получим выражение: Это же число молекул в капле можно найти, если известна масса олеиновой кислоты или касторового масла m, содержащейся в одной капле, и его молекулярная масса μ=0,282 n= где Ν0 – число Авогадро, а отношение
Из (2.9) получим для вычисления числа Авогадро формулу:
Порядок выполнения работы
1. В широкий сосуд (фотокювету) наливают чистую водопроводную воду. 2. Поверхность воды слегка посыпают тонким слоем талька. 3. На поверхность воды капают единственную каплю однопроцентного раствора олеиновой кислоты или какой-либо другой жирной кислоты. 4. Измеряют средний диаметр максимально расплывшегося масляного пятна. С этой целью измеряют диаметр пятна в шести различных направлениях и вычисляют среднеарифметическое значение. 5. Определяют путем взвешивания на аналитических весах массу бюкса m1. 6. Набирают в бюкс 3 капли раствора из той же бюретки и находят массу бюкса с раствором m2. 7. Вычисляют массу одной капли раствора: 8. Подставляют численное значение m в формулу (2.10) и вычисляют число Авогадро. Контрольные вопросы 1. В чем причина растекания капли жира по поверхности воды? 2. Выведите расчетную формулу, по которой определяется число Авогадро в данной лабораторной работе. 3. Какие способы определения числа Авогадро вам известны? 4. Где количество молекул больше: в 1г водорода или в 1г углекислого газа? III. ЯВЛЕНИЯ ПЕРЕНОСА В результате хаотического движения молекул и соударений между ними происходят непрерывные изменения их скоростей и энергий в веществе. Если в веществе существует пространственная неоднородность плотности, температуры или скорости упорядоченного движения отдельных слоев вещества, то на беспорядочное тепловое движение молекул вещества накладывается упорядоченное движение, которая ведет к выравниванию этих неоднородностей. Это движение называется явлением переноса. К явлениям переноса относится теплопроводность, внутреннее трение и диффузия. Во всех трех явлениях имеется много общего, а именно в среде происходит направленный перенос какой-либо величины (энергии, количества движения, массы) из одной части вещества в другую до тех пор, пока данная величина не распределится равномерно по всему объему. Явление теплопроводности состоит в направленном переносе энергии и возникает тогда, когда различные части среды имеют различную температуру, т. е. обладают различной внутренней энергией. Перенос тепла в теле происходит в направлении точек тела, имеющих более низкую температуру. Температура в различных точках тела является функцией координат точек В теории теплопроводности количество теплоты
где Градиент температуры показывает изменение температуры на единицу длины нормали к направлению движения тепла. Знак минус показывает, что энергия переносится в сторону убывания температуры Коэффициент теплопроводности Явление внутреннего трения (вязкости) наблюдается в телах при всех агрегатных состояниях, но большое практическое значение это явление имеет для жидкостей и газов. При движении жидкости или газа возникают силы внутреннего трения. Эти силы возникают вследствие того, что движение жидкости или газа слоистое и скорости перемещающихся слоев разные. Силы внутреннего трения направлены к уравниванию скорости движения всех слоев. Уравнивание слоев осуществляется путем передачи молекулами более быстрого слоя количества движения Таким образом, внутреннее трение обусловлено переносом количества движения
Градиентом скорости
Коэффициент вязкости или коэффициент внутреннего трения есть физическая величина, численно равная силе внутреннего трения, между двумя слоями с площадью, равной единице при градиенте скорости, равном единице. В СИ Знак минус в формуле Ньютона показывает, что перенос импульса направлен противоположно градиенту скорости движения слоев. Явление диффузии возникает тогда, когда состав среды в различных частях различен и заключается в самопроизвольном взаимном проникновении и перемешивании частиц двух соприкасающихся газов, жидкостей и твердых тел. Явление диффузии связано с направленным переносом массы вещества. Перенос массы вещества подчиняется первому закону Фика:
где
Коэффициентом диффузии ЛАБОРАТОРНАЯ РАБОТА №5 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ ЖИДКОСТИ КАПИЛЛЯРНЫМ ВИСКОЗИМЕТРОМ
Оборудование: прибор, пипетка, пикнометр, секундомер, исследуемые жидкости, термометр.
Вопросы к допуску: 1.Какое из явлений переноса изучается в данной лабораторной работе? В чем оно заключается? 2. На каком законе основывается определение коэффициента вязкости в данной лабораторной работе? 3. По какой формуле определяется коэффициент вязкости? 4. В каких единицах выражается коэффициент вязкости?
Содержание и метод выполнения работы
Для определения коэффициента вязкости жидкости используется закон Пуазейля для ламинарного течения по трубам (капиллярам):
где Пользуясь этим выражением, зная величины Однако удобнее пользоваться формулой Пуазейля для определения относительного коэффициента вязкости. В самом деле, если взять две жидкости (соответствующие величины для одной из них отметим знаком
Разделим второе уравнение на первое, получим:
Таким образом, зная времена истечения взятых жидкостей Вискозиметр БПЖ-2 (рис.3.2) представляет собой U-образную трубку, в колено 1 которой впаян капилляр 7. При измерении жидкость из резервуара 4 течет по капилляру 5 в расширение 6. Вискозиметр заполняют следующим образом: жидкость наливают с помощью воронки в широкое колено 2 вискозиметра. Зажимают это колено пальцем и с помощью груши 3 поднимают жидкость в узком колене выше отметки М1. Убирают палец и определяют время опускания мениска жидкости от отметки М1 до отметки М2.
Порядок выполнения работы
1. Прополоскайте тщательно прибор водой из водопроводного крана, а затем небольшим количеством дистиллированной воды. 2. Заполните вискозиметр дистиллированной водой, как это указано выше и определите время истечения воды. 3. Прополоскайте вискозиметр небольшим количеством исследуемой жидкости и, заполнив прибор, определите время ее истечения. 4. Плотность исследуемой жидкости определите с помощью пикнометра, а плотность воды и ее вязкость при температуре опыта определите по таблицам. 5. Рассчитайте искомый коэффициент вязкости при Контрольные вопросы
1. Какие явления переноса вы знаете? В чем они заключаются? 2. Объясните молекулярно-кинетический механизм вязкости жидкости. 3. Как зависит вязкость жидкости от температуры? 4. Сформулируйте закон Ньютона для вязкого трения.. 5. В чем заключается физический смысл коэффициента вязкости? 6. Сформулируйте закон Пуазейля. 7. Выведите формулу (3.3), по которой определяется коэффициент вязкости. ЛАБОРАТОРНАЯ РАБОТА №6
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.116.34 (0.01 с.) |

 В данной работе для определения числа Авогадро используется метод растекания капли. Если капля раствора олеиновой кислоты в легко летучей жидкости падает на поверхность воды, то растворитель быстро испаряется, а олеиновая кислота, растекаясь, образует на поверхности воды мономолекулярную пленку. Если поверхность воды посыпать предварительно легким слоем пробковых опилок или талька, то на ней образуется хорошо наблюдаемое, свободное от порошка круглое пятно.
В данной работе для определения числа Авогадро используется метод растекания капли. Если капля раствора олеиновой кислоты в легко летучей жидкости падает на поверхность воды, то растворитель быстро испаряется, а олеиновая кислота, растекаясь, образует на поверхности воды мономолекулярную пленку. Если поверхность воды посыпать предварительно легким слоем пробковых опилок или талька, то на ней образуется хорошо наблюдаемое, свободное от порошка круглое пятно.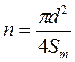 (2.7).
(2.7).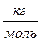 :
: NА ( 2.8),
NА ( 2.8), =
=  NА ( 2.9).
NА ( 2.9). ( 2.10).
( 2.10). и массу олеиновой кислоты в одной капле раствора: m=0,01mр.
и массу олеиновой кислоты в одной капле раствора: m=0,01mр. и времени
и времени 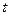 . Поверхности одинаковой температуры, уравнение которых можно представить в виде:
. Поверхности одинаковой температуры, уравнение которых можно представить в виде:  называются изотермическими поверхностями.
называются изотермическими поверхностями. , которое проходит внутри тела через элемент поверхности
, которое проходит внутри тела через элемент поверхности  определяется уравнением Фурье:
определяется уравнением Фурье: ,
, время,
время,  коэффициент теплопроводности,
коэффициент теплопроводности,  – падение (градиент) температуры по направлению
– падение (градиент) температуры по направлению 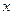 , которое служит нормалью к изотермической поверхности.
, которое служит нормалью к изотермической поверхности.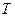 .
. численно равен количеству теплоты, переносимую через единицу поверхности, за единицу времени, при градиенте температуры, равном единице.
численно равен количеству теплоты, переносимую через единицу поверхности, за единицу времени, при градиенте температуры, равном единице.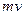 молекулам слоя, движущегося медленнее. Это приводит к увеличению скорости движения более медленного слоя. Слой же, движущейся быстрее, начинает двигаться медленнее, так как молекулы из медленного слоя, попадая в более быстрый слой, получают в быстром слое некоторое количество движения, что приводит к его торможению.
молекулам слоя, движущегося медленнее. Это приводит к увеличению скорости движения более медленного слоя. Слой же, движущейся быстрее, начинает двигаться медленнее, так как молекулы из медленного слоя, попадая в более быстрый слой, получают в быстром слое некоторое количество движения, что приводит к его торможению.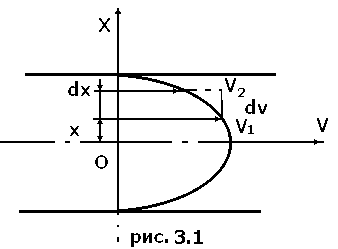 Опыт показал, что сила внутреннего трения
Опыт показал, что сила внутреннего трения  пропорциональна величине площади соприкосновения движущихся слоев
пропорциональна величине площади соприкосновения движущихся слоев  , градиенту скорости
, градиенту скорости 
 движения слоев, коэффициенту пропорциональности h, который называется коэффициентом вязкости (закон Ньютона):
движения слоев, коэффициенту пропорциональности h, который называется коэффициентом вязкости (закон Ньютона): .
.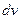 на единицу длины
на единицу длины  в направлении, перпендикулярном скорости движения слоев (рис.3.1). Коэффициент вязкости:
в направлении, перпендикулярном скорости движения слоев (рис.3.1). Коэффициент вязкости: .
. .
.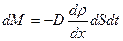 ,
, количество вещества, которое переносится за время
количество вещества, которое переносится за время  через элементарную площадку
через элементарную площадку 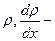 градиент плотности (концентрации), изменение плотности на единицу длины по нормали
градиент плотности (концентрации), изменение плотности на единицу длины по нормали  коэффициент диффузии,
коэффициент диффузии, .
.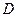 называется физическая величина, численно равная количеству массы вещества, переносимый через единицу площади за единицу времени при градиенте скорости, равном единице в направлении нормали
называется физическая величина, численно равная количеству массы вещества, переносимый через единицу площади за единицу времени при градиенте скорости, равном единице в направлении нормали  (3.1),
(3.1), – длина трубы,
– длина трубы,  – ее радиус,
– ее радиус, 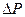 – разность давлений на концах трубы,
– разность давлений на концах трубы, 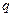 – объем жидкости, протекший через трубу в единицу времени, h – коэффициент вязкости.
– объем жидкости, протекший через трубу в единицу времени, h – коэффициент вязкости. , можно определить коэффициент вязкости h.
, можно определить коэффициент вязкости h.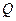 и другой
и другой  ) и измерить времена
) и измерить времена  и
и  истечения одинаковых объемов V этих жидкостей
истечения одинаковых объемов V этих жидкостей  через один и тот же капилляр (одинаковые
через один и тот же капилляр (одинаковые  и
и  .
. , или
, или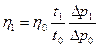 (3.2).
(3.2). Если жидкость вытекает под действием силы тяжести, то
Если жидкость вытекает под действием силы тяжести, то  , где
, где 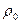 и
и  – плотности жидкостей, и соотношение (3.2) можно написать в виде:
– плотности жидкостей, и соотношение (3.2) можно написать в виде: (3.3).
(3.3). , а найдя из таблиц значения
, а найдя из таблиц значения 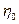 – эталонной жидкости, вычислить и абсолютную величину коэффициента внутреннего трения исследуемой жидкости
– эталонной жидкости, вычислить и абсолютную величину коэффициента внутреннего трения исследуемой жидкости 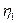 .
. .
. 


