
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение изобарного процессаСодержание книги
Поиск на нашем сайте
Оборудование: прозрачная трубка с двумя кранами на концах, лабораторный термометр, измерительная лента, калориметр, сосуд с теплой водой, сосуд с холодной водой. Цель работы: проверка соотношения между изменением объема и температуры определенного количества газа при его изобарном охлаждении. Содержание и метод выполнения работы
В соответствии с законом Гей-Люссака это соотношение имеет вид:
где Исследуемым газом в данной работе является воздух, находящийся внутри прозрачной трубки. Измерения объема и температуры теплого и холодного воздуха внутри трубки проводят в следующем порядке. Трубку плотно, виток к витку, укладывают внутрь калориметра, предварительно закрыв кран, который расположится вблизи дна. Верхний кран оставляют открытым. В калориметр наливают нагретую до Для перевода воздуха в состояние с другими параметрами закрывают кран, теплую воду сливают и заполняют стакан холодной водой, следя за тем, чтобы ее уровень над верхним краном оказался таким же, как и в первой части опыта. После этого кран опять открывают. При охлаждении объем воздуха уменьшится, и через открытый кран в трубку поступит некоторое количество воды. Когда температура воздуха и воды станут одинаковыми (через 1-2 минуты), приступают к определению параметров газа в новом состоянии. Температуру воздуха вновь определяют по температуре воды. Чтобы определить его объем после охлаждения, закрывают верхний кран, трубку извлекают из калориметра и, удерживая вертикально, резко встряхивают несколько раз. При этом капли воды, попавшие внутрь, сольются и образуют неразрывный столбик. Измерив объем этого водяного столба и вычтя его из внутреннего объема трубки, определяют объем воздуха в конечном состоянии. Объем измеряется, как и в первом упражнении, по длине воздушного или водяного столба. Давление воздуха в трубке в первой и второй части опыта равнялось сумме атмосферного давления и давления небольшого столба воды над открытым краном. Поскольку уровень теплой и холодной воды не менялся, то эта сумма в ходе опыта не менялась, а значит и давление воздуха в трубке при его охлаждении оставалась постоянным, то есть процесс протекал изобарический. В завершении работы сравнивают отношения объема воздуха к его температуре до и после охлаждения.
Порядок выполнения работы
1. Подготовьте таблицу для записи результатов измерений и вычислений:
2. Измерьте длину воздушного столба в трубке – 3. Закройте один кран и уложите трубку виток к витку в стакан калориметра. Кран на верхнем конце оставьте открытым. 4. Заполните стакан теплой водой и поместите в него термометр. 5. Наблюдайте за выделением пузырьков воздуха из открытого крана. Как только оно прекратится, определите показание термометра – 6. Закройте кран, слейте теплую воду, заполните стакан холодной водой до прежнего уровня, и снова откройте кран. 7. Выждав полторы-две минуты, определите температуру – 8. Закройте кран, слейте воду, извлеките трубку из стакана, встряхните его и измерьте длину столба воды в нем 9. Вычислите длину столба охлажденного воздуха: 10. Переведите записанные показания термометра в градусы Кельвина: 11. Вычислите отношения 12. Укажите причины, повлиявшие на точность полученных результатов.
Контрольные вопросы
1. Сформулируйте законы идеального газа. 2. Почему процесс сжатия воздуха в упражнении 1 можно считать изотермическим? 3. Какие условия должны выполняться, чтобы, определяя параметры газа, можно было воспользоваться законом Бойля-Мариотта? 4. Почему процесс охлаждения воздуха в упражнении 2 можно считать изобарным? 5. Какие условия должны выполняться, чтобы, определяя параметры газа, можно было воспользоваться законом Гей-Люссака?
II. ЖИДКОСТИ
Жидкость является агрегатным состоянием вещества, промежуточным между газообразным и твердым, поэтому она обладает свойствами как газообразных, так и твердых веществ. Жидкости, подобно твердым телам, обладают определенным объемом, а подобно газам, принимают форму сосуда, в котором они находятся. Для кристаллического состояния характерно упорядоченное расположение частиц (атомов и молекул), а в газах в этом смысле царит полный хаос. Согласно рентгенографическим исследованиям в отношении характера расположения частиц жидкости также занимают промежуточное положение. В расположении частиц жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от данной частицы расположение по отношению к ней других частиц становится все более и более неупорядоченным, и довольно быстро порядок расположения частиц полностью исчезает. Молекулы жидкости совершают колебания около временных положений равновесия. Побыв некоторое время в таком состоянии, молекула «перескакивает» в другое место и снова какое-то время живет в этом месте «оседлой жизнью». В таком состоянии молекулу жидкости удерживают упругие силы, обусловленные действием соседних молекул, расположенных на близком расстоянии. Молекулярные силы очень быстро убывают с увеличением расстояния. При сближении молекул друг с другом силы взаимного притяжения до определенного расстояния возрастают, при некотором расстоянии между молекулами
Молекулы поверхностного слоя жидкости обладают избытком энергии сравнительно с молекулами, находящимися внутри жидкости. Эта избыточная энергия Указанными свойствами поверхностного слоя обусловлено особое его состояние, которое подобно состоянию натянутой упругой пленки, стремящейся сократить свою поверхность до малых размеров. Это стремление жидкости сократить свою свободную поверхность называется поверхностным натяжением. Силы поверхностного натяжения Для количественной характеристики силы поверхностного натяжения жидкости вводят коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения можно также определить через величину свободной поверхности энергии. Коэффициент поверхностного натяжения численно равен свободной поверхности энергии W, рассчитанной на квадратный метр поверхности жидкости S:
Коэффициент поверхностного натяжения различен для разных жидкостей. Он зависит от рода жидкости, температуры (уменьшается с повышением температуры) и от степени чистоты поверхности.
Рассмотрим явления на границе жидкости и твердого тела. Капля может собираться на поверхности твердого тела (рис.2.3). В этом случае силы взаимодействия между молекулами жидкости больше, чем между молекулами жидкости и твердого тела ( В узких стеклянных трубках, капиллярах, опущенных в жидкость, хорошо заметно поднятие или опускание жидкости (рис.2.4). Поверхностная пленка жидкости в трубке под действием молекулярных сил жидкости и стекла может принимать как вогнутую, так и выпуклую форму (вогнутый или выпуклый мениск). На такой искривленной поверхности силы поверхностного натяжения вызывают добавочное давление
где R1 и R2 –радиусы кривизны поверхности и жидкости. Если поверхность сферическая, то Этим добавочным давлением, т.е. давлением, обусловленным кривизной мениска, вызываются явления поднятия (а в случае несмачивающий жидкости – опускание) жидкости в капиллярах. Жидкость поднимается или опускается в капилляре до тех пор, пока добавочное давление не сравняется с гидростатическим давлением поднявшегося или опустившегося столба жидкости (рис.2.4). Если считать, что жидкость полностью смачивает поверхность трубки, то радиус кривизны мениска Из этого равенства определяем коэффициент поверхностного натяжения: Капиллярные явления играют большую роль в природе и технике. Например, влагообмен в почве и в растениях осуществляется за счет поднятия воды по тончайшим капиллярам. На капиллярном явлении основано действие фитилей, впитывание влаги бетоном и т. д.
ЛАБОРАТОРНАЯ РАБОТА № 3 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ
Существует ряд методов определения коэффициента поверхностного натяжения жидкости. В настоящей работе определение коэффициента поверхностного натяжения проводится тремя методами, которые предлагаются для выполнения как три упражнения.
Вопросы к допуску: 1. Почему поверхностный слой жидкости обладает особыми свойствами? 2. Какая физическая величина называется коэффициентом поверхностного натяжения? 3. Как определяется коэффициент поверхностного натяжения в каждом из упражнений данной лабораторной работы?
Упражнение 1
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.232.9 (0.012 с.) |

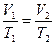 ,
,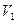 и
и 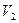 – объемы, занимаемые данной массой газа соответственно до и после охлаждения, а
– объемы, занимаемые данной массой газа соответственно до и после охлаждения, а 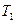 и
и 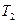 – его температуры.
– его температуры.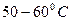 воду. Воду наливают так, чтобы открытый кран оказался погруженным в нее не более чем на
воду. Воду наливают так, чтобы открытый кран оказался погруженным в нее не более чем на 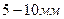 . По мере прогрева объем воздуха в трубке будет возрастать, и из открытого крана станут выходить пузырьки. В момент, когда температура воздуха сравняется с температурой теплой воды, выделение пузырьков прекратится. Это состояние воздуха в трубке принимают за исходное. Температуру воздуха в исходном состоянии
. По мере прогрева объем воздуха в трубке будет возрастать, и из открытого крана станут выходить пузырьки. В момент, когда температура воздуха сравняется с температурой теплой воды, выделение пузырьков прекратится. Это состояние воздуха в трубке принимают за исходное. Температуру воздуха в исходном состоянии 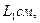

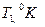
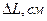
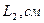
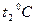
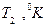
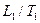
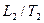
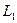 (рис1.6).
(рис1.6).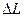 (рис.1.7).
(рис.1.7).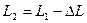 .
.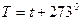 .
. и
и 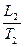 и сделайте вывод о том, насколько точно изменение параметров газа в проделанном опыте соответствует закону Гей-Люссака.
и сделайте вывод о том, насколько точно изменение параметров газа в проделанном опыте соответствует закону Гей-Люссака. силы взаимодействия превращаются в нуль, если же расстояние между молекулами жидкости
силы взаимодействия превращаются в нуль, если же расстояние между молекулами жидкости  , то вступают в действие силы отталкивания. В жидкости молекулы в основном находятся на расстоянии друг от друга меньшем
, то вступают в действие силы отталкивания. В жидкости молекулы в основном находятся на расстоянии друг от друга меньшем  , т. е. в жидкости преобладают силы отталкивания. Этим объясняется слабая сжимаемость жидкостей.
, т. е. в жидкости преобладают силы отталкивания. Этим объясняется слабая сжимаемость жидкостей. Молекулы жидкости, расположенные на поверхности, находятся в особом состоянии, например, молекулы
Молекулы жидкости, расположенные на поверхности, находятся в особом состоянии, например, молекулы  и
и 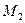 (рис.2.1). Действие на эти молекулы со стороны молекул жидкости больше, чем со стороны молекул воздуха, и поэтому равнодействующая всех действующих на молекулу
(рис.2.1). Действие на эти молекулы со стороны молекул жидкости больше, чем со стороны молекул воздуха, и поэтому равнодействующая всех действующих на молекулу 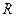 направлена внутрь жидкости нормально к ее поверхности. Отсюда следует, что на все молекулы, расположенные в тонком поверхностном слое, действуют силы, стремящиеся втянуть их внутрь жидкости. Благодаря этому поверхностный слой давит с силой на жидкость, создавая в ней так называемое внутреннее или молекулярное давление.
направлена внутрь жидкости нормально к ее поверхности. Отсюда следует, что на все молекулы, расположенные в тонком поверхностном слое, действуют силы, стремящиеся втянуть их внутрь жидкости. Благодаря этому поверхностный слой давит с силой на жидкость, создавая в ней так называемое внутреннее или молекулярное давление.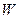 называется свободной поверхностной энергией.
называется свободной поверхностной энергией. направлены по касательной к поверхности жидкости и действуют нормально к любой линии, проведенной на этой поверхности.
направлены по касательной к поверхности жидкости и действуют нормально к любой линии, проведенной на этой поверхности. , который численно равен силе
, который численно равен силе  , мысленно проведенной на поверхности жидкости:
, мысленно проведенной на поверхности жидкости: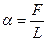 (Н/м).
(Н/м).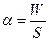 (Дж/м2).
(Дж/м2).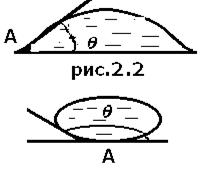 Растворение в жидкости различных веществ изменяет коэффициент поверхностного натяжения. Некоторые из них адсорбируются (повышенная концентрация) на свободной поверхности и уменьшают коэффициент поверхностного натяжения. Такими веществами являются жирные кислоты, их соли, спирты, эфиры, они называются поверхностно-активными веществами.
Растворение в жидкости различных веществ изменяет коэффициент поверхностного натяжения. Некоторые из них адсорбируются (повышенная концентрация) на свободной поверхности и уменьшают коэффициент поверхностного натяжения. Такими веществами являются жирные кислоты, их соли, спирты, эфиры, они называются поверхностно-активными веществами. На поверхности твердого тела форма капли может быть разной. Капля может растекаться по поверхности твердого тела (рис.2.2), это означает, что сила взаимодействия между молекулами жидкости меньше, чем между молекулами жидкости и твердого тела, в этом случае жидкость смачивает поверхность твердого тела. Угол
На поверхности твердого тела форма капли может быть разной. Капля может растекаться по поверхности твердого тела (рис.2.2), это означает, что сила взаимодействия между молекулами жидкости меньше, чем между молекулами жидкости и твердого тела, в этом случае жидкость смачивает поверхность твердого тела. Угол 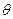 (краевой угол) между плоскостью, касательной к поверхности жидкости в точке А, и поверхностью твердого тела меньше
(краевой угол) между плоскостью, касательной к поверхности жидкости в точке А, и поверхностью твердого тела меньше 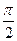 .
.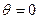 , то наблюдается полное смачивание, а при
, то наблюдается полное смачивание, а при 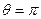 , наблюдается полное несмачивание.
, наблюдается полное несмачивание.
 , обусловленное кривизной поверхности, направленное всегда в сторону вогнутости поверх
, обусловленное кривизной поверхности, направленное всегда в сторону вогнутости поверх  ности. Величина добавочного давления над произвольной поверхностью вычисляется по формуле Лапласа:
ности. Величина добавочного давления над произвольной поверхностью вычисляется по формуле Лапласа: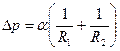 ,
,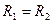 и
и 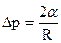 , где
, где  . По равенству добавочного и гидростатического давлений можно написать:
. По равенству добавочного и гидростатического давлений можно написать: 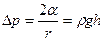 , где
, где 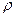 – плотность жидкости,
– плотность жидкости, 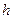 – высота ее поднятия.
– высота ее поднятия.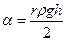 .
.


