
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение величины ошибки при прямых измеренияхСодержание книги
Поиск на нашем сайте
Пусть, измеряя некоторую величину х, мы получим серию результатов х1, х2, х3,..... хn. Которое из этих значений является наиболее близким к истинному? Теория ошибок указывает, что наиболее близким к истинному значению измеряемой величины будет среднее арифметическое значение ряда отдельных измерений, т. е.
Причем, при n®¥, xср®хист. При вычислении среднего арифметического ошибки в сторону увеличения и уменьшения величины наилучшим образом компенсируют друг друга. Величина
называется отклонением данного i - того измерения от среднего. Абсолютная величина наибольшего из этих отклонений определяет границы интервала значений искомой величины. Предположим, при измерении величины x мы получим ряд значений 1,790; 1,795; 1,800; 1,805; 1,810; а пользуясь другим прибором, получим 1,76; 1,78; 1,80; 1,82; 1,84. В обоих случаях среднее значение x = 1,80, но интервалы допустимых значений в первом и во втором случаях не одинаковы и равны соответственно (1,79 Если повторять измерение большое число раз, то внутри интервала, ограниченного наибольшими отклонениями, будет располагаться все большее число полученных значений. Если весь интервал разброса разбить на равные участки dх, то большее количество результатов в них будет помещаться на центральных участках, а по мере удаления от центра число результатов, приходящихся на участок dх, будет убывать. Обозначим относительное число всех измерений, приходящихся на участок dх, через Если мы вычертим график зависимости
Из рисунка 1 видно, что чем больше участок dх удален от хср, тем меньше результатов измерения на него приходится. Не вникая в детали статистической теории погрешности, скажем лишь, что при
где
при Если мы провели не одну, а несколько серий (m - серий) измерений и в каждой получили среднеарифметическое значение хср.к(где к - номер серии), то эти значения также распределились вокруг искомого хист, но уже с меньшим разбросом, который характеризовался бы среднеквадратичной ошибкой среднего
отсюда, считая S хорошим приближением для
На практике удобнее определять
где Истинное значение измеряемой величины принципиально недостижимо, за исключением редких случаев. Величина
хср- σ m хср хср+ σ m
2 σ m
Рис.2 Однако все эти рассуждения справедливы лишь в случае точно заданной величины Dх = tan sm, будет определяться коэффициентом tan, зависящим как от числа проведенных измерений (n), так и заданной доверительной вероятностью ( Так, для n = 5 и Значение коэффициентов Стьюдента приводится в таблице 1.
Таблица №1 Коэффициенты Стьюдента
Относительная ошибка
Абсолютная погрешность измерения не характеризует полностью точности проведенных измерений. Действительно, если мы измерили массу с точностью ε - безразмерная величина, определяемая в процентах.
4. Пример записи результатов прямых измерений В лаборатории при измерении любой величины результаты должны заноситься в таблицу, которую необходимо составить заранее. Например: необходимо измерить диаметр цилиндра. Для записи результатов измерений составим таблицу:
Далее определим среднюю квадратичную ошибку среднего арифметического, пользуясь формулой Питерса:
выберем доверительную вероятность результата Запишем результат:
Обычно результат округляют до сомнительной цифры. Сомнительной является цифра, разряд которой совпадает с разрядом старшей, отличной от 0, цифры ошибки. В данном результате это цифра 2. Причем, при округлении последняя цифра остается без изменения, если старшая отбрасываемая цифра меньше 5; увеличивается на 1, если эта цифра больше 5. Если отбрасываемая цифра 5, то последняя сохраняется, если она четная, и увеличивается на единицу, если она нечетная. Исключение: при округлении ошибок (погрешностей) последняя сохраняемая цифра всегда увеличивается на единицу, если только старшая отбрасываемая цифра не нуль. Ошибки обычно округляются до одной значащей цифры. В некоторых случаях, когда первая значащая цифра меньше или равна 3, оставляются две значащие цифры. Это связано с тем, что сами погрешности определяются с погрешностью, например, при 10 измерениях эта погрешность составляет величину 30%. Таким образом, результат измерения диаметра после округления запишется: d = Если проведенная серия измерений дала одинаковые результаты, то это означает, что величина случайных отклонений меньше точности прибора. В этом случае за ошибку принимают величину, обусловленную классом точности прибора или половиной цены его наименьшего деления, а в случае, если случайная ошибка и погрешность измерительного прибора сравнимы, то общая ошибка складывается из них. Правила сложения даны ниже. Суммарная погрешность определяется согласно формуле:
где Dхсл – случайная ошибка, d - погрешность измерительного прибора.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.146.94 (0.01 с.) |

 .
.
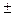 1,81) и (1,76
1,81) и (1,76  , где n - общее число всех измерений. Тогда на единичный отрезок интервала придется относительное число значений
, где n - общее число всех измерений. Тогда на единичный отрезок интервала придется относительное число значений  .
. от х, то получим кривую, показанную на рис. 1.
от х, то получим кривую, показанную на рис. 1.
 вид кривой, приведенной на рис. I, хорошо описывается функцией Гаусса
вид кривой, приведенной на рис. I, хорошо описывается функцией Гаусса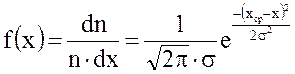 ,
,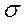 - так называемое среднеквадратичное отклонение, определяющее ширину интервала разброса результатов измерения. Величина
- так называемое среднеквадратичное отклонение, определяющее ширину интервала разброса результатов измерения. Величина  стремится к нулю по обе стороны от хср. Приближенно можно считать, что полуширина кривой Гаусса на ее полувысоте равняется
стремится к нулю по обе стороны от хср. Приближенно можно считать, что полуширина кривой Гаусса на ее полувысоте равняется 
 .
. .
. 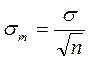 ,
, или
или  .
.
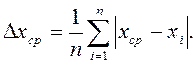
 (коэффициента надежности), а сам интервал хср ± sm – называется доверительным интервалом. Величина a возрастает от 95% или 0,95 внутри интервала хср ± 2sm и до 99,7% или 0,997 внутри интервала хср ± 3sm.
(коэффициента надежности), а сам интервал хср ± sm – называется доверительным интервалом. Величина a возрастает от 95% или 0,95 внутри интервала хср ± 2sm и до 99,7% или 0,997 внутри интервала хср ± 3sm. х
х = 2,8, а ширина доверительного интервала
= 2,8, а ширина доверительного интервала  . Эта величина и должна приводиться в качестве ошибки.
. Эта величина и должна приводиться в качестве ошибки.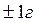 , то точность измерений в значительной мере будет зависеть от того, какую величину мы измерили: 2 кг или 2 г. Поэтому для того, чтобы иметь возможность сравнивать точность различных измерений величин разной размерности, принято находить среднюю относительную погрешность результата, которая определяется отношением абсолютной ошибки к среднему арифметическому значению измеряемой величины:
, то точность измерений в значительной мере будет зависеть от того, какую величину мы измерили: 2 кг или 2 г. Поэтому для того, чтобы иметь возможность сравнивать точность различных измерений величин разной размерности, принято находить среднюю относительную погрешность результата, которая определяется отношением абсолютной ошибки к среднему арифметическому значению измеряемой величины: 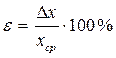 .
.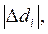 мм
мм
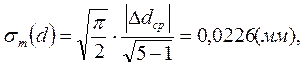
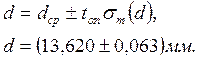
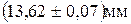 .
. ,
,


