
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и основные законы динамикиСодержание книги
Поиск на нашем сайте
I Динамика точки Вопрос Предмет и основные законы динамики В динамике изучаются механические движения материальных объектов под действием сил. Простейшим материальным объектом является материальная точка. Материальная точка это модель материального тела любой формы, размерами которого можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты – механические системы и твердые тела, состоят из набора материальных точек. Движение материальных объектов всегда происходит в пространстве относительно определенной системы отсчета и во времени. Пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково. В динамике изучаются механические движения материальных объектов под действием сил. Простейшим материальным объектом является материальная точка. Материальная точка это модель материального тела любой формы, размерами которого можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты – механические системы и твердые тела, состоят из набора материальных точек. Движение материальных объектов всегда происходит в пространстве относительно определенной системы отсчета и во времени. Пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково.
Аксиомы классической механики Первая аксиома или закон инерции. Материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способностью сохранять свое состояние покоя или равномерного и прямолинейного движения относительно инерциальной системы отсчета. Материальная точка, на которую действует равновесная система сил, называется изолированной материальной точкой. Равномерное и прямолинейное движение точки называется движением по инерции. Вторая аксиома или основной закон динамики. Ускорение материальной точки относительно инерционной системы отсчета пропорционально приложенной к точке силе и направлено по этой силе.
Положительный коэффициент пропорциональности m, характеризует инертные свойства материальной точки и называется массой точки.
Рис. 1-1 Масса не зависит от характеристик движения точки и от природы сил. Масса считается постоянной величиной и зависит только от самой материальной точки. Сила, приложенная к материальной точке, всегда имеет материальный источник в виде других материальных тел, которые действуют на точку путем контакта при непосредственном соприкосновении с ней или на расстоянии через посредство силовых полей.
Рис. 1-2
Четвертая аксиома или закон независимого действия сил. При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.
Вопрос Вопрос Дифференциальные уравнения движения несвободной материальной точки Вопрос Две основные задачи динамики(1 и 2 задача динамики) Основные задачи динамики Первая или прямая задача: Известна масса точки и закон ее движения, необходимо найти действующую на точку силу. m Вычисляем вторые производные по времени от координат точки, умножаем их на массу и получаем проекции силы на оси координат
Зная проекции силы на оси координат, определяем модуль силы и ее направляющие косинусы:
Вторая или обратная задача: Известна масса точки и действующая на точку сила, необходимо определить закон движение этой точки. Рассмотрим решение этой задачи в декартовой системе координат. Сила зависит от времени, координат точки, ее скорости и других причин.
Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных: Каждая из координат
К этим уравнениям необходимо добавить начальные условия:
Используя эти начальные условия можно получить шесть алгебраических уравнений для определения шести произвольных постоянных
Вопрос Вопрос Наиболее важные случаи. 1. Сила постоянна. Имеем равнопеременное движение (движение с постоянным ускорением) 2. Сила зависит от времени.
3. Сила зависит от координаты или скорости. Силу, зависящую от координаты х Сила, зависящая от скорости движения В этих случаях решение задачи упрощается.
Вопрос движение точки брошенной под углом к горизонту(траектория,дальность,высота полета) Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
где Координаты тела, следовательно, изменяются так:
При нашем выборе начала координат начальные координаты
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл. Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение (2) в первую формулу (1), получаем:
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов. Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
и подставить его во второе уравнение. Тогда получим:
Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
Вопрос Количество движения точки
Количеством движения материальной точки Количество движения точки в физике часто называют импульсом материальной точки. Проекции количества движения точки на прямоугольные декартовы оси координат равны:
Единицей измерения количества движения в СИ является –
Вопрос
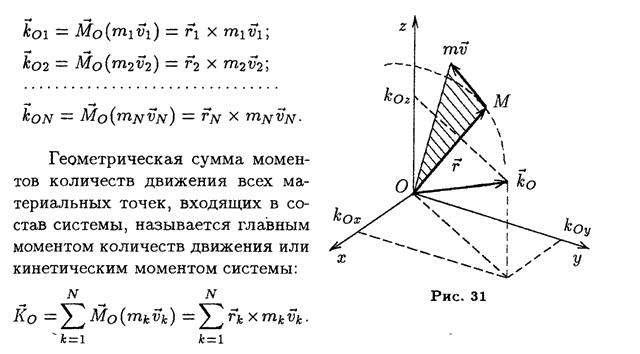
Вопрос Вопрос Момент количества движения Момент количества движения точки М относительно центра О − это вектор, направленный перпендикулярно плоскости, проходящей через вектор количества движения и центр О в ту сторону, откуда поворот вектора количества движения относительно центра О виден против движения часовой стрелки. Момент количества движения точки М относительно ос и равен произведению проекции вектора количества движения на плоскость перпендикулярную к оси на плечо этой проекции относительно точки О пересечения оси с плоскостью. Вопрос Вопрос Вопрос Работа силы упругости.
Работа силы упругости равна половине произведения жесткости упругого элемента на разность квадратов начального и конечного удлинения (или сжатия) упругого элемента. Работа силы упругости равна площади фигуры (трапеции) расположенной под кривой
Вопрос Вопрос Вопрос IV Динамика системы Вопрос Вопрос Моменты инерции. основные понятия и определения Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции. Момент инерции относительно точки Скалярная величина
называется полярным моментом инерции относительно точки О. d – расстояние от текущей точки до точки О. Момент инерции относительно оси Скалярная величина называется моментом инерции относительно оси l. r – расстояние от точки до оси. Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Величина Момент инерции относительно оси через радиус инерции относительно этой же оси определяется выражением Моменты инерции относительно осей координат
Центробежные моменты инерции
Установим зависимость между моментами инерции относительно параллельных осей, одна из которых проходит через центр масс.
Вопрос Теорема о моментах инерции относительно параллельных осей. (Теорема Штейнера)
Момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями. Доказательство: Пусть имеется две декартовы системы координат
Координаты связаны между собой соотношениями:
Следовательно
Главными осями инерции называются оси, в которых центробежные моменты инерции равны нулю. Моменты инерции тела относительно главных осей инерции называются главными моментами инерции тела.
Тензор инерции и тензор инерции для главных осей:
Вопрос Рис.7
По определению момент инерции Поместим в точку О начало координатных осей x, y, z. Из прямоугольного треугольника ОАМi следует
Как известно из тригонометрии Поэтому
И, группируя подобные члены, содержащие косинусы одинаковых углов, получим:
Но где Поэтому
где Ix, Iy, Iz – моменты инерции тела относительно осей координат; Ixy, Jyz, Jxz - центробежные моменты инерции относительно осей отмеченных в индексах. Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется главной осью инерции. Например, если Jyz = 0 и Jxz = 0, то ось z – главная ось инерции. Так как все моменты инерции зависят от того, где находится точка О, от выбора начала координат, то обязательно надо указать для какой точки определены эти моменты инерции. Если начало координат взято в центре масс С, то все главные оси инерции называются главными центральными осями инерции. Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (2) упрощается:
Иногда по некоторым признакам нетрудно найти главные оси инерции тела. 1. Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции. Действительно. Направим координатную ось z по оси симметрии. Тогда для каждой точки тела с координатами (xi, yi, zi) можно отыскать точку с координатами (-xi, -yi, -zi) и поэтому центробежные моменты инерции 2. Если у однородного тела имеется плоскость симметрии, то любая ось перпендикулярная ей будет главной осью инерции для всех точек этой плоскости. Направим ось z перпендикулярно плоскости симметрии из любой её точки О, назначив там начало координат. Тогда для каждой точки тела с координатами (xi, yi, zi) можно найти симметричную ей точку с координатами (xi, yi, - zi). Поэтому центробежные моменты инерции Ixz и Iyz будут равны нулю. Значит ось z – главная ось инерции.
Вопрос Вопрос Вопрос Свойства внутренних сил Внутренними силами механической системы называются силы взаимодействия между точками и телами рассматриваемой системы. Равнодействующая всех внутренних сил приложенных к Это разделение является условным и зависит от того, какая механическая система рассматривается. Внутренние силы системы обладают следующими свойствами: Теорема. Главный вектор всех внутренних сил системы (векторная сумма) равен нулю при любом состоянии системы. Доказательство: Согласно одной из аксиом динамики, любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Векторная сумма этих сил равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма всех внутренних сил равна нулю.
Теорема. Главный момент всех внутренних сил системы (векторная сумма) относительно любой точки или оси равен нулю при любом состоянии системы. Доказательство: Любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Сумма моментов этих сил относительно любой точки или оси равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма моментов всех внутренних сил относительно любой точки или оси равна нулю.
Дифференциальные уравнения системы в векторной форме:
Вопрос Вопрос Вопрос Вопрос Вопрос Вопрос Закон о сохранении движения центра масс системы:
Вопрос Кинетический момент системы Кинетический момент системы равен векторной сумме момента количества движения материальной точки, находящейся в центре инерции системы и имеющей массу, равную массе системы, относительно центра О, и кинетического момента движения системы относительно ее центра инерции
Вопрос Вопрос Вопрос Вопрос Вопрос Вопрос Работа силы тяжести.
Тогда,
Работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.
Вопрос Вопрос Вопрос Вопрос Вопрос Потенциальная энергия Потенциальная энергия это энергия взаимодействия тел, либо частей тела, между собой. В потенциальном поле консервативных сил. Она зависит от расстояния, на котором находятся тела, и не зависит от их скорости. Таким образом, потенциальная энергия это скалярная величина, имеющая числовое значение, но не имеющая вектора направления. Также она способна совершать работу под действием сил поля.
Примером потенциальной энергии можно считать, такую энергию которой обладает тело массой m подвешенное на некотором расстоянии от земли. В данном случае взаимодействуют два тела. Это земля и подвешенный груз. Роль потенциального поля сил играет гравитационное поле земли. Консервативная сила в данном случае это сила тяжести. Расстоянием между телами считается расстояние между грузом и поверхностью земли.
Вопрос Вопрос Вопрос Вопрос Связи. классификация связей Связь называется удерживающие (налагаемые или ограничения сохраняются при любом положении системы) и неудерживающие, которые этим свойством не обладают (от таких связей, как говорят, система может “освобождаться” Классификация: Геометрические – накладывает ограничения только на координаты точек системы (скорости не входят) Кинематические – скорости входят в уравнения. Если от скоростей можно избавиться, то связь интегрируемая. Голономные связи – геометрические и интегрируемые дифференциальные связи. Неголономными называются связи, которые описываются уравнениями вида:
Вопрос Вопрос Вопрос
Вопрос
Вопрос Общее уравнение динамики
I Динамика точки Вопрос предмет и основные законы динамики В динамике изучаются механические движения материальных объектов под действием сил. Простейшим материальным объектом является материальная точка. Материальная точка это модель материального тела любой формы, размерами которого можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты – механические системы и твердые тела, состоят из набора материальных точек. Движение материальных объектов всегда происходит в пространстве относительно определенной системы отсчета и во времени. Пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково. В динамике изучаются механические движения материальных объектов под действием сил. Простейшим материальным объектом является материальная точка. Материальная точка это модель материального тела любой формы, размерами которого можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты – механические системы и твердые тела, состоят из набора материальных точек. Движение материальных объектов всегда происходит в пространстве относительно определенной системы отсчета и во времени. Пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.126.241 (0.009 с.) |



 Третья аксиома или закон о равенстве сил действия и противодействия. Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению.
Третья аксиома или закон о равенстве сил действия и противодействия. Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению. 










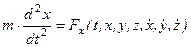 ,
,  ,
,

 движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е.
движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е.


 ,
, 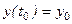

 ,
, 

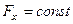

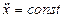




 , создают упругие тела при их деформации (например, сжатая или растянутая пружина).
, создают упругие тела при их деформации (например, сжатая или растянутая пружина).  , это сила сопротивления (воздуха, воды и т.д.)
, это сила сопротивления (воздуха, воды и т.д.) ; проекции ускорения на координатные оси равны ах = 0, ау = -g.
; проекции ускорения на координатные оси равны ах = 0, ау = -g.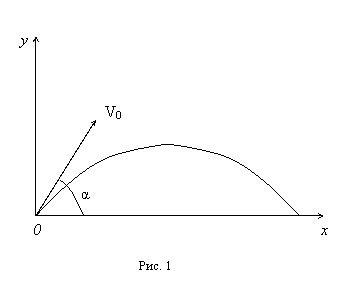 Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1). ,
, – начальная скорость, α – угол бросания.
– начальная скорость, α – угол бросания.
 (рис. 1) Тогда
(рис. 1) Тогда
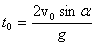 .
.
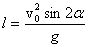 .
.
 .
.

 .
. называется вектор, равный произведению массы точки
называется вектор, равный произведению массы точки 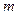 на ее скорость
на ее скорость  .
. 
 ,
,  ,
, 
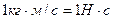

 Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила)
Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила)  . Пусть точка М, на которую действует только сила упругости, перемещается из положения
. Пусть точка М, на которую действует только сила упругости, перемещается из положения  в положение
в положение  . (
. ( ,
,  ).
).

 .
. 
 или
или 
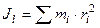 или
или 
 называется радиусом инерции.
называется радиусом инерции. .
.








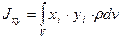





 и
и  , оси которых параллельны. Начало системы
, оси которых параллельны. Начало системы  и
и  .
.


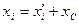 ,
,  ,
, 

 ,
,  ,
,  .
.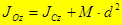 , что и требовалось доказать.
, что и требовалось доказать.

 .
. , где
, где  . И так как радиус-вектор точки
. И так как радиус-вектор точки  :
:  , то, проектируя это равенство на ось u, получим
, то, проектируя это равенство на ось u, получим  (
( ,
,  ,
,  - углы между осью u и осями x, y, z).
- углы между осью u и осями x, y, z). .
.





 - расстояния от точки М i до осей x, y, z, соответственно.
- расстояния от точки М i до осей x, y, z, соответственно.



 . (3)
. (3) и
и 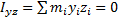 . Значит ось z – главная ось инерции, и центральная ось, т.к. центр масс, как известно, находится на оси симметрии. Причём, эта ось будет главной для любой точки расположенной на оси симметрии.
. Значит ось z – главная ось инерции, и центральная ось, т.к. центр масс, как известно, находится на оси симметрии. Причём, эта ось будет главной для любой точки расположенной на оси симметрии. точке обозначается
точке обозначается 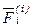 (от латинского interior - внутренний).
(от латинского interior - внутренний). .
. или
или  .
. ,
, 

 Пусть точка М, на которую действует сила тяжести Р, перемещается из положения
Пусть точка М, на которую действует сила тяжести Р, перемещается из положения  в положение
в положение  . Выберем оси координат так, чтобы ось
. Выберем оси координат так, чтобы ось  была направлена вертикально вверх.
была направлена вертикально вверх. ,
,  ,
,  и
и









