
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механическая система. классификация сил действующих на механическую системуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 Механической системой называется любая система материальных точек и тел. Внешними силами механической системы называются силы, с которыми на точки и тела механической системы действуют точки и тела не входящие в рассматриваемую систему. Равнодействующая всех внешних сил приложенных к Внутренними силами механической системы называются силы взаимодействия между точками и телами рассматриваемой системы. Равнодействующая всех внутренних сил приложенных к Это разделение является условным и зависит от того, какая механическая система рассматривается.
Вопрос Свойства внутренних сил Внутренними силами механической системы называются силы взаимодействия между точками и телами рассматриваемой системы. Равнодействующая всех внутренних сил приложенных к Это разделение является условным и зависит от того, какая механическая система рассматривается. Внутренние силы системы обладают следующими свойствами: Теорема. Главный вектор всех внутренних сил системы (векторная сумма) равен нулю при любом состоянии системы. Доказательство: Согласно одной из аксиом динамики, любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Векторная сумма этих сил равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма всех внутренних сил равна нулю.
Теорема. Главный момент всех внутренних сил системы (векторная сумма) относительно любой точки или оси равен нулю при любом состоянии системы. Доказательство: Любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Сумма моментов этих сил относительно любой точки или оси равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма моментов всех внутренних сил относительно любой точки или оси равна нулю.
Дифференциальные уравнения системы в векторной форме:
Вопрос Дифференциальное уравнение движения системы материальных точек
Вопрос Количество движения системы.
Количеством движения системы материальных точек
Единицей измерения количества движения в СИ является – Количество движения системы можно выразить через массу системы и скорость центра масс. Вопрос Теорема об изменении количества движения для системы.
Эта теорема существует в трех различных формах. Теорема. Производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему.
Доказательство: Теорема об изменении количества движения для
Сложим все
что и требовалось доказать. В проекциях на оси координат это утверждение выглядит так:
Теорема. (в дифференциальной форме). Дифференциал от количества движения системы равен сумме элементарных импульсов всех внешних сил, действующих на систему. Умножим левую и правую части уравнения (6.1) на
В проекциях на оси координат это утверждение выглядит так:
Теорема (в интегральной форме). Изменение количества движения системы за какой-либо промежуток времени равно векторной сумме элементарных импульсов всех внешних сил, действующих на систему за этот же промежуток времени. Интегрируя обе части уравнения (**) по времени в пределах от нуля до
В проекциях на оси координат это утверждение выглядит так:
Вопрос Законы сохранения количества движения системы
1. Если главный вектор всех внешних сил системы равен нулю ( 2. Если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю (
Вопрос
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.191.241 (0.007 с.) |

 точке обозначается
точке обозначается  (от латинского exterior - внешний).
(от латинского exterior - внешний).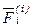 (от латинского interior - внутренний).
(от латинского interior - внутренний). .
. или
или  .
. ,
, 

 называется векторная сумма количеств движений отдельных точек системы.
называется векторная сумма количеств движений отдельных точек системы.
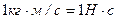

 , (6.1)
, (6.1)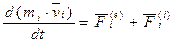 ,
, 
 уравнений и получим:
уравнений и получим: ,
, ,
,  ,
, 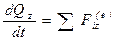 .
.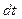 и получим
и получим , (6.2)
, (6.2) ,
,  ,
,  .
. получаем:
получаем:
 ,
,  ,
, 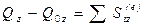 .
. ), то количество движения системы постоянно по величине и направлению.
), то количество движения системы постоянно по величине и направлению. 
 ), то проекция количества движения системы на эту ось является постоянной величиной.
), то проекция количества движения системы на эту ось является постоянной величиной. 



