
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа постоянной силы .Элементарная работа.Полная работа.МощностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.
Единицей измерения работы в СИ является – При Частные случаи:
Элементарное перемещение равно дифференциалу радиуса вектора точки приложения силы. Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.
Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки.
Если сила
Работа силы на любом конечном перемещении
Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.
Мощность равна скалярному произведению силы на скорость. Единицей измерения мощности в СИ является – В технике за единицу силы принимается
Вопрос Работа силы упругости.
Работа силы упругости равна половине произведения жесткости упругого элемента на разность квадратов начального и конечного удлинения (или сжатия) упругого элемента. Работа силы упругости равна площади фигуры (трапеции) расположенной под кривой
Вопрос Теорема об изменении кинетической энергии материальной точки Кинетической энергией материальной точки (или ее живой силой) называют половину произведения массы точки на квадрат ее скорости.
Теорема об изменении кинетической энергии точки. Теорема. Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
Доказательство: Основной закон динамики Умножим левую и правую части уравнения скалярно на
Теорема. Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.
Теорема. Изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на этом же перемещении.
III динамика относительного движения точки Вопрос Дифференциальные уравнения Относительное движение точки Во многих задачах динамики движение материальной точки рассматривается относительно системы отсчета, движущейся относительно инерциальной системы отсчета.
где Согласно теореме Кориолиса Перепишем дифференциальное уравнение следующим образом
Введем обозначения
С учетом этих обозначений мы получаем динамическую теорему Кориолиса (уравнения относительного движения). Материальная точка движется относительно неинерциальной системы отсчета так же как и относительно инерциальной, только к приложенным активным силам и силам реакции связей следует добавить кориолисову и переносную силу инерции.
Силы В проекциях на подвижные оси
Вопрос
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.128.212 (0.008 с.) |

 Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.
Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение. .
.  ,
,

 при
при 





 задана своими проекциями (
задана своими проекциями ( ) на оси координат и элементарное перемещение задано своими проекциями (
) на оси координат и элементарное перемещение задано своими проекциями ( ) на оси координат, то элементарная работа силы равна:
) на оси координат, то элементарная работа силы равна: (аналитическое выражение элементарной работы).
(аналитическое выражение элементарной работы). равна взятому вдоль этого перемещения интегралу от элементарной работы.
равна взятому вдоль этого перемещения интегралу от элементарной работы.
 ,
, 

 .
. Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила)
Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила)  . Пусть точка М, на которую действует только сила упругости, перемещается из положения
. Пусть точка М, на которую действует только сила упругости, перемещается из положения  в положение
в положение  . (
. ( ,
,  ).
).

 .
. 


 .
. справа, получаем
справа, получаем  .
.  - элементарная работа.
- элементарная работа. - дифференциал от кинетической энергии.
- дифференциал от кинетической энергии.


 - инерциальная система отсчета.
- инерциальная система отсчета. - подвижная система отсчета.
- подвижная система отсчета. ,
, - сумма активных сил,
- сумма активных сил, 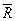 - сумма сил реакции связи.
- сумма сил реакции связи.

 - переносная сила инерции,
- переносная сила инерции, - кориолисова сила инерции.
- кориолисова сила инерции.
 и
и  являются поправками на неинерционность системы.
являются поправками на неинерционность системы.





