
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о движении центра масс системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.
Выводы: 1. Механическую систему или твердое тело можно рассматривать как материальную точку в зависимости от характера ее движения, а не от ее размеров. 2. Внутренние силы не учитываются теоремой о движении центра масс. 3. Теорема о движении центра масс не характеризует вращательное движение механической системы, а только поступательное
Вопрос Закон о сохранении движения центра масс системы:
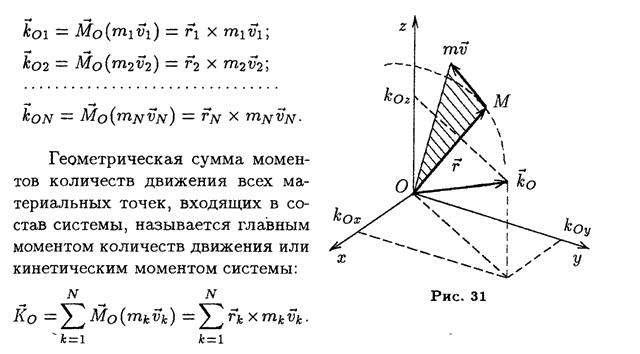
Вопрос Кинетический момент системы Кинетический момент системы равен векторной сумме момента количества движения материальной точки, находящейся в центре инерции системы и имеющей массу, равную массе системы, относительно центра О, и кинетического момента движения системы относительно ее центра инерции
Вопрос Кинематический момент твердого тела, вращающегося вокруг неподвижной оси
Вопрос Теорема об изменении момента количества движения системы.
Теорема. Производная по времени от момента количества движения системы, взятого относительно какого-нибудь центра, равна векторной сумме моментов внешних сил, действующих на систему относительно того же центра.
Доказательство: Теорема об изменении момента количества движения для
Сложим все
что и требовалось доказать. Теорема. Производная по времени от момента количества движения системы, взятого относительно какой-либо оси, равна векторной сумме моментов внешних сил, действующих на систему относительно той же оси. Для доказательства достаточно спроектировать векторное уравнение (6.3) на эту ось. Для оси
Теорема об изменении момента количества движения системы относительно центра масс. (без доказательства) Для осей движущихся поступательно вместе с центром масс системы, теорема об изменении момента количества движения системы относительно центра масс сохраняет тот же вид, что и относительно неподвижного центра.
Вопрос Законы сохранения кинематического момента системы
Вопрос Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Дифференциальное уравнение имеет вид:
Интегрируя уравнение, можно определить закон вращения тела. Методика решения подобных задач: – изображаем тело в произвольном положении; показываем внешние силы, действующие на тело; показываем ось – находим сумму моментов внешних сил относительно оси – вычисляем, если не задан, момент инерции тела – составляем уравнение (2.6), интегрируя это уравнение, определяем закон вращения тела. Вопрос Теорема об изменении кинетической энергии системы
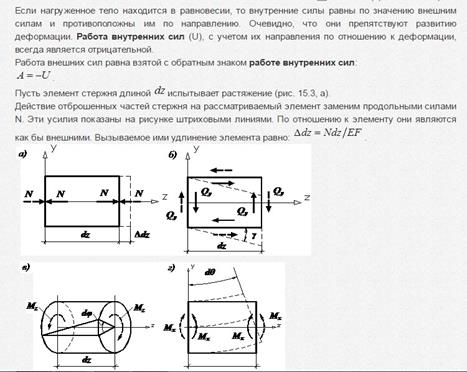
Вопрос Работа внутренних сил. работа силы тяжести
Работа силы тяжести.
Тогда,
Работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.
Вопрос Работа сил вращательного момента
Вопрос Работа сил трения действующих на катящееся тело
Вопрос
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.23.220 (0.01 с.) |


 , следовательно
, следовательно 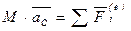



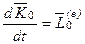 (6.3)
(6.3) точки имеет вид:
точки имеет вид: ,
, 
 уравнений и получим:
уравнений и получим: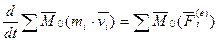 или
или  это будет выглядеть так:.
это будет выглядеть так:. (6.4)
(6.4)
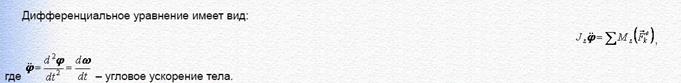
 , направленную по оси вращения тела в ту сторону, откуда вращение видно происходящим против часовой стрелки;
, направленную по оси вращения тела в ту сторону, откуда вращение видно происходящим против часовой стрелки; ;
;

 Пусть точка М, на которую действует сила тяжести Р, перемещается из положения
Пусть точка М, на которую действует сила тяжести Р, перемещается из положения  в положение
в положение  . Выберем оси координат так, чтобы ось
. Выберем оси координат так, чтобы ось  была направлена вертикально вверх.
была направлена вертикально вверх. ,
,  ,
,  и
и






