
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика изучает движение тел, не интересуясь причинами, обусловливающими это движение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кинематика материальной точки. Основные понятия. Характеристики движения: вектор перемещения, путь скорость ускорение. В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.Закон сохранения импульса — Векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия
Докажем закон сохранения импульса. Возьмем и обозначим массы двух тел По третьему закон Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить
Для изменений импульсов тел при их взаимодействии на основании Импульса силы можно записать так Для первого тела:
Для второго тела:
И тогда у нас получается, что закон сохранения импульсов выглядит так:
Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, или равны нулю, сумма импульсов тел остается неизменной. Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета.Систе́маце́нтра масс (систе́маце́нтраине́рции) — невращающаяся система отсчёта, связанная с центром масс механической системы. Обычно сокращается как с. ц. м. или с. ц. и. Суммарный импульс системы вс.ц.м. равен нулю. Для замкнутой системы её система центра масс инерциальна, тогда как незамкнутая система в общем случае может обладать неинерциальной системой центра масс. Суммарная кинетическая энергия механической системы в с.ц.м. минимальна среди всех систем отсчёта; в любой другой невращающейся (необязательно инерциальной) системе отсчёта кинетическая энергия равна кинетической энергии в с.ц.м. плюс кинетическая энергия движения механической системы как целого (MV²/2, где М — полная масса механической системы, V — относительная скорость движения систем отсчёта). При рассмотрении задач рассеяния частиц термин «система центра масс» употребляется как антоним термина «лабораторная система отсчёта». Если экспериментальные исследования проводятся в лабораторной системе, то есть в системе, связанной с наблюдателем (неподвижным относительно частицы-мишени), то теоретическое рассмотрение задач рассеяния удобно проводить в движущейся относительно мишени системе центра масс. При переходе от лабораторной системы в систему центра масс меняются определения углов рассеяния частиц, так что для сравнения теории с экспериментом необходимо проводить перерасчёт полученных сечений рассеяния. Например, при изучении столкновения двух одинаковых частиц, одна из частиц (мишень) до столкновения остается неподвижной, вторая налетает с некоторой конечной скоростью. При упругом лобовом столкновении вторая частица останавливается, передавая всю свою кинетическую энергию и импульс первой частице. Такая картина наблюдается в лабораторной системе отсчета. С точки зрения системы центра масс, частицы движутся навстречу друг другу с одинаковыми скоростями и после столкновения разлетаются в обе стороны с теми же (с точностью до знака) скоростями. В нерелятивистском пределе координаты центра масс системы из n частиц, имеющих массы
(М — масса всей системы тел). Продифференцировав по времени, получим скорость движения центра масс
(
В релятивистском случае центр масс не является лоренц-инвариантом, однако система центра масс определяется и играет важную роль в релятивистской кинематике. Систему центра масс в релятивистском случае следует определять как систему отсчёта, в которой сумма импульсов всех тел системы равна нулю. Потенциальная энергия.Примеры для силовых полей разной природы. Потенциальная кривая. Потенциальная энергия — это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.– потенциальная энергия тела, – его масса, – ускорение свободного падения, – высота тела над некоторым нулевым уровнем. Условное обозначение — Единица измерения энергии — Дж (джоуль).
Потенциальная энергия характеризует энергию тела в некотором поле тяготения. Это скалярная физическая величина. Чаще всего рассматривается поле тяготения, связанное с землёй, в нём 9.8 м.с.Потенциальная кривая – это кривая, выражающая зависимость потенциальной энергии от координаты.Потенциальные кривые позволяют качественно описать характер движения тела. Приведем примеры потенциальных кривых: Определение Преобразование Лоренца (лоренцево преобразование) псевдоевклидова векторного пространства
где треугольными скобками обозначено индефинитное скалярное произведение Аналогично, преобразование Лоренца (лоренцево преобразование) псевдоевклидова аффинного пространства — это аффинное преобразование, сохраняющее расстояние между точками этого пространства (это расстояние определяется как длина вектора, соединяющего данные точки, с помощью индефинитного скалярного произведения).Относительность одновременности событий В механике Ньютона одновременность двух событий абсолютна и не зависит от системы отсчёта. Это значит, что если два события происходят в системе K в моменты времени t и t1, а в системе K’соответственно в моменты времени t’и t’1, то поскольку t=t’, промежуток времени между двумя событиями одинаков в обеих системах отсчёта В отличие от классической механики, в специальной теории относительности одновременность двух событий, происходящих в разных точках пространства, относительна: события, одновременные в одной инерциальной системе отсчёта, не одновременны в других инерциальных системах2, движущихся относительно первой. На рисунке (см. ниже) расположена схема эксперимента, который это иллюстрирует. Система отсчета K связана с Землёй, система K’—с вагоном, движущимся относительно Земли прямолинейно и равномерно со скоростью v. На Земле и в вагоне отмечены точки А, М, В и соответственно А’, M’и В’, причем АМ=МВ и А’M’=M’B’. В момент, когда указанные точки совпадают, в точках А и В происходят события —ударяют две молнии. В системе К сигналы от обоих вспышек придут в точку М одновременно, так как АМ=МВ, и скорость света одинакова во всех направлениях. В системе К’, связанной с вагоном, сигнал из точки В’придет в точку M’раньше, чем из точки А’, ибо скорость света одинакова во всех направлениях, но М’ движется навстречу сигналу пущенному из точки B’ и удаляется от сигнала, пущенного из точки А’. Значит, события в точкахА’иB’не одновременны: события в точке B’произошло раньше, чем в точке A’. Если бы вагон двигался в обратном направлении, то получился бы обратный результат. Понятие одновременности пространственно разделенных событий относительно. Из постулатов теории относительности и существования конечной скорости распространения сигналов следует, что в разных инерциальных системах отсчёта время протекает по-разному. Основное уравнение МКТ
1. Понятие идеального газа, его свойства. 2. Объяснение давления газа. 3. Необходимость измерения температуры. 4. Физический смысл температуры. 5. Температурные шкалы. 6. Абсолютная температура. Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. Идеальным принято считать газ, если: а) между молекулами отсутствуют силы притяжения, т. е. молекулы ведут себя как абсолютно упругие тела; б) газ очень разряжен, т. е. расстояние между молекулами намного больше размеров самих молекул; в) тепловое равновесие по всему объему достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрел свойства идеального, осуществляются при соответствующем разряжении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных. Основными параметрами идеального газа являются давление, объем и температура. Одним из первых и важных успехов МКТ было качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение заключается в том, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда. На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа, которое выглядит так:, где р — давление идеального газа, m0 — масса молекулы, среднее значение концентрация молекул, квадрата скорости молекул. Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа получим основное уравнение МКТ идеального газа в виде: Однако, измерив только давление газа, невозможно узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужно измерение еще какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной является температура. Температура — скалярная физическая величина, описывающая состояние термодинамического равновесия (состояния, при котором не происходит изменения микроскопических параметров). Как термодинамическая величина температура характеризует тепловое состояние системы и измеряется степенью его отклонения от принятого за нулевое, как молекулярно-кинетиче-ская величина — характеризует интенсивность хаотического движения молекул и измеряется их средней кинетической энергией. Ек = 3/2 kT, где k = 1,38 • 10^(-23) Дж/К и называется постоянной Больцмана. Температура всех частей изолированной системы, находящейся в равновесии, одинакова. Измеряется температура термометрами в градусах различных температурных шкал. Существует абсолютная термодинамическая шкала (шкала Кельвина) и различные эмпирические шкалы, которые отличаются начальными точками. До введения абсолютной шкалы температур в практике широкое распространение получила шкала Цельсия (за О °С принята точка замерзания воды, за 100 °С принята точка кипения воды при нормальном атмосферном давлении). Единица температуры по абсолютной шкале называется Кельвином и выбрана равной одному градусу по шкале Цельсия 1 К = 1 °С. В шкале Кельвина за ноль принят абсолютный ноль температур, т. е. температура, при которой давление идеального газа при постоянном объеме равно нулю. Вычисления дают результат, что абсолютный нуль температуры равен -273 °С. Таким образом, между абсолютной шкалой температур и шкалой Цельсия существует связь Т = t °C + 273. Абсолютный нуль температур недостижим, так как любое охлаждение основано на испарении молекул с поверхности, а при приближении к абсолютному нулю скорость поступательного движения молекул настолько замедляется, что испарение практически…
Поток вектора напряженности и его геометрический смысл. Теорема Остроградского-Гаусса (ОГ) для электростатического поля. Пример использования ОГ. Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля(Φ). Понятие потока вектора Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора
где
Полный поток вектора напряженности
где
Применение теоремы Остроградского–Гаусса особенно удобно для расчета электростатических полей симметричных систем зарядов. В этом случае можно так выбрать гауссову поверхность, что поток напряженности поля через нее легко выражается через искомое значение модуля вектора. Решение задачи о нахождении напряженности поля в какой-либо точке пространства должно осуществляться следующим образом: 1. Исходя из симметрии распределения заданной системы зарядов в пространстве необходимо построить силовые линии поля, т.е. определить направление вектора в любой точке пространства. 2. Выбрать “удобную” замкнутую гауссову поверхность, отвечающую следующим требованиям: а) она должна проходить через исследуемую точку; б) площадь поверхности должна быть известна; в) модуль напряженности поля должен быть постоянен в точках всей поверхности или хотя бы ее части; г) угол между и внешней нормалью к поверхности должен быть известен в любой точке поверхности (это обеспечивается выполнением п. 1). 3. Определить поток напряженности поля через выбранную поверхность.
Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Энергия W м магнитного поля катушки с индуктивностью L, создаваемого током I, равна W м = LI2/ 2
Дифракция на щели Пусть плоская монохроматическая волна падает на экран с узкой бесконечно длинной щелью. На рис. 1
Рис. 1
Рис. 2 Вторичные волны распространяются по всем направлениям от (0) до ( Рассмотрим лучи, которые идут под некоторым углом Если в
где m = 0; 1; 2;... Поскольку
На рис. 3 дано распределение интенсивности света при дифракции на щели в зависимости от угла. Её можно вычислить по формуле:
Рис. 3
Рис.6-2. Иллюстрация к закону поглощения Бугера. I0 – интенсивность световой волны, вступающей в вещество, d – толщина слоя вещества, пройденного светом, Коэффициент поглощения Для растворов закон Бугера принимает вид:
где, d – толщина слоя раствора, через который прошел свет, Коэффициент поглощения Цветные прозрачные тела, красители, растворы обнаруживают селективность (избирательность) поглощения в области видимых лучей, то есть различно поглощают лучи различных длин волн. Например, красными является стекло или раствор, слабо поглощающие красные и оранжевые лучи и сильно поглощающие зеленые и фиолетовые. В общем случае коэффициент
Рис.6-3. Зависимость коэффициента поглощения вещества от частоты света для газов и паров металлов при невысоких давлениях. Рис.6-4. Зависимость коэффициента поглощения вещества от частоты света для жидкостей, твердых тел, а также для газов при высоком давлении Тепловое излучение Определение, механизм и основные характеристики теплового излучения. Одним из наиболее распространенных источников и механизмов порождения электромагнитного излучения является тепловое возбуждение атомов (молекул, ионов) вещества. При хаотическом тепловом движении, вследствие взаимодействий – “соударений”, часть атомов может переходить в возбужденное состояние, характеризующееся избыточным, по сравнению со стационарным (невозбужденным) состоянием, значением энергии. Возбужденное состояние атома является неустойчивым, и он самопроизвольно переходит в более устойчивое – энергетически более низкое – состояние, избавляясь от избытка энергии путем излучения электромагнитных волн, которые и называют тепловым излучением. При комнатной температуре тела испускают электромагнитные волны преимущественно в инфракрасном диапазоне частот. С ростом температуры появляется красный, затем желтый и, наконец, фиолетовый цвет свечения. Интенсивность теплового излучения, очевидно, должно сильно зависеть от температуры, являющейся мерой теплового (внутреннего) движения атомов вещества. Кроме того, тепловое излучение твердых тел оказывается неравномерно распределенным по спектру[1] частот (длин волн), который у твердых тел оказывается сплошным (непрерывным). Важнейшими характеристиками излучающего тела являютсяизлучательная способность (или излучательность) El, Т и поглощательная способность (коэффициент поглощения) al, Т. Излучательная способность El, Т тела, представляет собой спектральную плотность потока энергии теплового излучения, т. е. энергию, излучаемую телом в единицу времени с единицы площади в единичном интервале длин волн (или частот): El, Т = dE/(dS×dt×dl) = dР/dS×dl. [Дж/(м2×с×м) = Вт/м3] Мощность Р излучения в оптике часто называют световым потоком Ф или, иногда – интенсивностью I света.. [Дж/(м2×с×м) = Вт/м3] Т. к. n = с/l, то dn = - с×dl/l2 и от распределения излучательности по длинам волн можно перейти к распределению ее по спектру частот: |En, Т| = El, Т ×l2/с; |El, Т| = En, Т ×с/l2 = En, Т ×n2/с. Основной задачей в оптике теплового излучения является определение в явном виде его спектра, т. е. вида функции El, Т или En, Т. Опытным путем во второй половине XIX в. был установлен общий вид этой функции, характерным для которого было наличие максимума, зависящего от температуры (см рис.). Теоретически же получить вид этой функции долго не удавалось. Один из первых шагов на пути решения основной задачи теории теплового излучения был сделан в 1859 г. Р. Кирхгофом. Законы теплового излучения АЧТ. Распределение энергии излучения АЧТ по спектру. Квантовая модель излучения Планка. Законы теплового излучения Между излучательностью
где Величины Для абсолютно черного тела Из закона Кирхгофа вытекает, что телом сильнее испускаются и поглощаются излучения одних и тех же длин волн. Поглощательная способность серых тел при данной температуре постоянна и не зависит от длины волны. По закону Кирхгофа (1.6) для серого тела
Планк нашел зависимость спектральной плотности излучательности абсолютно черного тела от длины волны и температуры. Эта зависимость выражается формулой Планка:
где Графическая зависимость
Рис. 1.2. Распределение энергии в спектре
Энергетическая светимость абсолютно черного тела равна площади, ограниченной кривой зависимости
где Энергетическая светимость серого тела:
Длина волны
Это соотношение называется законом смещения Вина. Из (1.11) следует, что при повышении температуры максимум спектральной плотности излучения смещается в область более коротких волн (рис. 1.2). Максимальная спектральная плотность энергетической светимости абсолютно черного тела возрастает пропорционально пятой степени температуры где Выражение (1.12) – закон о максимуме спектральной плотности энергетической светимости (излучательности) Вина.
Законы изучения АЧТ. На основании экспериментальных данных были получены следующие законы:
Выясним, что представляют собой величины в формулах (§) и (§§) на графике зависимости излучательной способности АЧТ ro от длины волны l.
Квантовая модель Макса Планка «С 1896 года Макс Планк заинтересовался измерениями, производившимися в Государственном физико-техническом институте в Берлине, а также проблемами теплового излучения тел. Любое тело, содержащее тепло, испускает электромагнитное излучение. Если тело достаточно горячее, то это излучение становится видимым. При повышении температуры тело сначала раскаляется докрасна, затем становится оранжево-жёлтым и, наконец, белым. Излучение испускает смесь частот (в видимом диапазоне частота излучения соответствует цвету). Однако излучение тела зависит не только от температуры, но и до некоторой степени от таких характер
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.99.221 (0.013 с.) |




 и
и  и скорости до взаимодействия
и скорости до взаимодействия  , а после взаимодействия (столкновения)
, а после взаимодействия (столкновения) 



 и (в некоторой системе отсчёта К) радиус-векторы
и (в некоторой системе отсчёта К) радиус-векторы  :
:

 — импульсы частиц), которую можно использовать для перехода от данной системы отсчёта Кк системе центра масс, вычисляя скорости и радиус-векторы частиц в ней по формулам:
— импульсы частиц), которую можно использовать для перехода от данной системы отсчёта Кк системе центра масс, вычисляя скорости и радиус-векторы частиц в ней по формулам:



 — это линейное преобразование
— это линейное преобразование  , сохраняющее индефинитное скалярное произведение векторов. Это означает, что для любых двух векторов
, сохраняющее индефинитное скалярное произведение векторов. Это означает, что для любых двух векторов  выполняется равенство
выполняется равенство
 в псевдоевклидовом пространстве
в псевдоевклидовом пространстве  . Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1)потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами нет дальнодействующих сил притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют форму упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц[1]. В рамках термодинамикиидеальными называются гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состоянияКлапейрона — МенделееваИдеальный газ. Основное уравнение МКТ идеального газа. Температура и ее измерение. Абсолютная температура.
. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1)потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами нет дальнодействующих сил притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. В расширенной модели идеального газа частицы, из которого он состоит, имеют форму упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц[1]. В рамках термодинамикиидеальными называются гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состоянияКлапейрона — МенделееваИдеальный газ. Основное уравнение МКТ идеального газа. Температура и ее измерение. Абсолютная температура. аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора
аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора  к площадке называется элементарным потоком вектора напряженности через площадку ΔS:
к площадке называется элементарным потоком вектора напряженности через площадку ΔS: ,
, – проекция вектора
– проекция вектора  ;
;  К определению элементарного потока ΔΦ.
К определению элементарного потока ΔΦ. в общем случае равен:
в общем случае равен:
 . (Выбор нормали
. (Выбор нормали 

 -- проекция экрана со щелью
-- проекция экрана со щелью  на плоскость рисунка. Ширина щели (
на плоскость рисунка. Ширина щели ( ) имеет размер порядка длины волны света. Щель
) имеет размер порядка длины волны света. Щель 

 ) к направлению распространения волн (рис. 1). Если за щелью поставить линзу, то все лучи, которые шли до линзы параллельно, соберутся в одной точке фокальной плоскости линзы. В этой точке наблюдается интерференция вторичных волн. Результат интерференции зависит от числа длин полуволн, которое укладывается в разности хода между соответствующими лучами.
) к направлению распространения волн (рис. 1). Если за щелью поставить линзу, то все лучи, которые шли до линзы параллельно, соберутся в одной точке фокальной плоскости линзы. В этой точке наблюдается интерференция вторичных волн. Результат интерференции зависит от числа длин полуволн, которое укладывается в разности хода между соответствующими лучами. к направлению падающей световой волны (рис. 2).
к направлению падающей световой волны (рис. 2).  -- разность хода между крайними лучами. Разобьем
-- разность хода между крайними лучами. Разобьем  отличается на
отличается на  ).
). уложиться четное число длин полуволн, то в точке
уложиться четное число длин полуволн, то в точке  . Если нечетное, то усиление света --
. Если нечетное, то усиление света --  .
.
 (см. рис. 2), то эти условия можно записать в следующем виде:
(см. рис. 2), то эти условия можно записать в следующем виде:

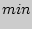






 - коэффициент поглощения, зависящий от длины световой волны, химической природы и состояния вещества.
- коэффициент поглощения, зависящий от длины световой волны, химической природы и состояния вещества. – физическая величина, обратно пропорциональная слою вещества, при прохождении которого интенсивность падающего света убывает в е (е = 2,7) раз. При измерении коэффициента поглощения необходимо учитывать, что часть света отражается от границы исследуемого вещества. Закон справедлив при не слишком больших интенсивностях света и только для монохроматического излучения, так как для каждого вещества
– физическая величина, обратно пропорциональная слою вещества, при прохождении которого интенсивность падающего света убывает в е (е = 2,7) раз. При измерении коэффициента поглощения необходимо учитывать, что часть света отражается от границы исследуемого вещества. Закон справедлив при не слишком больших интенсивностях света и только для монохроматического излучения, так как для каждого вещества  зависит от длины волны
зависит от длины волны  .
.
 – коэффициент поглощения, не зависящий от концентрации С и характерный только для молекулы поглощающего вещества.
– коэффициент поглощения, не зависящий от концентрации С и характерный только для молекулы поглощающего вещества.  , где I – интенсивность излучения,прошедшего поглощающую среду; I0 – интенсивность падающего излучения. Оптическая плотность может быть определена и как логарифм величины, обратнойкоэффициенту пропускания
, где I – интенсивность излучения,прошедшего поглощающую среду; I0 – интенсивность падающего излучения. Оптическая плотность может быть определена и как логарифм величины, обратнойкоэффициенту пропускания  , т.е., D = lg (1/
, т.е., D = lg (1/  ).
).
 зависит от длины волны (или частоты) света. Поглощение велико лишь в области частот, близких к частотам собственных колебаний электронов в атомах. У веществ, атомы (молекулы) которых практически не взаимодействуют (газы и пары металлов при невысоком давлении), коэффициент поглощения для большинства длин волн близок к нулю, и лишь для очень узких областей спектра имеет резкие максимумы (рис.6-3). Эти максимумы соответствуют резонансным частотам колебаний электронов. Газы при высоких давлениях, жидкости и твердые тела дают широкие полосы поглощения (рис.6-4).
зависит от длины волны (или частоты) света. Поглощение велико лишь в области частот, близких к частотам собственных колебаний электронов в атомах. У веществ, атомы (молекулы) которых практически не взаимодействуют (газы и пары металлов при невысоком давлении), коэффициент поглощения для большинства длин волн близок к нулю, и лишь для очень узких областей спектра имеет резкие максимумы (рис.6-3). Эти максимумы соответствуют резонансным частотам колебаний электронов. Газы при высоких давлениях, жидкости и твердые тела дают широкие полосы поглощения (рис.6-4).

 и поглощательной способностью
и поглощательной способностью  существует взаимосвязь, установленная Кирхгофом. Отношение излучательности тела к его поглощательной способности для произвольной длины волны и температуры одинаково для всех тел и равно спектральной плотности излучения абсолютно черного тела:
существует взаимосвязь, установленная Кирхгофом. Отношение излучательности тела к его поглощательной способности для произвольной длины волны и температуры одинаково для всех тел и равно спектральной плотности излучения абсолютно черного тела: , (1.6)
, (1.6) – спектральная плотность излучения, зависящая только от длины волны и температуры.
– спектральная плотность излучения, зависящая только от длины волны и температуры. ,поэтому из закона Кирхгофа (1.6) вытекает, что
,поэтому из закона Кирхгофа (1.6) вытекает, что  . Таким образом, универсальная функция Кирхгофа
. Таким образом, универсальная функция Кирхгофа  (1.7)
(1.7) , (1.8)
, (1.8) Джс – постоянная Планка,
Джс – постоянная Планка,  Дж/К – постоянная Больцмана,
Дж/К – постоянная Больцмана,  м/с – скорость света в вакууме.
м/с – скорость света в вакууме. при некоторой температуре
при некоторой температуре  представлена на рис. 1.2, где изображены две кривые, соответствующие двум разным температурам
представлена на рис. 1.2, где изображены две кривые, соответствующие двум разным температурам  и
и  , причем
, причем 
 , (1.9)
, (1.9) = 5,6710-8 Втм-2 (К)-4 – постоянная Стефана–Больцмана.
= 5,6710-8 Втм-2 (К)-4 – постоянная Стефана–Больцмана. . (1.10)
. (1.10) , на которую приходится максимум спектральной плотности излучения
, на которую приходится максимум спектральной плотности излучения  . (1.11)
. (1.11) мК – постоянная закона смещения Вина.
мК – постоянная закона смещения Вина. , (1.12)
, (1.12) .
. На рисунке приведена зависимость излучательной способности АЧТ от длины волны при различных температурах. Эти данные получены экспериментально. Из графиков видно, что энергия распределяется по длинам волн неравномерно, с увеличением температуры излучение резко возрастает. При указанных температурах максимумы излучения попадают в инфракрасный диапазон длин волн, на видимую область (0,4-0,75 мкм) приходится незначительное количество энергии [v]. С ростом температуры максимумы смещаются в сторону более коротких длин волн. На втором рисунке приведен для сравнения спектр солнечного излучения. «Провалы» в спектре – это линии поглощения атмосферой, огибающая – спектр излучения АЧТ.
На рисунке приведена зависимость излучательной способности АЧТ от длины волны при различных температурах. Эти данные получены экспериментально. Из графиков видно, что энергия распределяется по длинам волн неравномерно, с увеличением температуры излучение резко возрастает. При указанных температурах максимумы излучения попадают в инфракрасный диапазон длин волн, на видимую область (0,4-0,75 мкм) приходится незначительное количество энергии [v]. С ростом температуры максимумы смещаются в сторону более коротких длин волн. На втором рисунке приведен для сравнения спектр солнечного излучения. «Провалы» в спектре – это линии поглощения атмосферой, огибающая – спектр излучения АЧТ.







