Кинематика движения материальной точки по окружности. Характеристики движения: вектор элементарного поворота,угловаяскорость, ускорение и их связь с линейной скоростью и ускорением.
Похожие статьи вашей тематики
2.1Движения Материальной Точки по Окружности
Движение точки по окружности может быть очень сложным (рис. 17).
Рассмотрим подробно движение точки по окружности, при котором v = const. Такое движение называется равномерным движением по окружности. Естественно, вектор скорости не может быть неизменным (v не равно const), так как направление скорости постоянно меняется.
Время, за которое траектория точки опишет окружность, называется периодом обращения точки (Т). Число оборотов точки в одну секунду называется частотой обращения (v). Период обращения можно найти по формуле:

Естественно, перемещение точки за один оборот будет равно нулю. Однако пройденный путь будет равен 2ПиR, а при числе оборотов п путь будет равен 2ПиRn или 2ПиRt/T, где t - время движения.
Ускорение при равномерном движении точки по окружности направлено к ее центру и численно равно а = v2/R.
Это ускорение называется центростремительным (или нормальным). Вывод этого равенства может быть следующим. Приведем векторы скорости к одной точке хотя бы за - Т (можно и за Т/2 или Т) Тогда сумма изменений векторов скоростей за малые промежутки времени будет равна длине дуги АВ, которая равна модулю |v2 - v1| за время t = 1/4*Т.
Определим длину дуги. Поскольку радиусом для дуги будет модуль вектора v1=v2=v, то длина дуги l может быть вычислена как длина четверти окружности с радиусом v:
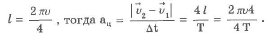
После сокращения получим: 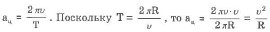
Если же движение равнопеременное, то v Ф const, тогда рассматривают другую составляющую ускорения, обеспечивающую изменение модуля скорости. Это ускорение называется тангенциальным:

Тангенциальное ускорение направлено по касательной к траектории, оно может совпадать по направлению со скоростью (движение равноускоренное) или быть противоположно направленным (движение равнозамедленное).
2.2Скорости движения различных точек тела, вращающегося вокруг неподвижной оси, различаются. Поэтому для описания вращения твердого тела вводят угловые величины, относящиеся ко всему телу в целом, а не к отдельным его точкам. Такими величинами являются угол поворота j, угловая скорость и угловое ускорение тела.
Вектор угловой скорости тела определяют в виде
 , (1.18) , (1.18)
где dt – промежуток времени, за который тело совершает поворот  . Вектор . Вектор 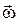 совпадает по направлению с вектором совпадает по направлению с вектором  . .
Изменение вектора 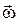 со временем характеризуют вектором углового ускорения со временем характеризуют вектором углового ускорения 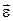 , который определяют в виде , который определяют в виде
 . (1.19) . (1.19)
Направление вектора 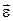 совпадает с направлением приращения совпадает с направлением приращения  вектора вектора  . .
Единицей угловой скорости в СИ является радиан в секунду (рад/с), а единицей углового ускорения – радиан на секунду в квадрате (рад/с2).
Используя определения (1.18) и (1.19), получим выражения для проекций угловой скорости и углового ускорения wz и ez на ось вращения z, (рис. 1.7)
 ; ;  Формулы для расчета w(t) и j(t).можно получить интегрированием (1.20) Формулы для расчета w(t) и j(t).можно получить интегрированием (1.20)
j(t) = wzt + j0;wz(t) = ezt + wz0. (1.21)
Выразим скорость 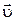 произвольной точки твердого тела, вращающегося вокруг неподвижной оси, через угловую скорость произвольной точки твердого тела, вращающегося вокруг неподвижной оси, через угловую скорость  . Пусть положение точки М относительно некоторой точки О оси вращения характеризуется радиусом-вектором r (рис. 1.10). Разделим обе части формулы (1.17) на dt. Т. к. . Пусть положение точки М относительно некоторой точки О оси вращения характеризуется радиусом-вектором r (рис. 1.10). Разделим обе части формулы (1.17) на dt. Т. к. 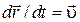 и и  , то искомое выражение примет вид , то искомое выражение примет вид
 , (1.22) , (1.22)
Модуль вектора скорости в формуле
u = wR, (1.23)
где R – радиус окружности, по которой движется точка М.
Найдем полное ускорение  точки М. Для этого продифференцируем (1.22) по времени точки М. Для этого продифференцируем (1.22) по времени
 Þ Þ  . (1.24) . (1.24)
В данном случае ось вращения неподвижна, и векторы 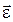 и и  параллельны. Вектор параллельны. Вектор  представляет собой тангенциальное ускорение представляет собой тангенциальное ускорение 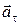 . Вектор . Вектор  является нормальным ускорением является нормальным ускорением  . Модули этих ускорений равны . Модули этих ускорений равны
at = eR; an = w2R.
Модуль полного ускорения
 . .
Для решения задач, в которых вращение тела является равномерным, используются также понятия периода и частоты вращения. Периодом вращения Т называют промежуток времени, в течение которого тело, вращаясь с постоянной угловой скоростью w, совершает один полный оборот, т. е. поворачивается на угол j = 2p. Частотой вращения п называют число оборотов, совершаемых телом за 1 с при равномерно вращении с угловой скоростью w.
|