Гармонические механические колебания . Уравнение и характеристики гармонического осциллятора . Энергия механический колебаний.
Похожие статьи вашей тематики
Пусть материальная точка осуществляет прямолинейные гармонические колебания вдоль оси координат х вокруг положения равновесия, которое принято за начало координат. Тогда зависимость координаты х от времени t определяется уравнением:
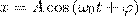 (1) (1)
Продифференцировав (1) получим, что скорость ν и ускорение а колеблющейся точки равны соответственно
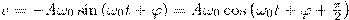
 (2) (2)
Сила F=ma, которая действует на колеблющуюся материальную точку массой m, с учетом (1) и (2) будет равна

Значит, сила прямо пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (т.е. к положению равновесия).
Кинетическая энергия материальной точки, которая совершает прямолинейные гармонические колебания:
 (3) (3)
или
 (4) (4)
Потенциальная энергия материальной точки, которая совершает гармонические колебания под действием упругой силы F, будет равна
 (5) (5)
или
 (6) (6)
Сложив (3) и (5), найдем выражение для полной энергии:
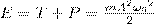 (7) (7)
Полная энергия всегда остается постоянной, так как при гармонических колебаниях выполняется закон сохранения механической энергии, т.к. упругая сила консервативна.
Из формул (4) и (6) вытекает, что Т и P изменяются с частотой 2ω0, т. е. с частотой, которая в два раза превышает частоту гармонического колебания. На рис. 1 даны графики зависимости x, T и P от времени. Так как <sin2α> = <cos2α> = 1/2, то из формул (3), (5) и (7) вытекает, что <T> = <P> = E/2.

Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается (затухает).
Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления)
,
где r – коэффициент сопротивления, – скорость движения.
Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x:
,
где kx – возвращающая сила, rυx – сила трения. Это уравнение можно переписать:
, отсюда следует:.
Введем обозначения:;.
Тогда однородное дифференциальное уравнение второго порядка, описывающее затухающее колебательное движение, запишем так:
Решение уравнения (3.1.1) имеет вид (при):
Здесь А0 и φ0 определяются из краевых условий задачи (начальных и граничных), а β и ω – из самого уравнения.
Найдем круговую частоту ω. Здесь она уже не равна.
Для этого найдем первую и вторую производные от x:
,
Подставим эти значения в (3.1.1) и сократим на:
.
Сократим на и выразим ω:
,
,
где ω0 – круговая частота собственных колебаний (без затухания); ω – круговая частота свободных затухающих колебаний. Из этого выражения ясно, почему решение (3.1.1) будет только при.
Для колебаний под действием различных сил (квазиупругих) значения ω, β, ω0 будут различными. Например, для колебаний под действием упругой силы
;;
Затухающие колебания представляют собой непериодические колебания, так как в них не повторяется, например, максимальное значение амплитуды. Поэтому называть ω –циклической (повторяющейся, круговой) частотой можно лишь условно. По этой же причине и
называется условным периодом затухающих колебаний.
Векторный способ представления колебаний. Сложение двух гармонических колебаний одного направления. Биения.
Если материальная точка участвует одновременно в двух гармонических колебаниях с одинаковой циклической частотой, то происходит сложение гармонических колебаний. Рассмотрим несколько наиболее простых случаев сложения гармонических колебаний.
1. Круговые частоты и фазы колебаний одинаковы, амплитуды различны: x1=A1sinφ, x2=A2sinφ
тогда x1 + x2 = (A1 + A2)sinφ = Asinφ
2. Круговые частоты и амплитуды одинаковы, фазы различны: x1=A?sinφ, x2=A?sinφ
где φ — разность фаз. Тогда

В результате возникает гармоническое колебание такой же частоты, но отличающееся по фазе от первичных колебаний на половину разности фаз этих колебаний. Амплитуда меньше суммы амплитуд первичных колебаний.
3. Амплитуды одинаковы, круговые частоты мало отличаются друг от друга: x1=A?sinφ, x2=A?sinφ, тогда результирующее колебание оказывается не гармоническим, так как оно не соответствует уравнению x = Asinφ
|