
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Периодические процессы. Гармонические колебания. Уравнения колебаний. Энергия колебаний.Стр 1 из 6Следующая ⇒
Периодические процессы. Гармонические колебания. Уравнения колебаний. Энергия колебаний.
 Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени. Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени.
Амплитуда – модуль максимального отклонения от положения равновесия.
Движение любой сложной системы можно представить как суперпозицию более простых движений, называемых модами.
Энергия гармонических колебаний.
Гармонический осциллятор – система, совершающая гармонические колебания около положения равновесия, к-ые описываются ур-нием вида
|
Собственные колебания механических систем. Маятники

Пружинный маятник – груз массой m на абсолютно упругой пружине совершает колебания под действием упругой силы.
Таким образом М опережает по фазе смещение на
Математический маятник – это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешен точечный груз массой m, совершающий колебания под действием силы тяжести.
при малых углах
Гюйгенс
Физический маятник
Приведённая длина физ. маятника – длина такого мат. маятника, период колебаний к-ого совпадает с периодом колебаний данного физ. маятника. Th Штейнера:
Момент инерции J относ. произвольной оси равен моменту его инерции J0 относ. параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела m на квадрат расстояния l между осями.
Точка на прямой, соединяющей т. подвеса с центром инерции (масс) на расстоянии пр. длины от оси вращения, - центр качаний физ. маятника. Можно показать, что если подвесить физ. маятник в центре качаний, то пр. длина и T будут такими же, как и в начале.
|
Затухающие колебания
 Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса.
В любой реальной колебательной системе существуют потери энергии, поэтому колебания будут уже не гармоническими, т.к. это не периодический процесс. Если потери небольшие, то можно приближённо ввести понятие периода затухающих колеб., к-ый будет несколько больше периода незатухающих колеб. Можно показать, что при малых энергетических потерях сила сопротивления прямо пропорциональна скорости:
где
При демпфировании система быстрее всего приходит в положение равновесия.
декремент затухания
логарифмический декремент Добротность Q прямо пропорц. числу колеб. за время, за к-ое амплитуда уменьшается в e раз (τ)
| |||||||||||||||
| ··1·· | ··2·· | ··3·· |
Заголовок В качестве естественных дифракционных решёток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с λ рентгеновского излучения (Лауэ).
Вульф и Брэггам предположили, что дифракция рентгеновского излучения является результатом его отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решётки).
Рентгеновское излучение – электромагнитные волны 5-4*10-3нм. Распр источник – рентгеновская трубка. Представим кристаллы в виде совокупности параллельных кристаллографических плоскостей, отстоящих др. от др. на d. Пучок параллельных монохроматических рентгеновских лучей падает под углом скольжения θ (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы крист решётки, к-ые становятся источниками когерентных вторичных волн, интерферирующих между собой. Дифракционные максимумы наблюдаются в тех направлениях, в к-ых все отражённые атомными плоскостями волны будут находиться в одинаковой фазе.
Формула Вульфа-Брэггов:
m=1,2,3… т.е. при разности хода между 2 лучами, отражёнными от соседних кристаллографических плоскостей, кратному целому числу длин волн λ, наблюдается дифф макс. | |||||||||||||||||||||||||
| ··25·· | ··26·· | ··27·· | |||||||||||||||||||||||
Дисперсия света
Дисперсия света - разложение света в спектр при его преломлении в среде и дифракции. Дисперсия обусловлена зависимостью показателя преломления n вещества от частоты υ света. Если вынужденное излучение попадает в вещ-во, то оно вызывает колебания свободных эл зарядов. Эти колебания вызывает появление вторичных волн, к-ые распространяются во все стороны с частотой вынужденных колебаний υ, однако возникает суммарная эм волна, к-ая распространяется в данной среде с υ, но имеет свою амплитуду, фазу и скорость распространения, к-ые зависят от частоты падающей первоначальной волны.
Первые экспериментальные наблюдения дисперсии – Ньютон (1672) – дисперсия белого света в призме.
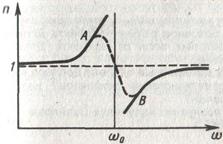
Показатель преломления для прозрачных вещ-в с уменьшением длины волны увеличивается. Следовательно дисперсия D=dn/dλ увеличивается. Это нормальная дисперсия.
т.к. μ в оптической обл спектра = 1.
AB – область аномальной дисперсии ω↑→ω0=>r0↑=>p↑=> pполн↑=>↑ε=1+pполн/ε0ε=>↑n. В металлах ω0=0
если ω<ωкр, то n-мнимое, ω>ωкр.
|
Эффект Комптона. Эффект Комптона. Рассеивание рентгеновских и гамма лучей-эффект Комптона.
=
Эффект Комптона легко объясняется если рассмотрев рассеивание как процесс упругого столкновения рентгеновских фотонов с покоящимися электронами.

|
Заголовок
 Текст Текст | |||||||||||||||||||||||
| ··44-49·· | ··44·· | ··45·· |
Периодические процессы. Гармонические колебания. Уравнения колебаний. Энергия колебаний.
|
 Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени.
Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени.
Амплитуда – модуль максимального отклонения от положения равновесия.
 ,
,  - фаза колебаний.
- фаза колебаний.
 - для системы с 1 ст. свободы
- для системы с 1 ст. свободы 


 - уравнение гармонических колебаний.
- уравнение гармонических колебаний.
Движение любой сложной системы можно представить как суперпозицию более простых движений, называемых модами.
Энергия гармонических колебаний.




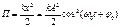



Гармонический осциллятор – система, совершающая гармонические колебания около положения равновесия, к-ые описываются ур-нием вида 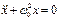 .
.
|
|
| Поделиться: |
Последнее изменение этой страницы: 2016-12-12; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.252.8 (0.32 с.)



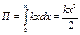

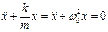

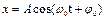


 . Ускорение и смещение находятся в противофазе.
. Ускорение и смещение находятся в противофазе.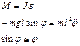




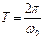 ,
, 
 ,
, 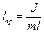



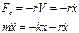



 ,
,
 =
=  - условие демпфирования,
- условие демпфирования,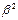 >
>  - апериодический процесс.
- апериодический процесс. ,
,  - время, через к-ое амплитуда колебаний уменьшается в e раз (время релаксации).
- время, через к-ое амплитуда колебаний уменьшается в e раз (время релаксации).





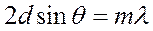
 n=f(υ)
n=f(υ)
 ,
,










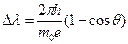
 - постоянная Комптанта = 0,0242 [А]Амстрем
- постоянная Комптанта = 0,0242 [А]Амстрем



