
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон электромагнитной индукции как следствие закона сохранения энергииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основной закон электромагнитной индукции гласит, что индукционный ток возникает в проводящем контуре при всяком изменении магнитного потока, пронизывающего поверхность, охваченную этим контуром. Однако, производя Это обстоятельство приводит к мысли, что при неизменных условиях опыта в катушке индуцируется определенная э. д. с, а сила тока, возникающего благодаря этому, определяется законом Ома и поэтому оказывается обратно пропорциональной электрическому сопротивлению цепи. Действительно, нетрудно осуществить простой опыт, Заменив лампочку тепловым амперметром (§ 44), мы можем измерить силу индукционного тока; измеряя, кроме того, полное сопротивление всей цепи, мы убедимся в том, что и для индукционных токов справедлив закон Ома (§ 46): С понятием э. д. с. мы встречались уже раньше при рассмотрении вопроса об условиях возникновения и поддержания электрического тока в цепи (§ 39). Существенное различие между случаями, рассмотренными ранее (гл. VI), и э. д. с. индукции заключается в следующем. В случае гальванического элемента, аккумулятора или термоэлемента мы могли установить, что э. д. с. возникает в определенных местах цепи тока, именно, в пограничном слое между металлом и электролитом или в месте контакта двух различных металлов. В случае же индукции э. д. с. не сосредоточена в том или ином участке цепи, но действует во всей индукционной цепи в целом, т. е. во всех точках цепи, где изменяется поток магнитной индукции. В случае витка, охватывающего линии поля, э. д. с. возникает во всех точках витка и может быть подсчитана для витка в целом. В случае нескольких витков то же происходит в каждом из них: э. д. с. катушки складывается из э. д. с. отдельных витков. Правило ленца Правило Ленца отражает тот экспериментальный факт, что Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам. 1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы. Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле
На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью
Работа силы FЛ на пути l равна
По определению ЭДС
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для
Для того, чтобы установить знак в формуле, связывающей Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный Iинд =
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника. 2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не являетсяпотенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физикомДж. Максвеллом в 1861 г. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1021; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.013 с.) |




 обозначена э. д. с. индукции, остающаяся неизменной при изменении сопротивления цепи в наших опытах.
обозначена э. д. с. индукции, остающаяся неизменной при изменении сопротивления цепи в наших опытах. инд и
инд и  всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии. перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью
перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью  по двум другим сторонам (рис. 1.20.3).
по двум другим сторонам (рис. 1.20.3).

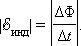
 нужно выбрать согласованные между собой по правилу правого буравчика направление нормали
нужно выбрать согласованные между собой по правилу правого буравчика направление нормали  и положительное направление обхода контура
и положительное направление обхода контура  как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
 . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
. Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна



