
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярные электрические токи. Атом в магнитном поле. Объяснение природы диа- и парамагнетизма.Содержание книги
Поиск на нашем сайте
Существование спина – собственного момента импульса неподвижной элементарной частицы следует из законов релятивисткой квантовой механики. Если частица заряжена, то с её спином связан магнитный момент, величина которого также определяется магнетоном Бора (8.1). Нуклоны атомного ядра участвуют как в орбитальном, так и в спиновом движении. Порядок величины соответствующих магнитных моментов определяется ядерным магнетоном
где Таким образом, в качестве источников магнитного поля вещества рассматриваются магнитные моменты элементарных частиц, образующих атомы. Поскольку ядерный магнетон (8.2) почти на три порядка меньше магнетона Бора (8.1), то в дальнейшем ядерный магнетизм не учитывается. Для вещества в состоянии термодинамического равновесия суммарный магнитный момент всех атомов равен нулю. При включении внешнего магнитного поля орбитальное и спиновое движения атомных электронов меняются. В классической электродинамике эти измененные движения определяютмолекулярные токи, индуцированные магнитным полем. При макроскопическом подходе индуцированные микроскопические токи в атомах усредняются по объему, содержащему большое число атомов, и вводятся так называемые токи намагничивания
С помощью токов намагничивания описывается отклик вещества на внешнее магнитное поле. Под действием магнитного поля атомы приобретают индуцированные магнитные моменты, ориентация которых определяется направлением этого магнитного поля. В результате суммарный магнитный момент единицы объема вещества, называемый намагниченностью,
становится отличным от нуля. Здесь Намагниченность и токи намагничивания связаны между собой интегральным соотношением
представляющим собой теорему о циркуляции вектора намагниченности. В правую часть равенства (8.5) входит алгебраическая сумма токов намагничивания, пересекающих поверхность, натянутую на контур L. С учетом как токов проводимости, создаваемыми свободными зарядами в проводниках, так и токов намагничивания, создаваемых связанными зарядами в веществе, теорема о циркуляции векторного поля магнитной индукции
Обычно внешнее магнитное поле создается с помощью токов проводимости, поэтому эти токи являются известными. Токи намагничивания необходимо определять с помощью заданных магнитных свойств вещества и внешнего магнитного поля. Для удобства расчета намагниченного вещества вводится новая характеристика магнитного поля
которая называется напряженностью магнитного поля. В системе СИ размерность напряженности магнитного поля ампер/метр (А/м). Из (8.5) – (8.7) следует теорема о циркуляции вектора напряженности магнитного поля
Здесь в правую часть входят известные токи проводимости При внесении атома в магнитное поле с индукцией
При этом изменяется орбитальный момент импульса электрона:
Аналогично изменяется вектор орбитального магнитного момента электрона:
Из этого следует, что векторы
Рис. 6.2 Эта прецессия называется ларморовской прецессией. Угловая скорость этой прецессии
Теорема Лармора: единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора Прецессия орбиты электрона в атоме приводит к появлению дополнительного орбитального тока, направленного противоположно току I:
и соответствующего ему наведенного орбитального магнитного момента
где
В диамагнитных материалах, помещенных во внешнее магнитное поле В0, возникают намагниченность и внутреннее поле, направленное навстречу намагничивающему полю. В молекулах диамагнитных веществ результирующие магнитные моменты, как орбитальные, так и спиновые, равны нулю. Поэтому суммарный магнитный момент диамагнитного поля также равен нулю. Движение электронов, которое создает магнитный момент молекулы, часто уподобляют электрическому току и называют молекулярным током. Когда диамагнитное тело помещают во внешнее магнитное поле, то вследствие вихревого характера магнитного поля в диамагнетике индуцируются незатухающие молекулярные токи. Эти молекулярные токи, по правилу Ленца, имеют такое направление, что созданное ими внутреннее магнитное поле стремится ослабить внешнее магнитное поле. Диамагнитный эффект присущ всем без исключения веществам, в том числе и парамагнетикам, но в парамагнетиках его превышает эффект, обусловленный ориентацией магнитных моментов отдельных молекул. Молекулы парамагнетика, имеющие орбитальный и спиновый магнитные моменты, попадая во внешнее магнитное поле, ориентируются в нем таким образом, что собственное поле парамагнетика усиливает внешнее намагничивающее поле. Поэтому магнитная восприимчивость диамагнетика отрицательна, а парамагнетика — положительна. Если диамагнитный эффект не зависит от температуры, то парамагнитный зависит, так как тепловое движение атомов или моле (11.12) кул разрушает ориентацию их магнитных моментов во внешнем магнитном поле. Зависимость магнитной восприимчивости % парамагнетиков от температуры выражается формулой Х = т, (11.15) где С — константа данного вещества, Т — его абсолютная температура. Это выражение называется законом Кюри. Закону Кюри подчиняются газообразный (парамагнитный) кислород, разбавленные жидкие растворы парамагнитных солей и некоторые парамагнитные соли в кристаллическом состоянии. При очень низких температурах наблюдаются отступления от закона Кюри.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.71.166 (0.007 с.) |

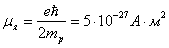 (8.2)
(8.2)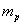 - масса протона. Интересно отметить, что магнитный момент электрически нейтрального нейтрона отличен от нуля, что объясняется кварковой структурой нейтрона.
- масса протона. Интересно отметить, что магнитный момент электрически нейтрального нейтрона отличен от нуля, что объясняется кварковой структурой нейтрона.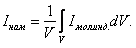 (8.3)
(8.3)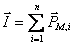 (8.4)
(8.4)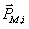 - магнитный момент i-ого элемента и n-число атомов в единице объем. В системе СИ намагниченность имеет размерность ампер/метр (А/м).
- магнитный момент i-ого элемента и n-число атомов в единице объем. В системе СИ намагниченность имеет размерность ампер/метр (А/м).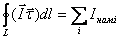 , (8.5)
, (8.5)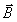 принимает вид
принимает вид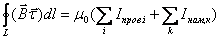 . (8.6)
. (8.6)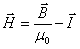 , (8.7)
, (8.7)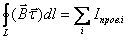 . (8.8)
. (8.8)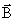 на электрон, движущийся по орбите, эквивалентной замкнутому контуру с током, действует момент сил
на электрон, движущийся по орбите, эквивалентной замкнутому контуру с током, действует момент сил 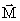 :
: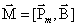 ,
,
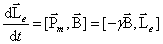 ,
,
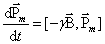 ,
,
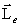 и
и 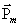 , и сама орбита прецессирует вокруг направления вектора
, и сама орбита прецессирует вокруг направления вектора 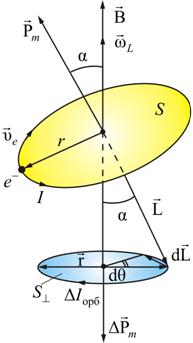
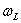 зависит только от индукции магнитного поля и совпадает с ней по направлению.
зависит только от индукции магнитного поля и совпадает с ней по направлению.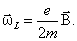 ,
,
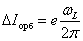 ,
,
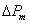 :
: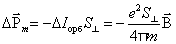 ,
,
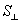 – площадь проекции орбиты электрона на плоскость, перпендикулярную вектору
– площадь проекции орбиты электрона на плоскость, перпендикулярную вектору 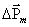 противоположен вектору
противоположен вектору 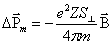 ,
,



