
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет интерференционной картины от двух источниковСодержание книги
Поиск на нашем сайте
Рассмотрим более подробно основные свойства интерференционной картины, создаваемой двумя источниками электромагнитных волн одинаковой интенсивности и наблюдаемой на плоском экране, расположенным на расстоянии
Область, в которой волны источников перекрываются, называется полем интерференции. В поле интерференции имеются места, где волны источников будут складываться в фазе. В этих местах будут отмечаться максимумы интенсивности электромагнитного поля. Там же, где волны будут складываться в противофазе - минимальная интенсивность. Если в поле интерференции поместить непрозрачный экран, то будет наблюдается чередование светлых и тёмных полос (рис. 4.3a), представляющие собой интерференционную картину. Параметрами интерференционной картины являются положение её максимумов
В соответствии с (4.4a) для расчёта этих величин надо найти разность фаз
где
Из рис. 4.3a имеем очевидные соотношения, определяющие расстояния
Отсюда следует, что
Принимая во внимание, что
Использование этого соотношения приводит к следующему выражению для оптической разности хода волн
Максимум интерференционной картины будет наблюдаться при условии синфазного сложения колебаний волн источников, которое имеет место при
где
Найдём координату
где
Порядком интерференционного максимума называют его номер '
Аналогичным образом можно найти положения минимумов интерференционной картины двух источников, определяемые координатами
где
Отсюда следует, что в рассматриваемой интерференционной картине положения соседних интерференционных максимумов и минимумов находятся на одинаковом расстоянии друг от друга и не зависят от того, насколько эти максимумы удалены от центра интерференционной картины. Это свойство максимумов и минимумов позволяет определить ширину интерференционной полосы.
Ширина интерференционной полосы определяется, как расстояние между соседними интерференционными максимумами или минимумами, интерференционные порядки которых отличаются на единицу. Для рассматриваемой интерференционной картины двух источников волн одинаковой интенсивности в соответствии с выражениями (4.9) ширина полосы
Из этой формулы следует, что расстояние между интерференционными полосами растёт при уменьшении
В этом случае для световых волн, длина волны которых
Рассмотрим распределение интенсивности света в плоскости интерференционной картины, если интенсивность источников одинаковы, т.е.
где
В плоскости экрана интенсивность интерференционной картины (рис. 4.3b) двух точечных монохроматических источников электромагнитных волн одинаковой интенсивности
Изменение интенсивности в соответствии с этим выражением в оптике известно, как изменение интенсивности по закону "квадрат косинуса". В максимумах интенсивность интерференционной картины в четыре раза превышает интенсивность интерферирующих источников волны. В минимумах интенсивность равна нулю. Среднее значение распределения интенсивности
Для немонохроматических источников электромагнитных волн в центре картины максимумы всех составляющих колебаний разных частот интерферирующих источников совпадают. Однако, по мере удаления от центра ввиду того, что направления на максимумы и минимумы зависят от длины волны, может происходить ' наложение' интерференционных максимумов одной волны на минимумы другой. В результате
интерференционная картина немонохроматических источников будет смазываться ближе к краю их интерференционного поля. Следовательно, число наблюдаемых интерференционных полос будет меньше по сравнению со случаем монохроматических источников. Возможность наблюдения интерференционной картины электромагнитных волн обусловлена свойством когерентности их источников, подробнее рассматриваемой в следующем параграфе.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 833; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 от плоскости расположения от источников. В качестве таких источников могут мыслиться, например две бесконечно-узкие, параллельные друг - другу щели или два отверстия бесконечно малого диаметра, расстояние между которыми
от плоскости расположения от источников. В качестве таких источников могут мыслиться, например две бесконечно-узкие, параллельные друг - другу щели или два отверстия бесконечно малого диаметра, расстояние между которыми  , прорезанные в плоском непрозрачном экране (рис. 4.3a). Пусть источники электромагнитных волн располагаются в однородной среде с показателем преломления
, прорезанные в плоском непрозрачном экране (рис. 4.3a). Пусть источники электромагнитных волн располагаются в однородной среде с показателем преломления  .
.
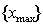 и минимумов
и минимумов 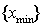 , а также связанная с ними ширина полос интерференционной картины
, а также связанная с ними ширина полос интерференционной картины 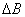 (рис. 4.3a).
(рис. 4.3a). излучаемых источниками волн в точке наблюдения, расположенной на экране. Как показано в главе 3, для расчёта
излучаемых источниками волн в точке наблюдения, расположенной на экране. Как показано в главе 3, для расчёта 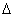 волн от первого и второго источников (рис. 4.3a) до точки наблюдения, поскольку
волн от первого и второго источников (рис. 4.3a) до точки наблюдения, поскольку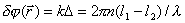 ,
, - расстояния, проходимые волнами соответственно от первого и второго источников (рис. 4.3a) до точки наблюдения;
- расстояния, проходимые волнами соответственно от первого и второго источников (рис. 4.3a) до точки наблюдения; 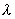 - длина волны.
- длина волны.


 при условии
при условии  .
. .
.
 . Исходя из связи между разностью фаз колебаний и оптической разностью хода
. Исходя из связи между разностью фаз колебаний и оптической разностью хода  , можно заключить, что синфазное сложение колебаний имеет место при условии кратности оптической разности хода целому числу длин волны
, можно заключить, что синфазное сложение колебаний имеет место при условии кратности оптической разности хода целому числу длин волны  ,
,
 - произвольное целое число, равное
- произвольное целое число, равное  .
. , определяющую положение
, определяющую положение 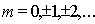 - ого максимума интерференционной картины:
- ого максимума интерференционной картины: ,
,
 - длина волны в вакууме, связанная с длиной волны
- длина волны в вакууме, связанная с длиной волны  в среде распространения с помощью формулы
в среде распространения с помощью формулы  .
.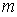 ', отсчитываемый от центрального (
', отсчитываемый от центрального (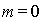 ), которому соответствует центр интерференционной картины, где складываются волны от источников, проходящие одинаковый путь (
), которому соответствует центр интерференционной картины, где складываются волны от источников, проходящие одинаковый путь ( ).
).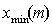 , если положить оптическую разность хода кратной нечётному числу полуволн:
, если положить оптическую разность хода кратной нечётному числу полуволн: .
.
 .
.
 . Кроме того, если расстояние до экрана соизмеримо с расстоянием между щелями (
. Кроме того, если расстояние до экрана соизмеримо с расстоянием между щелями ( ), то
), то .
.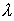 порядка долей микрона, интерференционные полосы неразличимы невооружённым взглядом и для их наблюдения необходимо использовать микроскоп.
порядка долей микрона, интерференционные полосы неразличимы невооружённым взглядом и для их наблюдения необходимо использовать микроскоп. . Из выражения (4.4a) в этом случае следует:
. Из выражения (4.4a) в этом случае следует: ,
,
 - волновое число электромагнитных волн в вакууме,
- волновое число электромагнитных волн в вакууме,  в соответствии с выражением (4.7).
в соответствии с выражением (4.7).
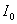 меняется в зависимости от координаты
меняется в зависимости от координаты 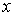 точки наблюдения на экране в соответствии с выражением, следующим из (4.4a)
точки наблюдения на экране в соответствии с выражением, следующим из (4.4a) .
. на интерференционной картине равно сумме интенсивностей каждого из интерферирующих источников. На рис. 4.3c приводится фотография распределения интенсивности интерференционной картины от двух щелей. Полутона, видные на фотографии, соответствуют изменению интенсивности по закону 'квадрат косинуса '.
на интерференционной картине равно сумме интенсивностей каждого из интерферирующих источников. На рис. 4.3c приводится фотография распределения интенсивности интерференционной картины от двух щелей. Полутона, видные на фотографии, соответствуют изменению интенсивности по закону 'квадрат косинуса '.



