
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика материальной точки. Законы ньютона. Импульс тела. Закон сохранения импульса. Центр инерции механической системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Динамика — количественное описание взаимодействия тел, определяющего характер их движения Движение по инерции — движение, происходящее без внешних воздействий.Первый закон Ньютона: тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние Сила — векторная физическая величина, являющаяся мерой взаимодействия тела с другими телами, в результате которого тело приобретает ускорение (или изменяет свою форму и размеры) Единица силы — ньютон (Н).
Инертность — физическое свойство тела в отсутствие трения оказывать сопротивление изменению его скорости Масса (инертная масса) — физическая величина, характеризующая меру инертности тела Единица массы — килограмм (кг) Принцип суперпозиции сил: результирующая сила, действующая на частицу со стороны других тел, равна векторной сумме сил, с которыми каждое из этих тел действует на частицу.
Второй закон Ньютона: в инерциальной системе отсчета ускорение тела прямо пропорционально векторной сумме всех действующих на него сил и обратно пропорционально массе тела Третий закон Ньютона: силы, с которыми два тела действуют друг на друга, равны по величине, противоположны по направлению и приложены к разным телам:
Закон Гука: сила упругости, возникающая при деформации тела, прямо пропорциональна его удлинению и направлена противоположно направлению деформации.
Сила трения — сила, препятствующая относительному перемещению соприкасающихся тел, направленная вдоль поверхности их контакта. Сила трения покоя равна по величине и противоположно направлена силе, приложенной к покоящемуся телу параллельно поверхности его контакта с другим телом. Максимальная сила трения покоя пропорциональна силе реакции опоры:
где μ — коэффициент трения скольжения. Сила трения качения
где μкач — коэффициент трения качения (μкач << μ <μп). Закон всемирного тяготения: гравитационная сила притяжения материальных точек пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
где G = 6,67 • 10-11 Н • м2/кг2 - гравитационная постоянная Сила тяжести — гравитационная сила, действующая на тело Вблизи поверхности Земли сила тяжести, действующая на тело массой m,
В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:
соответственно величина Если мы имеем дело с телом конечного размера, не состоящим из дискретных материальных точек, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками и просуммировать по ним, в результате получим:
Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:
Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*). В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина
где mi — масса i-й материальной точки. Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта. Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как
На практике часто применяются следующие соотношения между массой, импульсом и энергией частицы:
В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.Закон сохранения импульса — Векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия
Докажем закон сохранения импульса. Возьмем и обозначим массы двух тел По третьему закон Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить
Для изменений импульсов тел при их взаимодействии на основании Импульса силы можно записать так Для первого тела:
Для второго тела:
И тогда у нас получается, что закон сохранения импульсов выглядит так:
Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, или равны нулю, сумма импульсов тел остается неизменной. Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета.Систе́маце́нтра масс (систе́маце́нтраине́рции) — невращающаяся система отсчёта, связанная с центром масс механической системы. Обычно сокращается как с. ц. м. или с. ц. и. Суммарный импульс системы вс.ц.м. равен нулю. Для замкнутой системы её система центра масс инерциальна, тогда как незамкнутая система в общем случае может обладать неинерциальной системой центра масс. Суммарная кинетическая энергия механической системы в с.ц.м. минимальна среди всех систем отсчёта; в любой другой невращающейся (необязательно инерциальной) системе отсчёта кинетическая энергия равна кинетической энергии в с.ц.м. плюс кинетическая энергия движения механической системы как целого (MV²/2, где М — полная масса механической системы, V — относительная скорость движения систем отсчёта). При рассмотрении задач рассеяния частиц термин «система центра масс» употребляется как антоним термина «лабораторная система отсчёта». Если экспериментальные исследования проводятся в лабораторной системе, то есть в системе, связанной с наблюдателем (неподвижным относительно частицы-мишени), то теоретическое рассмотрение задач рассеяния удобно проводить в движущейся относительно мишени системе центра масс. При переходе от лабораторной системы в систему центра масс меняются определения углов рассеяния частиц, так что для сравнения теории с экспериментом необходимо проводить перерасчёт полученных сечений рассеяния. Например, при изучении столкновения двух одинаковых частиц, одна из частиц (мишень) до столкновения остается неподвижной, вторая налетает с некоторой конечной скоростью. При упругом лобовом столкновении вторая частица останавливается, передавая всю свою кинетическую энергию и импульс первой частице. Такая картина наблюдается в лабораторной системе отсчета. С точки зрения системы центра масс, частицы движутся навстречу друг другу с одинаковыми скоростями и после столкновения разлетаются в обе стороны с теми же (с точностью до знака) скоростями. В нерелятивистском пределе координаты центра масс системы из n частиц, имеющих массы
(М — масса всей системы тел). Продифференцировав по времени, получим скорость движения центра масс
(
В релятивистском случае центр масс не является лоренц-инвариантом, однако система центра масс определяется и играет важную роль в релятивистской кинематике. Систему центра масс в релятивистском случае следует определять как систему отсчёта, в которой сумма импульсов всех тел системы равна нулю.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.008 с.) |

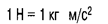
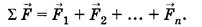
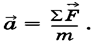
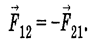 Все механические явления определяются электромагнитным и гравитационным взаимодействиями Электромагнитными силами являются сила упругости и сила трения. Упругое воздействие на тело — воздействие, в результате которого тело восстанавливает форму и размеры.
Все механические явления определяются электромагнитным и гравитационным взаимодействиями Электромагнитными силами являются сила упругости и сила трения. Упругое воздействие на тело — воздействие, в результате которого тело восстанавливает форму и размеры.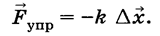 Сила реакции опоры — сила, действующая на тело со стороны опоры перпендикулярно ее поверхности Сила натяжения — сила упругости, действующая на тело со стороны нити или пружины
Сила реакции опоры — сила, действующая на тело со стороны опоры перпендикулярно ее поверхности Сила натяжения — сила упругости, действующая на тело со стороны нити или пружины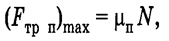 где μп — коэффициент трения покоя. Сила трения скольжения
где μп — коэффициент трения покоя. Сила трения скольжения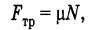
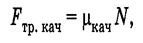
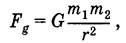
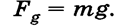 И́мпульс (Коли́честводвиже́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
И́мпульс (Коли́честводвиже́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости: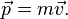
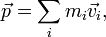
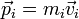 называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).
называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).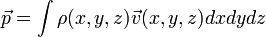
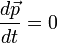 . (*)
. (*) ,
,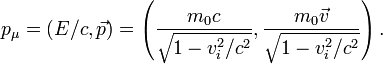
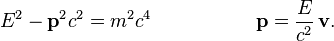



 и
и  и скорости до взаимодействия
и скорости до взаимодействия  , а после взаимодействия (столкновения)
, а после взаимодействия (столкновения) 



 и (в некоторой системе отсчёта К) радиус-векторы
и (в некоторой системе отсчёта К) радиус-векторы  :
:

 — импульсы частиц), которую можно использовать для перехода от данной системы отсчёта Кк системе центра масс, вычисляя скорости и радиус-векторы частиц в ней по формулам:
— импульсы частиц), которую можно использовать для перехода от данной системы отсчёта Кк системе центра масс, вычисляя скорости и радиус-векторы частиц в ней по формулам:




