
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И1.Законы геометрической оптики.Их обоснование с точки зрения теории Гюйгенса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И1.Законы геометрической оптики.Их обоснование с точки зрения теории Гюйгенса. Oптика – наука о природе света и явлений, связанных с распространением и взаимодействием света. Впервые оптика, была сформулирована в сер.17в.Ньютоном и Гюйгенсом. Ими были сформулированы законы геометрической оптики:1). Закон прямолинейного распространения света – свет распространяется в виде лучей, доказательством чего является образование резкой тени на экране, если на пути световых лучей находится непрозрачная преграда. Доказательством является и образование полутени.
4).синус угла падения относится к синусу угла отражения относятся
Первый закон Ньютон обьяснил из сох Ранения импульса 2-ой з-н динамики, а Гюйгенс не смог его объяснить. t 2-ой закон:Гюйгенс:две несогласованные волны не возмущают друг друга Ньютон: не смог: столкновение частиц – возмущение. 3-ий з-н:Ньютон: объяснил как и з-н сохранения импульса
В 19 веке появляются ряд работ:Френеля, Юнга, которые док-ют, что свет это волна.В сер.19 века была создана теория электромагнитное поле Максвела, согласно теории, что эти волны являются поперечными и только свет волны испытывает на себе явление поляризации. Полное внутреннее отражение.
Линзы. Вывод формулы линзы. Построение изображений в линзе. Линзы Линза представляет собой обычно стеклянное тело, ограниченное с двух сторон сферическими поверхностями; в частном случае одна из поверхностей линзы может быть плоскостью, которую можно рассматривать как сферическую поверхность бесконечно большого радиуса. Линзы могут быть изготовлены не только из стекла, но и из любого прозрачного вещества (кварц, каменная соль и тд.). Поверхности линз могут быть также более сложной формы, например цилиндрические, параболические. Точка О оптический центр линзы. О1О2 толщина линзы. С1 и С2 – центры ограничивающих линзу сферических поверхностей. Всякая прямая проходящая через оптический центр называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей линзы наз. главной оптической осью. Остальные – побочными осями. Вывод формулы линзы
EG=KA+AO+OB+BL;KA=h2/S1; BL= h2/S2; EG=h2/r1+h2/r2+ h2/S1+ h2/S2=U1/U2; U1=c/n1; U2=c/n2 (h2/r1+h2/r2)=1/S1+1/r1+1/S2+1/r2=n2/n1(1/r1+1/r2); 1/S1+1/S2=(n2/n1-1)(1/r1+1/r2); 1/d+1/f=1/F=(n2/n1-1)(1/r1+1/r2); r1,r2>0 -выпуклая r1,r2<0 – вогнутая d=x1+F; f =x2+F;x1x2=F2; Построение изображений в линзе
Просветление оптики. Интерференция при отражении от тонких пленок лежит в основе просветления оптики. Прохождение света через каждую преломляющую поверхность линзы сопровождается отражением примерно 4% падающего света. В сложных объективах такие отражения совершаются многократно и суммарная потеря светового потока достигает заметной величины. Кроме того, отражения от поверхностей линз приводят к возникновению бликов. В просветленной оптике для устранении отражения света на каждую свободную поверхность линзы наносится тонкая пленка вещества с показателем преломления иным, чем у линзы. Толщина пленки подбирается так, чтобы волны, отраженные от обеих ее поверхностей, погашали друг друга. Особенно хороший результат достигается в том случае, если показатель преломления пленки равен корню квадратному из показателя преломления линзы. При этом условии интенсивность обеих отраженных от поверхностей пленки волн одинакова. Применение интерференции. Явление интерференции применяется для обнаружения дефектов либо для определения показателя преломления с очень высокой точностью. Для этих целей применяются интерферометры. Бизеркало Френеля Свет от точечного источника S падает на два плоских зеркала m1C m2C расположенных перпендикулярно плоскости рисунка и соединенных по линии С. Угол между плоскостями зеркал очень мал. Свет от источника S распространяется после отражения от зеркал в виде двух пучков с центрами в точках S1 и S2 являющихся мнимыми изображениями источника S в зеркалах. Эти пучки когерентны и при наложении дают на экране интерференционную картину (область ВС, называемая полем интерференции). Результат интерференции в некоторой точке О экрана зависит от длины волны света λ и разности хода волн от когерентных мнимых источников S1 S2 до точки M:
Расчет интерференционной картины
l=a+b; d=S’S’’=2bφ
CO=a; SC=b=S’C=S’’C
Фазовые пластинки Пластинки, вырезанные вдоль оптической оси видимого луча, преломление не наблюдается, однако в пластинке распространяются два фронта волн, между которыми на выходе из пластинки между ними появляется оптическая разность хода Если Закон Малюса. Допустим, что два поляризатора поставлены другь за другом, так что их оси ОА1 и ОА2 образуют между сабой некоторый угол. Первый поляризатор пропустит свет, электрический вектор Е0 которого параллелен его оси ОА1. Обозначим через I0 интенсивность этого света. Разложим Е0 на вектор Е//, параллельный оси ОА2
второго поляроида, и вектор 23. Искусственное двойное лучепреломление. Эффект Керра. Оптический метод определения напряжений в образце. Двойное лучепреломление – явление преломления света на границе двух сред. Искусственное двойное лучепреломление - при прохождении из изотропной среды в анизотропную, при этом распространяется два луча. Изотропные вещества в некоторых ситуациях могут вести себя подобно анизотропным. Керр (1875) показал, что при помещении изотропных диэлектриков в электрическое поле, они становятся анизотропными (оптическая ось совпадает с направлением электрического поля). Рассм. Эффект Керра. В установку для получения поляризованного света между поляризатором и анализатором, установленными на темноту (скрещенными), помещается ячейка Керра. Она представляет собой сосуд с прозрачными плоскопараллельными стенками, заполненный активным веществом, чаще всего это бензол, с помещенными в нее электродами, на которые подается напряжение. Между ними проходит луч света. Без поля жидкость изотропна, лучи света не меняют поляризации и поле зрения темное. С появлением электрического поля наблюдается просветление на экране, что доказывает возникновение двойного лучепреломления, т.е. среда стала анизотропной. Бензол ведет себя подобно пластинке, вырезанной вдоль оптической оси. Установлено, что на величину Искусственное двойное лучепреломление может наблюдаться при механических деформациях. Поляризатор и анализатор устанавливается на пути света так, что угол между осями
Данный метод используется для исследования напряжений в строительных конструкциях. Если вещество имеет толщину Областям в теле, имеющим одинаковое напряжение, соответствует одинаковый сдвиг фаз
Эффект Доплера в оптике. Согласно принципу относительности Эйнштейна, уравнение световой волны во всех инерциальных системах отсчёта одинаково по форме. Используя преобразования Лоренца, можно получить уравнение волны, посылаемой источником, в направлении приёмника, в другой инерциальной системе отсчёта, а следовательно и связать частоты световых волн, излучаемых источником (n0) и воспринимаемых источником (n). Теория относительности приводит уравнение описывающее эффект Доплера для электромагнитных волн в вакууме:
При θ=0,
Изменение частоты зависит от
В призменный спектрограф, с помощью которого определяется частота света, направлялись лучи, многократно отражённые от двух параллельных зеркал, перемещающихся по отношению к неподвижному источнику света. S- источник света, находящийся посередине между зеркалами BB1 и CC1, P- коллиматор призменного спектрографа, в который попадают лучи после n- кратного отражения. Определим скорость, с которой перемещается мнимый источник света n кратно отраженных лучей в результате перемещения зеркал со скоростью v. Для этого определим местоположение мнимого источника света n-кратных отраженных лучей. Луч SA отражается от зеркала BB1 так, как если бы он выходил из мнимого источника света S1 отражается от зеркала на таком же расстоянии a как и действительный источник. Луч, испытывающий n отражений в этих параллельных зеркалах и попадающий в коллиматор призменного спектрографа P, распространяется так, как будто он вышел из мнимого источника, отстающего от зеркала на расстоянии: Поэтому если привести зеркала BB1 и CC1 по отношению к источнику света в движение со скоростью Тепловое излучение. Тепловым излучением называется излучение нагретых тел. Все тела обладают тепловым излучением. Основная особенность теплового излучения – равновесность (тепловое излучение – это единственное равновесное излучение). Это означает, что количество излученной энергии и количество поглощенной в замкнутой системе равны.все остальные виды излучений наз. люминисценциями. Тепловое излучение – это электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и оптических свойств этого тела Основные характеристики. Энергетическая светимость Спектральная плотность энергетической светимости. Энергетическая светимость – это количество энергии испускаемой с единицы площади за единицу времени. R(T)=d2W/(dSdT);(Вт/м2) Спектральная плотность энергетической светимости – это количество тепловой энер r(λ,T)=d2W/(dSdtdλ)=dR/dλ (Вт/м2м) R= Закон Кирхгофа: отношение спектральной плотности энергетической светимости к поглащательной способности при данной длине волны и температуре есть универсальная функция. r(λ,T)arT= r(λ,T)/ a(λ,T)
Закон Стефана – Больцмана: энергетическая светимость черного тела пропорциональна четвертой степени его термодинаической температуры R0э=σT4 Закон Вина: частота, соответствующая максимальному значению энергетической светимости черного тела, прямо пропорциональна его термодинамической температуре. b1=
Абсолютно черное тело – это тело, если оно при любой температуре полностью поглощает всю энергию падающих на него электромагнитных волн независимо от их частоты, поляризации и направления распространения.
Модель а.ч.т. – это полость с отверстием больших размеров произвольной формы с теплоизолированными стенками и зеркальной внутренней поверхностью. Отверстие является а.ч.т. Свет попадает в отверстие, многократно отражаясь внутри полости. Вероятность выхода луча 30. Излучение черного тела. Формулы Релея-Джинса, Вина, Планка для теплов. излучения черног о тела. Вывод формулы Планка. Тело называется абсолютно черным (абс.ч.т.), если его поглощательная способность
Ф-ла Релея-Джинса: Ф-лы Вина: 1) Ф-ла Планка: Вывод ф-лы Планка. Он исходил из того, что т.к. тепловое излучение равновесно, то в любой момент времени, достаточно большой по сравнению с атомными временами (
1 переход - вынужденное поглощение. Вероятность этого перехода 2 переход - вынужденное издучение. Вероятность:
1) Пусть 2) 31. Вывод законов теплового излучения (законов Вина, Стефана-Больцмана) из формулы Планка. Закон Вина и закон Стефана-Больцмана являются следствием формулы Планка. Согласно формуле Планка, интегральная плотность энергии равновесного излучения в вакууме равна:
Разложив знаменатель
где  - некоторая функция произведения - некоторая функция произведения 
Выражение в квадратных скобках представляет некоторую функцию При длине волны Продифференцируем формулу Планка:
Обозначив
Интерференция фотонов. Описываются интерференционные опыты при малых интенсивностях светового потока, из которых делается вывод о существовании явления интерференции при наличии лишь одного фотона. Обсуждается интерпретация явлений интерференции в рамках корпускулярных представлений. 1) Если световой поток представить как поток фотонов, то необходимо допустить, что концентрация фотонов в потоке пропорционально квадрату амплитуды напряжённости электрического поля волны ( 2) Нельзя представить интерференцию как процесс «суперпозиции фотонов». При использовании представления о фотонах образования центров проявления объясняется поглощения фотонов частицами галоидного серебра. Частица галоидного серебра равномерно распределяются по объёму само чувствительного слоя. Вероятность поглощения фотона галоидной частицей для фотонов фиксированной частоты может считаться постоянной. Число поглощённых фотонов в некотором физически бесконечно малом объёме пропорционально произведению числа частиц галоидного серебра в этом объёме, вероятности поглощения фотона и концентрации фотонов. «Почернения» объёма, с одной стороны, пропорционально числу поглощённых фотонов, а с другой стороны интенсивности интерференционной картины. Отсюда заключаем, что концентрация фотонов в стоячей волне пропорционально Поглащения фотона частицей галоидного серебра обозначает физическое обнаружения фотона в области этой частицей. Поглащения фотона галоидной частицей является случайным процессом и может описываться лишь вероятносными методами. Изложенные рассуждения позволяют сделать заключение, что плотность вероятности обнаружить фотон вблизи координаты z пропорциональна квадрату амплитуды напряжённости электрического поля волны. Этот вывод важен для корпускулярной интерпритации интерференции электромагннитных волн, но не означает, что фотон обладает координатами и движется по какой-то траиктории. Фотоэффект. Фотоэффект был открыт Герцем в 1887. Изучен был Столетовым. Явление вырывания электронов с поверхности металлов под действием света получило название фотоэффекта. Экспериментальные з-ны фотоэффекта. 1.Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности. 2.Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота 3.Число фотоэлектронов n, вырываемых из анода за единицу времени, пропорционально интенсивности света (фототок насыщения пропорционален энергетической освещенности катода). Чем определяется числовое значение граничной частоты?
Она зависит только от работы выхода электрона, т.е. от химической природы металла и состояния его поверхности. Почему максимальная энергия фотоэлектронов не зависит от плотности потока энергии падающего излучения? Почему в явлении фотоэффекта существование пороговой частоты говорит в пользу фотонной теории и против волновой? Кинетическая энергия, с которой вырывается электрон из металла, должна была бы зависеть от интенсивности падающего света, так как с увеличением последней электрону бы передавалась бы большая энергия. однако этот вывод противоречит 2 з-ну фотоэффекта. Так, как по волновой теории, энергия, передаваемая электронам, пропорциональна интенсивности света, то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла: иными словами, красной границы фотоэффекта не должно быть, что противоречит 3 з-ну фотоэффекта. Кроме того, волновая теория не смогла объяснить безинерционность фотоэффекта, установленную опытами. Таким образом, фотоэффект необъясним с точки зрения волновой теории света.
Эффект Комптона.
Гамма фотон рассеивается на электрон и электрон приобретает импульс и в результате рассеянный Согласно закону сохранения импульса: Длина волны рассеиваемого излучения зависит от частоты падающего света.
Следствие: Т.к. Квантовомеханическая теория атома водорода. Собственное значения и собственные функции для стационарных состояний атома водорода. Орбитальный момент электрона по квантовой теории. Гиромагнитное отношение. Атом водорода – простейшая система для которой были получены точные решения уравнений квантовой механики. Уравнение Шредингера Поскольку потенциальная энергия сферически симметрична, то оператор Лапласа в уравнении Шредингера лучше взять в сферических координатах. По этой причине Уравнение Шредингера в следствии сферической симметрии разлаживается на 3 уравнения, каждое из которых зависит только от одной переменной. На она должна быть однозначной должна быть непрерывной должна быть конечной. Так как Так как энергия сферически симметрична, а также из условия однозначности волновой функции следует, что функции Функция Функции должны быть непрерывными, однозначными и конечными исходя из физического смысла – а именно вероятность не может быть >1 или бесконечной. Угловая функция зависит от l m, и при решении уравнения Шредингера она определяет момент импульса Решение радиального уравнения приводит к специальной функции – полином Лагерра и квадрат этой функции определяет вероятность обнаружения электрона на определенном расстоянии от ядра.
Имеется соответствие атом водорода в квантовой механике решается абсолютно точно квантовые числа n, l и m получаются как следствия решения этого уравнения. В то же время результаты квантовой механики и результаты Бора совпадают, а именно: уравнение Шредингера дает максимум вероятности на боровских орбитах. Гиромагнитное отношение – отношение модуля магнитного момента в единицах
Спектры щелочных элементов. Щелочные металлы одновалентны и их сравнительно легко ионизировать. Если атом щелочного металла имеет всего z электронов, то можно утверждать, что z-1 электронов образуют структуру атома благородного атома, а последний электрон связан с этими электронами и ядром весьма слабо. Таким образом, первые z-1 электронов и ядро образуют остов с зарядом +e, в эффективном поле которого движется электрон, называемый валентным. Таким образом, щелочные атомы являются водородоподобными атомами, однако не полностью. Дело в том, что внешний электрон несколько деформирует оболочку первых z-1 электронов и несколько искажает их поле. Поэтому потенциальную энергию валентного электрона можно представить в виде Зависимость энергии от орбитального квантового числа составляет принципиальное отличие уровней энергии атомов щелочных металлов от уровней энергии атома водорода. Схему уровней энергии атомов щелочных металлов нельзя представить в функции лишь одного главного квантового числа: уровни энергии, соответствующие одному и тому же квантовому числу, но с различными орбитальными числами, не совп
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 935; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.251.204 (0.011 с.) |



 2).закон независимости световых пучков – если световые потоки от двух независимых
2).закон независимости световых пучков – если световые потоки от двух независимых источников пересекаются, они друг друга не возмущают.
источников пересекаются, они друг друга не возмущают.

 также как показатели отношения преломления двух сред.
также как показатели отношения преломления двух сред. 
 Принцип Гюйгенса:если свет – это волна, то от источника света распространяется волновой фронт, а каждая точка волнового фронта в данный момент времени являются источником вторичных волн, огибающая вторичных волн представляет новый фронт волн.
Принцип Гюйгенса:если свет – это волна, то от источника света распространяется волновой фронт, а каждая точка волнового фронта в данный момент времени являются источником вторичных волн, огибающая вторичных волн представляет новый фронт волн.



 4-ый з-н.
4-ый з-н. af-фронт пеломлённой волны.
af-фронт пеломлённой волны.




 ;
;  ;
;  ;
;  ;
;
 Начальные фазы колебания источников S1 S2 одинаковы, поэтому условия интерференционных максимумов и минимов имеют вид:
Начальные фазы колебания источников S1 S2 одинаковы, поэтому условия интерференционных максимумов и минимов имеют вид:  максимум m-го порядка
максимум m-го порядка минимум m-го порядка
минимум m-го порядка
 ; AB=2aφ (длина хорды);
; AB=2aφ (длина хорды);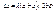

 .
. - пластинка называется в ¼ длины волны,
- пластинка называется в ¼ длины волны,  - в половину длины волны.
- в половину длины волны.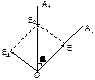
 , перпендикулярный к ней составляющая
, перпендикулярный к ней составляющая  , длина которого
, длина которого  . Интенсивность света, прошедшего через оба поляризатора,будет
. Интенсивность света, прошедшего через оба поляризатора,будет  . Такое соотношение справедливо для любого полиризатора и анализатора. Оно называется законом Малюса.
. Такое соотношение справедливо для любого полиризатора и анализатора. Оно называется законом Малюса. (степень анизотропии) влияет напряженность электрического поля и величина длины волны лучей:
(степень анизотропии) влияет напряженность электрического поля и величина длины волны лучей: 
 -постоянная ячейки Керра. Ячейка Керра применяется для быстрого модулирования интенсивности света (киносъемка), В электронике используется как быстро действующий затвор (
-постоянная ячейки Керра. Ячейка Керра применяется для быстрого модулирования интенсивности света (киносъемка), В электронике используется как быстро действующий затвор (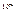 с), в схемах для создания обратной связи в резонаторах. Ячейка Покильса – магнитное поле.
с), в схемах для создания обратной связи в резонаторах. Ячейка Покильса – магнитное поле. , они скрещены, установлены на темноту. Между ними помещается изотропное вещество (орг.стекло), при этом ничего не изменяется. Затем прикладываем усилие, например, в одних направлениях образец сжимаем, а в других – растягиваем, при этом условия распространения света по различным направлениям окажутся различными и изотропная пластинка окажется анизотропной.
, они скрещены, установлены на темноту. Между ними помещается изотропное вещество (орг.стекло), при этом ничего не изменяется. Затем прикладываем усилие, например, в одних направлениях образец сжимаем, а в других – растягиваем, при этом условия распространения света по различным направлениям окажутся различными и изотропная пластинка окажется анизотропной.  - напряжение в образце
- напряжение в образце

 , то разность фаз, возникающая при прохождении обыкновенного и необыкновенного лучей через этот слой равна
, то разность фаз, возникающая при прохождении обыкновенного и необыкновенного лучей через этот слой равна 
 и одинаковая окраска, т.е линии одинаковой окраски являются линиями равного напряженного состояния. Наблюдая с помощью анализатора прохождение поляризованного света через тело, можно по окраске судить о характере распределения напряжений в образце. Можно также вычислить и численное значение величины напряжения, но это сложно и чаще ограничиваются картиной распределения напряжений. Данный метод применяется к телам любой формы.
и одинаковая окраска, т.е линии одинаковой окраски являются линиями равного напряженного состояния. Наблюдая с помощью анализатора прохождение поляризованного света через тело, можно по окраске судить о характере распределения напряжений в образце. Можно также вычислить и численное значение величины напряжения, но это сложно и чаще ограничиваются картиной распределения напряжений. Данный метод применяется к телам любой формы. , где v- скорость источника света относительно приёмника, с- скорость света в вакууме.
, где v- скорость источника света относительно приёмника, с- скорость света в вакууме.  , θ - угол между вектором скорости v и направлением наблюдения, измеряемый в системе отсчёта связанной с наблюдением.
, θ - угол между вектором скорости v и направлением наблюдения, измеряемый в системе отсчёта связанной с наблюдением. продольный эффект Доплера, наблюдаемый при движении приёмника вдоль линии, соединяющей его с источником. При малых около светных скоростях v(v<<c), разлагая в ряд и пренебрегая числом порядка β2, получим:
продольный эффект Доплера, наблюдаемый при движении приёмника вдоль линии, соединяющей его с источником. При малых около светных скоростях v(v<<c), разлагая в ряд и пренебрегая числом порядка β2, получим:
 , но для заметного. По величине смещения необходимо перемещать источник света относительно приёмника с большой скоростью.
, но для заметного. По величине смещения необходимо перемещать источник света относительно приёмника с большой скоростью.
 . При изменении расстояния a на (a+Δa), мнимый источник переместится и будет отстоять на расстоянии b+Δb=(2n-1)(d+Δd) но так как само зеркало переместилось на расстояние Δa то по отношению к неподвижным телам источник переместится на расстояние Δb’=Δb-Δa=2(n-1)Δa
. При изменении расстояния a на (a+Δa), мнимый источник переместится и будет отстоять на расстоянии b+Δb=(2n-1)(d+Δd) но так как само зеркало переместилось на расстояние Δa то по отношению к неподвижным телам источник переместится на расстояние Δb’=Δb-Δa=2(n-1)Δa , но мнимый источник света сответственный n простым отражённым лучам, будет перемещаться по отношению к спектрографу, с помощью которого измеряется длина волны световых лучей со скоростью
, но мнимый источник света сответственный n простым отражённым лучам, будет перемещаться по отношению к спектрографу, с помощью которого измеряется длина волны световых лучей со скоростью  ,которая в 2(n-1) раз превышает скорость действительного перемещения зеркал.
,которая в 2(n-1) раз превышает скорость действительного перемещения зеркал. гии испускаемой с единичной поверхности в единицу времени в интервале частот от
гии испускаемой с единичной поверхности в единицу времени в интервале частот от 
 m /T, где b1 - постоянная величина.
m /T, где b1 - постоянная величина.
 0.Отверстие излучает энергию в виде тепла.
0.Отверстие излучает энергию в виде тепла. для излучения всех частот. Тогда,
для излучения всех частот. Тогда,  . Поэтому равновесное излучение наз. также черным излучением. Т.к.
. Поэтому равновесное излучение наз. также черным излучением. Т.к.  , а равновесное излучение изотропно, то излучательная способность абс.ч.т. одинаково по всем направлениям. Распределение энергии в спектре абс.ч.т.(рис.1).
, а равновесное излучение изотропно, то излучательная способность абс.ч.т. одинаково по всем направлениям. Распределение энергии в спектре абс.ч.т.(рис.1).
 .
. , где
, где  . 2)
. 2) 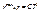 , где
, где 
 .
. .
. ) число атомов испускания должно быть = числу атомов поглощения. Первоначально теорию излучения создал Эйнштейн. Она заключается в след.: атом излуч. и поглощает только, если переходит с одного энергетического уровня на другой.(рис.)
) число атомов испускания должно быть = числу атомов поглощения. Первоначально теорию излучения создал Эйнштейн. Она заключается в след.: атом излуч. и поглощает только, если переходит с одного энергетического уровня на другой.(рис.)

 - коэффиц. поглощения Эйнштейна. Интенсивность поглощения:
- коэффиц. поглощения Эйнштейна. Интенсивность поглощения:  , где
, где  -заселенность энерг.ур 1,
-заселенность энерг.ур 1,  -плотность светового потока. Переход со 2 на 1ур.-спонтанное излучение. Вероятность:
-плотность светового потока. Переход со 2 на 1ур.-спонтанное излучение. Вероятность:  . Интенсивность излучения:
. Интенсивность излучения:  .
. . Интенсивность:
. Интенсивность:  . Вынужденный фотон абсолютно когерентен.
. Вынужденный фотон абсолютно когерентен. - условие равновесия.
- условие равновесия.
 .
.
 .
.
 Следовательно,
Следовательно,  . - ф-ла Планка.
. - ф-ла Планка.
 ,
,  .
. в ряд и интегрируя, получим для последнего интеграла:
в ряд и интегрируя, получим для последнего интеграла: , отсюда:
, отсюда:  .
.
 - закон Стефана-Больцмана.
- закон Стефана-Больцмана. , F – некоторая функция отношения частоты к температуре.
, F – некоторая функция отношения частоты к температуре.

 .
. , соответствующей максимуму функции
, соответствующей максимуму функции  , выражение должно обращаться в нуль:
, выражение должно обращаться в нуль: 



 .
. получим:
получим: 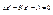

 , откуда
, откуда  - закон Вина.
- закон Вина.
 ).
). , т. е. изменяется на длине стоячей волны и определяется квадратом амплитуды колебаний вектора напряжённости электрического поля в соответствующих точках стоячей волны.
, т. е. изменяется на длине стоячей волны и определяется квадратом амплитуды колебаний вектора напряжённости электрического поля в соответствующих точках стоячей волны. , при которой еще возможен фотоэффект (
, при которой еще возможен фотоэффект ( , где А – работа выхода, h – постоянная Планка.
, где А – работа выхода, h – постоянная Планка.

 ;
; 
 ;
; 


 имеет
имеет  м, то становится понятным, почему эффект Комптона на рентгене и
м, то становится понятным, почему эффект Комптона на рентгене и  м и величину
м и величину  м может наблюдаться в видимом свете.
м может наблюдаться в видимом свете. , где
, где  ,
,  - волновая функция. В сферических координатах
- волновая функция. В сферических координатах  . Решить уравнение Шредингера это значит найти собственные значения энергии
. Решить уравнение Шредингера это значит найти собственные значения энергии  и собственные функции
и собственные функции  . Все уравнения отличаются только значением
. Все уравнения отличаются только значением  .
.  - для атома водорода и водородоподобных систем.
- для атома водорода и водородоподобных систем. , где
, где  .
. , где
, где  - радиальная функция,
- радиальная функция,  - угловая функция,
- угловая функция,  .
. - квадрат определяет вероятность найти данную частицу в единице объема с коэффициентами x, y, z. Т. е. Квадрат этой функции – плотность вероятности. Исходя из физического смысла
- квадрат определяет вероятность найти данную частицу в единице объема с коэффициентами x, y, z. Т. е. Квадрат этой функции – плотность вероятности. Исходя из физического смысла  , т. к. это достоверное событие и это уравнение называется уравнением нормировки.
, т. к. это достоверное событие и это уравнение называется уравнением нормировки. являются функциями целочисленного аргумента m который может принимать значения
являются функциями целочисленного аргумента m который может принимать значения  и так далее.
и так далее. непрерывная и однозначная является спец. Функцией – присоединенные функции Лежандра. Они имеют однозначные и конечные решения только при целочисленных значениях l, которые иногда могут быть отрицательными и связано с m: m=-l,…,0,…l.
непрерывная и однозначная является спец. Функцией – присоединенные функции Лежандра. Они имеют однозначные и конечные решения только при целочисленных значениях l, которые иногда могут быть отрицательными и связано с m: m=-l,…,0,…l. и проекцию момента импульса на выделенное направление
и проекцию момента импульса на выделенное направление  , а с точки зрения графического решения она определяет форму электронного облака и его ориентацию.
, а с точки зрения графического решения она определяет форму электронного облака и его ориентацию. , где z – порядковый номер элемента,
, где z – порядковый номер элемента,  - полином Лагерра,
- полином Лагерра,  - боровский первый радиус
- боровский первый радиус  .
. , иначе
, иначе  , где
, где  - безразмерное число гиромагнитное отношение – характеризует соотношение между магнитным и механическим моментами системы.
- безразмерное число гиромагнитное отношение – характеризует соотношение между магнитным и механическим моментами системы. где
где  ,
,  - поправки, учитывающие отличие поля атомов щелочных металлов от поля атома водорода. Можно показать, что энергия зависит не только от квантового числа n, но и от орбитального квантового числа l.
- поправки, учитывающие отличие поля атомов щелочных металлов от поля атома водорода. Можно показать, что энергия зависит не только от квантового числа n, но и от орбитального квантового числа l.


