
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция на одной щели. Как влияет на дифракцию фраунгофера от одной щели увеличение длины волны и ширины щели.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Бесконечно длинную щель можно образовать, расположив рядом две обращённые в разные стороны полуплоскости.Следовательно, задача о дифракции Френеля от щели может быть решена с помощью спирали Корню.Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу.(рис1)
Для точки P, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точки спирали. (рис2)
Если сместиться в точку Френелевская дифракционная картина от щели представляет собой светлую(р.1) или тёмную(р.2) центральную полосу, по обе стороны которой распологаются симметричные относительно неё чередующиеся тёмные и светлые полосы.При большой ширине щели начало и конец результирующего вектора для точки Р лежат на внутренних витках спирали вблизи полюсов Как показывает формула
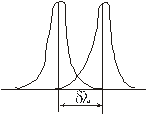
Наоборот, при увеличении ширины щели положен8520/ие первых минимумов придвигается всё ближе и ближе к центру картины, так что центральный максимум становится всё резче и резче.При этом, относительная интенсивность максимума остаётся неизменной; абсолютная же величина его возрастает, ибо возрастает энергия, проходящая через уширенную щель. При очень широкой щели(по сравнению с 14. Дифракционная решётка. Дисперсия и разрешающая сила дифракционной решётки. Укажите порядки главных максимумов, которые не могут наблюдаться на на дифракционной решётке с периодом d=9мкм и шириной одной щели b=3мкм. Дифракционная решётка (одномерная) представляет собой систему параллельных щелей равной ширины, лежащих в одной плоскости и разделённых равными по ширине непрозрачными промежутками. Дифракция, наблюдаемая при прохождении света через такой спектральный прибор, имеет большое практическое значение. Величина d=a+b называется периодом решётки или её постоянной. Разность хода лучей от 2-х соседних щелей будет Дифракционная картина на решётке определяется как результат взаимной интерференции волн, идущих от всех щелей. Поэтому в тех направлениях, в которых ни одна из щелей не распространяет свет, будут наблюдаться главные минимумы, определяемые условием:
Выражение К тому же в направлениях, задаваемых условием: (m=1,2,3,…,N-1,N+1,…,2N-1,2N+1,… мы получим дополнительные минимумы. Для решётки из N щелей между 2-мя главными максимумами находится N-1 щелей, разделённых вторичными максимумами, создающими очень слабый фон. Т. о. чем больше щелей, тем больше образуется минимумов между главными максимумами, и тем более интенсивными и острыми будут сами максимумы.
Основными характеристиками дифракционной решётки являются дисперсия и разрешающая сила.
Дисперсия решётки бывает угловая и линейная. Угловая дисперсия определяет на какой угол расходятся лучи, длины волн которых отличаются на 1Ангстрем.
Линейная дисперсия: Разрешающая способность:
Растояние условию Рэлея, т.е. минимум одного горба должен приходиться на максимум другого. Вывод разрешающей способности решётки: Условия максимумов m-го порядка для лучей 1 и 2 будут
По условию Рэлея
Для дифракционной решётки интенсивность главных максимумов будет выражаться следующим образом:
Т.к. при заданных d и b отношение d\b=3, то очевидно, что для любых m кратных 3 выражение под синусом будет кратно Т.о. для заданного соотношения d и b не может наблюдаться каждый 3-й максимум.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 2119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.164.56 (0.012 с.) |

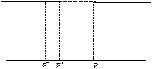

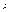 , лежащую против края щели, начало результирующего вектора переместится в середину спирали О.Конец вектора переместится по спирали в направлении полюса
, лежащую против края щели, начало результирующего вектора переместится в середину спирали О.Конец вектора переместится по спирали в направлении полюса  .При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг друга.Интенсивность света достигнет при этом минимума.При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти.Тоже самое будет происходить при смещении из точки P в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы (рис.1) и отличные от нуля минимумы (рис.3,4)
.При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг друга.Интенсивность света достигнет при этом минимума.При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти.Тоже самое будет происходить при смещении из точки P в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы (рис.1) и отличные от нуля минимумы (рис.3,4)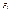 и
и 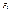 . Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных узких светлых и тёмных полос.
. Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных узких светлых и тёмных полос.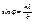 ,расстояние минимумов от центра картины возрастает с уменьшением
,расстояние минимумов от центра картины возрастает с уменьшением 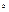 . Таким образом, с уменьшением ширины щели центральная светлая полоса расширяется, захватывая всё большую и большую область экрана.Если
. Таким образом, с уменьшением ширины щели центральная светлая полоса расширяется, захватывая всё большую и большую область экрана.Если 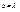 , то
, то 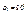 ,т.е. первый минимум соответствует углу
,т.е. первый минимум соответствует углу 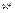 ; следовательно, он сдвинут на бесконечно удалённый край экрана. Освещённость экрана падает от центра к краям постепенно, асимптотически приближаясь к нулю; ширина центральной световой полосы возрастает беспредельно.Таким образом, с уменьшением b освещённость стремится стать равномерной по всему экрану.(рис5)
; следовательно, он сдвинут на бесконечно удалённый край экрана. Освещённость экрана падает от центра к краям постепенно, асимптотически приближаясь к нулю; ширина центральной световой полосы возрастает беспредельно.Таким образом, с уменьшением b освещённость стремится стать равномерной по всему экрану.(рис5)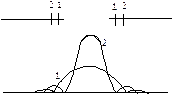
 ) мы получаем в центре резкое изображение линейного источника.
) мы получаем в центре резкое изображение линейного источника.
 (m=1,2,3,….)
(m=1,2,3,….)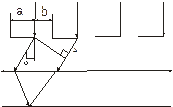
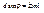 (m=1,2,3,…..) задаёт условие главных максимумов. Т.к.
(m=1,2,3,…..) задаёт условие главных максимумов. Т.к. 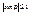 , то число главных максимумов будет определяться выражением
, то число главных максимумов будет определяться выражением 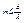


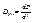
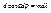
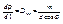
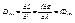 , где f – фокусное расстояние проецирующей линзы.
, где f – фокусное расстояние проецирующей линзы.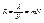

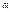 должно удовлетворять
должно удовлетворять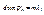 ,
, 
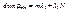
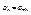
 или
или 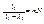
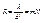
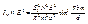
 и следовательно интенсивность будет равна 0.
и следовательно интенсивность будет равна 0.


