
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постулаты Бора. Теория атома водорода по Бору. Расчет энергетических состояний атома водорода с точки зрения теории Бора.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Первый постулат Бора: Атомы могут длительное время находиться только в определенных, так называемых стационарных состояниях, в которых атом не излучает и не поглощает энергию. Энергии стационарных состояний Второй постулат Бора: При переходе атома из одного начального стационарного состояния с энергией
Электроны в атомах совершают орбитальное движение вокруг ядра под действием кулоновских сил. Но орбитами могут быть только стационарные, определяемые условиями квантования. Действует 2-ой закон Ньютона: Совместное решение (2) и (3) дает: Зная
Спектральные линии возникают при переходе электронов с одного уровня на другой (более низкий), а энергия, испускаемая квантом, равна разности энергий этих двух уровней:
Cравнивая (1) и (7), можно вычислить постоянную Ридберга: Расчет энергетических состояний атома водорода: Физический смысл спектральных линий – монохроматические излучения, возникающие в результате перехода атома в данное состояние из всех возможных возбужденных состояний, расположенных выше. На рис. изображены уровни энергии атома водорода, а стрелками обозначены переходы между уровнями, соответствующие спектральным линиям. Из рисунка видно, что линии в спектре водорода можно разложить по сериям: для всех линий серии, значение остается постоянным, а m может принимать значения любые от m = n +1 до
В спектр испускания атома водорода входит несколько серий, расположенных в различных областях спектра: а) серия Лаймана - крайняя ультрафиолетовая область б) серия Бальмера - видимая и близкая ультрафиолетовая область
в) серия Пашена - инфракрасная область спектра г) серия Брэккета - инфракрасная область спектра д) серия Пфунда - инфракрасная область спектра Как видно из рисунка, головными линиями каждой серии являются линии, длины волн которых могут быть рассчитаны по формуле: Переходы, обозначенные жирными линиями, соответствуют головным линиям серии и определяются формулой (9): переходы на заштрихованные уровни соответствуют границе серии и определяются формулой (7), если в ней m = Метод квантования: орбиты электронов, соответствующие стационарным состояниям атомов, являются одними из возможных по классической механике орбит. Метод отбора орбит, соответствующих стационарным состояниям и называется методом квантования. Условие для круговых орбит:
44. Пользуясь соотношением неопределённости Гейзенберга, оценить минимальную энергию электрона в атоме водорода.
В соответствии с принципом неопределённости неопределённость координаты электрона связана с неопределённостью импульса следующим соотношением: Формально энергия была бы минимальной при r=0 и p=0. Поэтому положим (поскольку наши расчёты могут претендовать лишь на определение поряков вычисляемых величин, то мы половину в правой части опустили) Энергия в атоме водорода равна:
Найдём значение r, при котором Е минимальна. Продиффиренцировав последнее выражение по r и приравняв производную к нулю, получим уравнение
Подставим полученное нами значение для r в (*) получим выражение для минимальной энергии:
Квантовомеханическая теория атома водорода. Собственное значения и собственные функции для стационарных состояний атома водорода. Орбитальный момент электрона по квантовой теории. Гиромагнитное отношение. Атом водорода – простейшая система для которой были получены точные решения уравнений квантовой механики. Уравнение Шредингера Поскольку потенциальная энергия сферически симметрична, то оператор Лапласа в уравнении Шредингера лучше взять в сферических координатах. По этой причине Уравнение Шредингера в следствии сферической симметрии разлаживается на 3 уравнения, каждое из которых зависит только от одной переменной. На она должна быть однозначной должна быть непрерывной должна быть конечной. Так как Так как энергия сферически симметрична, а также из условия однозначности волновой функции следует, что функции Функция Функции должны быть непрерывными, однозначными и конечными исходя из физического смысла – а именно вероятность не может быть >1 или бесконечной. Угловая функция зависит от l m, и при решении уравнения Шредингера она определяет момент импульса Решение радиального уравнения приводит к специальной функции – полином Лагерра и квадрат этой функции определяет вероятность обнаружения электрона на определенном расстоянии от ядра.
Имеется соответствие атом водорода в квантовой механике решается абсолютно точно квантовые числа n, l и m получаются как следствия решения этого уравнения. В то же время результаты квантовой механики и результаты Бора совпадают, а именно: уравнение Шредингера дает максимум вероятности на боровских орбитах. Гиромагнитное отношение – отношение модуля магнитного момента в единицах
|
|||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 …образуют дискретный спектр.
…образуют дискретный спектр.  (2) Момент импульса электрона в этих состояниях должен быть целым кратным от постоянной Планка.
(2) Момент импульса электрона в этих состояниях должен быть целым кратным от постоянной Планка. в другое конечное состояние с энергией
в другое конечное состояние с энергией  происходит излучение кванта света, причем
происходит излучение кванта света, причем  .
.  (3),
(3), (4).
(4).
 и
и  можно найти:
можно найти:  ,
, , можно найти полную энергию электрона в атоме водорода:
, можно найти полную энергию электрона в атоме водорода: (5).
(5). (6),
(6), , здесь h - постоянная Планка, равная 6,625 *10-34 Дж.с. Из (6) и (13) следует, что длины волн спектральных линий атома водорода описываются формулой, аналогичной (1):
, здесь h - постоянная Планка, равная 6,625 *10-34 Дж.с. Из (6) и (13) следует, что длины волн спектральных линий атома водорода описываются формулой, аналогичной (1):  (7).
(7). (8), где e - заряд электрона, m - его масса,
(8), где e - заряд электрона, m - его масса,  - электрическая постоянная, равная 8,85*10-12 Ф/м.
- электрическая постоянная, равная 8,85*10-12 Ф/м.
 эВ
эВ .
.
 ,где n =1, m =2,3,.....
,где n =1, m =2,3,.....  , где n =2, m =3,4,5,....
, где n =2, m =3,4,5,....  , где n =3, m =4,5,6....
, где n =3, m =4,5,6....  , где n =4, m =5,6,7,....
, где n =4, m =5,6,7,....  , где n =5, m =6,7,...
, где n =5, m =6,7,... 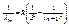 (9)
(9) (10) Особый интерес представляет граница серии Лаймана. Зная частоту граничной серии Лаймана, можно определить энергию, необходимую для отрыва электрона от атома водорода, находящегося в нормальном или основном состоянии с n =1. Эта энергия называется энергией ионизации и вычисляется по формуле:
(10) Особый интерес представляет граница серии Лаймана. Зная частоту граничной серии Лаймана, можно определить энергию, необходимую для отрыва электрона от атома водорода, находящегося в нормальном или основном состоянии с n =1. Эта энергия называется энергией ионизации и вычисляется по формуле: 
 - магнитное квантовое число, которое при заданном может принимать значения
- магнитное квантовое число, которое при заданном может принимать значения  , т.е. всего 2 значений. Оно определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+ 1 ориентаций.
, т.е. всего 2 значений. Оно определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+ 1 ориентаций.
 и
и  Подставив эти значения в 1 получим соотношение:
Подставив эти значения в 1 получим соотношение: 


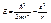 (*)
(*)


 , где
, где  ,
,  - волновая функция. В сферических координатах
- волновая функция. В сферических координатах  . Решить уравнение Шредингера это значит найти собственные значения энергии
. Решить уравнение Шредингера это значит найти собственные значения энергии  и собственные функции
и собственные функции  . Все уравнения отличаются только значением
. Все уравнения отличаются только значением  .
.  - для атома водорода и водородоподобных систем.
- для атома водорода и водородоподобных систем. , где
, где  .
. , где
, где  - радиальная функция,
- радиальная функция,  - угловая функция,
- угловая функция,  .
. - квадрат определяет вероятность найти данную частицу в единице объема с коэффициентами x, y, z. Т. е. Квадрат этой функции – плотность вероятности. Исходя из физического смысла
- квадрат определяет вероятность найти данную частицу в единице объема с коэффициентами x, y, z. Т. е. Квадрат этой функции – плотность вероятности. Исходя из физического смысла  , т. к. это достоверное событие и это уравнение называется уравнением нормировки.
, т. к. это достоверное событие и это уравнение называется уравнением нормировки. являются функциями целочисленного аргумента m который может принимать значения
являются функциями целочисленного аргумента m который может принимать значения  и так далее.
и так далее. непрерывная и однозначная является спец. Функцией – присоединенные функции Лежандра. Они имеют однозначные и конечные решения только при целочисленных значениях l, которые иногда могут быть отрицательными и связано с m: m=-l,…,0,…l.
непрерывная и однозначная является спец. Функцией – присоединенные функции Лежандра. Они имеют однозначные и конечные решения только при целочисленных значениях l, которые иногда могут быть отрицательными и связано с m: m=-l,…,0,…l. и проекцию момента импульса на выделенное направление
и проекцию момента импульса на выделенное направление  , а с точки зрения графического решения она определяет форму электронного облака и его ориентацию.
, а с точки зрения графического решения она определяет форму электронного облака и его ориентацию. , где z – порядковый номер элемента,
, где z – порядковый номер элемента,  - полином Лагерра,
- полином Лагерра,  - боровский первый радиус
- боровский первый радиус  .
. , иначе
, иначе  , где
, где  - безразмерное число гиромагнитное отношение – характеризует соотношение между магнитным и механическим моментами системы.
- безразмерное число гиромагнитное отношение – характеризует соотношение между магнитным и механическим моментами системы.


