
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращательное движение твердого тела вокруг неподвижной осиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим приложения общих теорем динамики к задачам о движении абсолютно твердого тела. Так как изучение поступательного движения твердого тела сводится к задачам динамики точки, то начнем с рассмотрения вращательного движения вокруг неподвижной оси. Пусть на твердое тело, имеющее неподвижную ось вращения
Рис. 321 Будем в дальнейшем величину Подставляя в предыдущее равенство значение
Уравнение (66) представляет собой дифференциальное уравнение вращательного движения твердого тела. Из него следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающемуся моменту:
Равенство (66) показывает, что при данном Следовательно, момент инерции тела действительно играет при вращательном движении такую же роль, как масса при поступательном, т. е. является мерой инертности тела при вращательном движении (см. § 102). Уравнение (66) позволяет: 1) зная закон вращения тела, т. е. Вместо уравнения (66) для изучения вращательного движения можно также пользоваться теоремой об изменении кинетической энергии: Отметим следующие частные случаи: 1) если 2) если Уравнение (66) по своему виду аналогично дифференциальному уравнению прямолинейного движения точки (см. § 77). Поэтому имеется аналогия и между самими названными движениями, и все результаты, получаемые для прямолинейного движения точки, будут справедливы и для вращательного движения твердого тела, если в них заменить соответственно силу F, массу При решении задач уравнением (66) целесообразно пользоваться тогда, когда система состоит только из одного вращающегося тела. Если в системе кроме .Моме́нтине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения в Международной системе единиц (СИ): кг·м². Обозначение: I или J.Теоре́маГю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции
где
Теорема названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса 9.Динамика вращательного движения АТТ вокруг неподвижной оси. Основной закон. Момент силы. Работа внешних сил. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ Основные формулы • Момент силы F,действующей на тело, относительно оси вращения
где • Момент инерции относительно оси вращения: а) материальной точки J=mr2, где т —масса точки;r —расстояние ее от оси вращения; б) дискретного твердого тела
где в) сплошного твердого тела
Если тело однородно, т. е. его плотность dm=dV и где V —объем тела. • Моменты инерции некоторых
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторнаяфизическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Работа внешних сил при вращении твердого тела вокруг неподвижной оси
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1013; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.012 с.) |

 (рис. 321), действует система заданных сил
(рис. 321), действует система заданных сил  Одновременно на тело действуют реакции подшипников RA и
Одновременно на тело действуют реакции подшипников RA и  Чтобы исключить из уравнения движения эти наперед не известные силы, воспользуемся теоремой моментов относительно оси z (см. § 116). Так как моменты сил RA и RB относительно оси z равны нулю, то получим
Чтобы исключить из уравнения движения эти наперед не известные силы, воспользуемся теоремой моментов относительно оси z (см. § 116). Так как моменты сил RA и RB относительно оси z равны нулю, то получим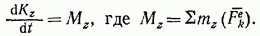

 называть вращающим моментом.
называть вращающим моментом. найдем
найдем

 чем больше момент инерции тела, тем меньше угловое ускорение, и наоборот.
чем больше момент инерции тела, тем меньше угловое ускорение, и наоборот. найти вращающий момент
найти вращающий момент  зная вращающий момент
зная вращающий момент  найти
найти  , т. е. закон вращения тела, или найти его угловую скорость
, т. е. закон вращения тела, или найти его угловую скорость  . При решении второй задачи следует иметь в виду, что в общем случае величина
. При решении второй задачи следует иметь в виду, что в общем случае величина  может быть переменной и зависеть от
может быть переменной и зависеть от 
 где Т и
где Т и  определяются по формулам (43) и (47).
определяются по формулам (43) и (47). то
то  , т. е. тело вращается равномерно;
, т. е. тело вращается равномерно; то
то  , т. е. тело вращается равнопеременно.
, т. е. тело вращается равнопеременно. , координату
, координату  скорость v и ускорение а точки на вращающий момент
скорость v и ускорение а точки на вращающий момент  момент инерции
момент инерции  угол поворота
угол поворота  угловую скорость
угловую скорость  и угловое ускорение в вращающегося тела.
и угловое ускорение в вращающегося тела.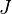 тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела
тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела 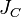 относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния
на квадрат расстояния  между осями[1]:
между осями[1]: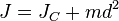
 ,
,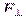 — проекция силы F на плоскость, перпендикулярную оси вращения; l — плечо силы F (кратчайшее расстояние от оси вращения до линии действия силы).
— проекция силы F на плоскость, перпендикулярную оси вращения; l — плечо силы F (кратчайшее расстояние от оси вращения до линии действия силы).
 — масса i-го элемента тела; ri — расстояние этого элемента от оси вращения; п — число элементов тела;
— масса i-го элемента тела; ri — расстояние этого элемента от оси вращения; п — число элементов тела;
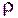 одинакова по всему объему, то
одинакова по всему объему, то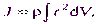


 Рис. 2.12
Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr. При том же самом угле поворота dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная
Рис. 2.12
Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr. При том же самом угле поворота dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная  , ни вторая производная
, ни вторая производная  не могут служить характеристикой движения всего твердого тела. За это же время dt радиус-вектор
не могут служить характеристикой движения всего твердого тела. За это же время dt радиус-вектор  , проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться). Угол поворота dφ характеризует перемещение всего тела за время dt. Удобно ввести
, проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться). Угол поворота dφ характеризует перемещение всего тела за время dt. Удобно ввести  – вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора
– вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора 

 ,
,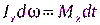 . Подставив это выражение в последнее уравнение для δA и учитывая, что
. Подставив это выражение в последнее уравнение для δA и учитывая, что  , получим
, получим . (5.19)
. (5.19) . (5.20)
. (5.20)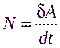 , вызывающих вращение вокруг неподвижной оси. Учитывая, что
, вызывающих вращение вокруг неподвижной оси. Учитывая, что  , получим:
, получим: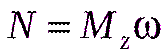 Таким образом, мощность внешних сил, вызывающих вращение твердого тела вокруг неподвижной оси определяется моментом Mz этих сил относительно данной оси и угловой скоростью вращения.
Таким образом, мощность внешних сил, вызывающих вращение твердого тела вокруг неподвижной оси определяется моментом Mz этих сил относительно данной оси и угловой скоростью вращения.


