
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Киниматика абсолютно твердого тела. Поступательное движение твердого тела.Содержание книги
Поиск на нашем сайте
Киниматика материальной точки. Системы отсчета. Два способа описания движения материальной точки. Скорость и ускорение произвольно движущейся м.т. как производные радиуса вектора (первый способ описания движения). Материальная точка – модель реального тела размерами, которого в данных условиях можно пренебречь. При этом масса тела считается сосредоточенной в геометрической точке. Система отсчета – система координат, жестко связанная с абсолютно твердым телом, снабженная часами и используемая для определения положения в пространстве тел или их частей в любые моменты времени. Иногда система отсчета называют хронометрированной системой координат. Тело отсчета – абсолютно твердое тело, с которым жестко связана система координат. Обычно это инерциальная система отсчета. Описать движение материальной точки, значит указать положение этой точки в любой момент времени. I Векторный способ.
Положение м.т. задается радиус вектором проведенным из некоторой неподвижной точки О в выбранной С.О. в т.М
Если найти эту зависимость то можно сказать что описали движение материальной точки. II Координатный способ С выбранным телом отсчета жестко связывают определенную систему координат. Запишим проекции на оси декартовой системы координат радиус-вектора r(t). Зная зависимость этих координат от времени (закон движения м.т.) можно найти положение точки в каждый момент времени, а так же ее скорость и ускорение.
Скорость – векторная величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Первая производная перемещения по времени. Вектором средней скорости называется отношение приращения радиус-вектора точки к промежутку времени. <υ>=Δr/Δt.
Мгновенная скорость – векторная величина, определяемая производной радиус-вектора движущейся точки по времени. υ=dr/dt. Ускорение – это характеристика неравномерного движения; определяет быстроту изменения скорости по модулю и направлению. Вторая производная перемещения по времени. Среднее ускорение неравномерного движения за промежуток времени – это векторная величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло. <a>=Δυ/Δt. Мгновенным ускорением материальной точки в момент времени t будет предел среднего ускорения. a=dυ/dt. Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории.) aτ=dυ/dt. Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории). an=υ2/r. Киниматика абсолютно твердого тела. Поступательное движение твердого тела. Энергия кинетическая и потенциальная. Полная механическая энергия и закон ее сохранения. Примеры применения законов сохранения энергии. Кинетическая энергия – та часть механической энергии, которая зависит от скорости движения частей системы. Потенциальная энергия – это та часть механической энергии, которая зависит от временного расположения тел системы и характера взаимодействия между ними. Отдельная материальная точка обладает тока кинетической энергией, потенциальная энергия может быть принадлежностью только системы тел. Полная механическая энергия системы – это энергия механического движения и взаимодействия, т.е. сумма кинетической и потенциальной энергии. Фундаментальным законом природы является общефизический закон сохранения энергии: В изолированной системе энергия может переходить из одной формы в другую, но ее количество остается постоянным. Энергия характеризует состояние системы, а закон ее сохранения относится к числу строгих законов. Закон сохранения механической энергии является обобщением опытных фактов, он связан с однородностью времени. Энергию покоящейся как целую механическую систему обычно называют внутренней. Она обычно включает в себя кинетическую энергию движущихся частиц системы и потенциальную их взаимодействия. Энергия механической системы зависит от скорости движения и взаимного расположения частей системы. Е = Ек + Ер Киниматика материальной точки. Системы отсчета. Два способа описания движения материальной точки. Скорость и ускорение произвольно движущейся м.т. как производные радиуса вектора (первый способ описания движения). Материальная точка – модель реального тела размерами, которого в данных условиях можно пренебречь. При этом масса тела считается сосредоточенной в геометрической точке. Система отсчета – система координат, жестко связанная с абсолютно твердым телом, снабженная часами и используемая для определения положения в пространстве тел или их частей в любые моменты времени. Иногда система отсчета называют хронометрированной системой координат. Тело отсчета – абсолютно твердое тело, с которым жестко связана система координат. Обычно это инерциальная система отсчета. Описать движение материальной точки, значит указать положение этой точки в любой момент времени. I Векторный способ.
Положение м.т. задается радиус вектором проведенным из некоторой неподвижной точки О в выбранной С.О. в т.М
Если найти эту зависимость то можно сказать что описали движение материальной точки. II Координатный способ С выбранным телом отсчета жестко связывают определенную систему координат. Запишим проекции на оси декартовой системы координат радиус-вектора r(t). Зная зависимость этих координат от времени (закон движения м.т.) можно найти положение точки в каждый момент времени, а так же ее скорость и ускорение.
Скорость – векторная величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Первая производная перемещения по времени. Вектором средней скорости называется отношение приращения радиус-вектора точки к промежутку времени. <υ>=Δr/Δt.
Мгновенная скорость – векторная величина, определяемая производной радиус-вектора движущейся точки по времени. υ=dr/dt. Ускорение – это характеристика неравномерного движения; определяет быстроту изменения скорости по модулю и направлению. Вторая производная перемещения по времени. Среднее ускорение неравномерного движения за промежуток времени – это векторная величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло. <a>=Δυ/Δt. Мгновенным ускорением материальной точки в момент времени t будет предел среднего ускорения. a=dυ/dt. Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории.) aτ=dυ/dt. Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории). an=υ2/r. Киниматика абсолютно твердого тела. Поступательное движение твердого тела.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |


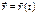 - основной закон описания движения материальной точки.
- основной закон описания движения материальной точки.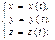 Мгновенная скорость – это векторная величина, определяемая производной радиус-вектора движущейся точки по времени. υ=limΔt→0Δr/Δt.
Мгновенная скорость – это векторная величина, определяемая производной радиус-вектора движущейся точки по времени. υ=limΔt→0Δr/Δt.


