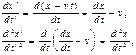Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод основного уравнения динамики вращательного движения абсолютно твердого тела. Момент импульса материальной точки и твердого тела. Закон сохранения момента импульса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формулировка закона: Скорость изменения момента импульса относительно полюса равна главному моменту силы относительно того же полюса, т.е. В проекциях на оси координат: Если вращение тела происходит относительно неподвижной оси, то основной закон динамики вращательного движения примет вид:
Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: Момент импульса – псевдовекторная величина. Направление этого вектора находится по тому же правилу, сто и нахождение момента силы (вращение рукоятки буравчика по направлению вектора скорости) Моментом импульса системы материальных точек относительно полюса называется векторная величина, равная векторной сумме моментов импульсов относительно полюса всех материальных точек системы, т.е. Моментом импульса материальной точки относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса этой точки относительно произвольной точки данной оси. Моментом импульса системы материальных точек относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса системы относительно произвольной точки данной оси. В частном случае вращательного движения точки по окружности, момент её импульса равен:
Физический смысл момента импульса: Момент импульса характеризует интенсивность вращательного движения. закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени. Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчёта (относительно поворота замкнутой системы в пространстве на любой угол).
17. Элементы специальной теории относительности. Принцип относительности в классической механике. Преобразования Галилея. Постулаты специальной теории относительности. Преобразования Лоренца. Альберт Эйнштейн заложил основы специальной теории относительности. Постулаты Эйнштейна, сформулированные им в 1905г. 1. Принцип относительности: никакие опыты (механические, электрические, оптические), проведённые внутнри данной инерциальной системы отсчёта не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчёта к другой. 2. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчёта. Анализ явлений в инерциальных системах отсчета, проведенный А.Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними и, следовательно, должны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности. Рассмотрим две инерциальные системы отсчета: K (с координатами x, y, z) и К’ (с координатами x’, y’, z’), движущуюся относительно К (вдоль оси x) со скоростью υ=const. Преобразования Лоренца имеют вид K→K’ x’=(x-υt)/(1-β2), y’=y, z’=z, t’=[t-(υx)/c2]/(1-β2). K’→K x=(x’+υt’)/(1-β2), y=y’, z=z’, t=[t’+(υx’)/c2]/(1-β2). β=υ/c. Галилей еще в XVII в. сформулировал принцип относительности в механике, или механический принцип относительности. Механический принцип относительности. Механические явления во всех инерциальных системах отсчета происходят совершенно одинаково. Нельзя с помощью механических экспериментов, производимых в движущейся инерциальной системе отсчета, определить скорость ее движения (если не производить наблюдений тел из системы отсчета, относительно которой мы хотим определить скорость движения).
Покажем, что уравнения механики математически записываются совершенно одинаково во всех инерциальных системах отсчета. Для простоты рассмотрим движение материальной точки, т.е. тела, размерами которого можно пренебречь в рассматриваемой ситуации. Пусть это движение описывается в двух каких-нибудь инерциальных системах - в “покоящейся” системе K и в “движущейся” системе K'. Пусть в начальный момент времени декартовы оси этих систем совпадали и пусть система K движется вдоль оси x с постоянной скоростью v. Координаты точки M, отсчитываемые относительно движущейся и относительно покоящейся систем отсчета K и K' связаны следующими формулами преобразования:
которые называют формулами преобразования Галилея. Время при преобразованиях Галилея никак не преобразуем, так что следует положить, что
Эту формулу тоже будем относить к формулам преобразования Галилея. Рассмотрим движение материальной точки M массы m относительно той и другой систем, происходящее, к примеру, вдоль оси x, под действием некоторой заданной силы F (действующей только вдоль оси x). Тогда в системах K и K' имеем следующие уравнения движения:
которые математически совершенно одинаковы (инвариантны). При этом одно уравнение получается из другого с помощью преобразований Галилея. Действительно, согласно этим преобразованиям:
вполне определённой внутренней энергией (она не зависит от того, как система пришла в данное состояние). Анализ явлений в инерциальных системах отсчета, проведенный А.Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними и, следовательно, должны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.01 с.) |


 .
. . В данном случае момент импульса легко выразить через угловую скорость и момент инерции тела относительно рассматриваемой оси:
. В данном случае момент импульса легко выразить через угловую скорость и момент инерции тела относительно рассматриваемой оси:  . Тогда основной закон динамики вращательного движения примет вид:
. Тогда основной закон динамики вращательного движения примет вид:  . Если тело не рассыпается и не деформируется, то
. Если тело не рассыпается и не деформируется, то , вследствие чего
, вследствие чего  . Если ко всему
. Если ко всему  , то
, то  и, оно равно:
и, оно равно:  .
. (*). Полная работа
(*). Полная работа 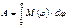 Если
Если  , то
, то  На основании формулы (*), получим выражение для кинетической энергии вращательного движения твёрдого тела относительно неподвижной оси. Т.к.
На основании формулы (*), получим выражение для кинетической энергии вращательного движения твёрдого тела относительно неподвижной оси. Т.к.  , то
, то  . После интегрирования, получим окончательный результат для кинетической энергии вращательного движения относительно неподвижной оси
. После интегрирования, получим окончательный результат для кинетической энергии вращательного движения относительно неподвижной оси  .
. , где
, где  - масса, радиус-вектор и скорость «i- ой» точки системы.
- масса, радиус-вектор и скорость «i- ой» точки системы. , где a - угол между радиусом окружности и скоростью.
, где a - угол между радиусом окружности и скоростью.

 .
.