
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении момента количества движения системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теорема. Производная по времени от момента количества движения системы, взятого относительно какого-нибудь центра, равна векторной сумме моментов внешних сил, действующих на систему относительно того же центра.
Доказательство: Теорема об изменении момента количества движения для
Сложим все
что и требовалось доказать. Теорема. Производная по времени от момента количества движения системы, взятого относительно какой-либо оси, равна векторной сумме моментов внешних сил, действующих на систему относительно той же оси. Для доказательства достаточно спроектировать векторное уравнение (6.3) на эту ось. Для оси
Теорема об изменении момента количества движения системы относительно центра масс. (без доказательства) Для осей движущихся поступательно вместе с центром масс системы, теорема об изменении момента количества движения системы относительно центра масс сохраняет тот же вид, что и относительно неподвижного центра.
Законы сохранения момента количества движения. 1. Если главный момент внешних сил системы относительно точки 2. Если сумма моментов всех внешних сил системы относительно какой-либо оси равна нулю (
Кинетическая энергия системы. Кинетической энергией системы называют сумму кинетических энергий всех точек системы.
Теорема Кенига. Кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы при ее движении относительно центра масс.
Доказательство: Рассмотрим движение механической системы относительно двух систем координат. Одна система неподвижна, другая, с началом в центре масс системы, перемещается относительно первой поступательно.
Так как
Кинетическая энергия твердого тела. 1. Поступательное движение тела. Кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для одной точки, у которой масса равна массе этого тела.
2. Вращение тела вокруг неподвижной оси. Кинетическая энергия твердого тела при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
3. Плоское движение тела. Кинетическая энергия твердого тела при плоском движении складывается из кинетической энергии тела вместе с центром масс и кинетической энергии тела от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения..
Теорема об изменении кинетической энергии системы. Эта теорема существует в двух формах. Теорема. Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.
Доказательство: Теорема об изменении кинетической энергии для
Сложим все
или или что и требовалось доказать. Теорема. Изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек системы при том же перемещении системы..
|
||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (6.3)
(6.3) точки имеет вид:
точки имеет вид: ,
, 
 уравнений и получим:
уравнений и получим: или
или  это будет выглядеть так:.
это будет выглядеть так:. (6.4)
(6.4) равен нулю (
равен нулю ( ), то момент количества движения системы относительно точки
), то момент количества движения системы относительно точки 
 ), то момент количества движения системы относительно этой оси является постоянной величиной.
), то момент количества движения системы относительно этой оси является постоянной величиной. 


 ,
,  - радиус-вектор и абсолютная скорость
- радиус-вектор и абсолютная скорость  точки соответственно;
точки соответственно; ,
,  - радиус-вектор и абсолютная скорость центра масс системы соответственно;
- радиус-вектор и абсолютная скорость центра масс системы соответственно; ,
,  - радиус-вектор
- радиус-вектор  ,
,  (так как переносное движение поступательное)
(так как переносное движение поступательное)

 , то
, то или
или  ,
,  - скорость любой точки твердого тела
- скорость любой точки твердого тела ,
, 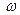 - угловая скорость вращения твердого тела.
- угловая скорость вращения твердого тела. ,
,  - скорость центра масс твердого тела,
- скорость центра масс твердого тела, 
 ,
, 






