
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении количества движения механической системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Количество движения системы, как векторная величина, определяется формулами (4.12) и (4.13). Теорема. Производная от количества движения системы по времени равна геометрической сумме всех действующих на нее внешних сил.
В проекциях декартовые оси получим скалярные уравнения.
Можно записать векторное
и скалярные уравнения
Которые выражают теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов за тот же промежуток времени. При решении задач чаще используются уравнения (4.27) Закон сохранения количества движения
Теорема об изменении кинетического момента Теорема об изменении момента количества движения точки относительно центра: производная по времени от момента количества движения точки относительно неподвижного центра равна векторному моменту, действующей на точку силы относительно того же центра.
Сравнивая (4.23) и (4.30), видим, что моменты векторов
Это равенство выражает теорему момента количества движения точки относительно оси.
Если спроектировать выражение (4.32) на ось
Подставляя (4.10) в равенство (4.33) можно записать дифференциальное уравнение вращающегося твердого тела (колес, осей, валов, роторов и т.д.) в трех формах.
Таким образом, теорему об изменении кинетического момента целесообразно использовать для исследования весьма распространенного в технике движения твердого тела, его вращения вокруг неподвижной оси.
Закон сохранения кинетического момента системы 1. Пусть в выражении (4.32) Тогда из уравнения (4.32) следует, что 2. Если Эти результаты выражают собой закон сохранения кинетического момента. В случае вращающегося твердого тела из равенства (4.34) следует, что, если Если система неизменяема (абсолютно твердое тело), то Если система изменяема, то Вторая задача Д2 контрольной работы посвящена теореме об изменении кинетического момента системы относительно оси.
Задача Д2 Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами R и 2R, где R = 1,2м) массой В момент времени Определить, пренебрегая массой вала, зависимость На всех рисунках груз D показан в положении, при котором s > 0 (когда s < 0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии OC = b от центра C. Указания. Задача Д2 – на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент При решении задачи полезно изобразить на вспомогательном чертеже вид на платформу сверху (с конца z), как это сделано на рис. Д2,0,а – Д2,9, а. Момент инерции пластины с массой m относительно оси Cz, перпендикулярной пластине и проходящей через ее центр масс, равен: для прямоугольной пластины со сторонами
Для круглой пластины радиуса R
Пример Д2. Однородная горизонтальная платформа (прямоугольная со сторонами 2l и l), имеющая массу Дано: m1 = 16 кг, т2 = 10 кг, l = 0,5 м, Решение. Рассмотрим механическую систему, состоящую из платформы и груза D. Для определения w применим теорему об изменении кинетического момента системы относительно оси z:
Изобразим действующие на систему внешние силы: силы тяжести
Умножая обе части этого уравнения на dt и интегрируя, получим
Для рассматриваемой механической системы
где Так как платформа вращается вокруг оси z, то Но, как известно,
Тогда
Следовательно,
Для определения
Но на рис. Д2 б видно, что OD2
Тогда уравнение (3), где k = 6, примет вид
Постоянную интегрирования определяем по начальным условиям: при
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 942; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.69.109 (0.008 с.) |

 (4.26)
(4.26) (4.27)
(4.27) (4.28)
(4.28) (4.29)
(4.29) , то
, то  . Следовательно, если сумма внешних сил равна нулю, то вектор количества движения будет постоянен (постоянны и модуль и направление).
. Следовательно, если сумма внешних сил равна нулю, то вектор количества движения будет постоянен (постоянны и модуль и направление). следует
следует  . При этом порядок системы дифференциальных уравнений снижается на единицу. Отметим, что теоремы о движении центра масс системы и об изменении количества движения удобно использовать при исследовании поступательных движениях механических систем, в частности твердых тел.
. При этом порядок системы дифференциальных уравнений снижается на единицу. Отметим, что теоремы о движении центра масс системы и об изменении количества движения удобно использовать при исследовании поступательных движениях механических систем, в частности твердых тел. или
или  (4.30)
(4.30) и
и  связаны такой же зависимостью, какой связаны сами векторы
связаны такой же зависимостью, какой связаны сами векторы  , проходящую через центр О, то получим
, проходящую через центр О, то получим
 (4.31)
(4.31) (4.32)
(4.32) , проходящей через центр О, то получим равенство, характеризующее теорему об изменении кинетического момента относительно оси.
, проходящей через центр О, то получим равенство, характеризующее теорему об изменении кинетического момента относительно оси.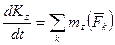 (4.33)
(4.33) (4.34)
(4.34) (4.35)
(4.35) (4.36)
(4.36)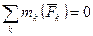 .
. , т.е. если сумма моментов всех приложенных к системе вешних сил относительно данного центра равно нулю, то кинетический момент системы относительно этого центра будет численно и по направлению будет постоянен.
, т.е. если сумма моментов всех приложенных к системе вешних сил относительно данного центра равно нулю, то кинетический момент системы относительно этого центра будет численно и по направлению будет постоянен. , то
, то  . Таким образом, если сумма моментов действующих на систему внешних сил относительно некоторой оси равна нулю, то кинетический момент системы относительно этой оси будет величиной постоянной.
. Таким образом, если сумма моментов действующих на систему внешних сил относительно некоторой оси равна нулю, то кинетический момент системы относительно этой оси будет величиной постоянной. . Отсюда приходим к следующим выводам:
. Отсюда приходим к следующим выводам: , следовательно, и
, следовательно, и  и твердое тело вращается вокруг неподвижной оси с постоянной угловой скоростью.
и твердое тело вращается вокруг неподвижной оси с постоянной угловой скоростью. . При увеличении
. При увеличении  (тогда отдельные элементы системы удаляются от оси вращения) угловая скорость
(тогда отдельные элементы системы удаляются от оси вращения) угловая скорость 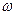 уменьшается, т.к.
уменьшается, т.к.  , а при уменьшении
, а при уменьшении  увеличивается, таким образом, в случае изменяемой системы с помощью внутренних сил можно изменить угловую скорость.
увеличивается, таким образом, в случае изменяемой системы с помощью внутренних сил можно изменить угловую скорость. кг вращается с угловой скоростью
кг вращается с угловой скоростью  вокруг вертикальной оси z, отстоящей от центра масс C платформы на расстоянии OC = b (рис. Д2,0 – Д2,9, табл. Д2); размеры для всех прямоугольных платформ показаны на рис. Д2,0а (вид сверху).
вокруг вертикальной оси z, отстоящей от центра масс C платформы на расстоянии OC = b (рис. Д2,0 – Д2,9, табл. Д2); размеры для всех прямоугольных платформ показаны на рис. Д2,0а (вид сверху). по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой
по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой  кг по закону
кг по закону  , где s выражено в метрах, t - в секундах. Одновременно на платформы начинает действовать пара сил с моментом M (задан в ньютонометрах; при M < 0 его направление противоположно показанному на рисунках).
, где s выражено в метрах, t - в секундах. Одновременно на платформы начинает действовать пара сил с моментом M (задан в ньютонометрах; при M < 0 его направление противоположно показанному на рисунках). т.е. угловую скорость платформы, как функцию времени.
т.е. угловую скорость платформы, как функцию времени. системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость груза складывается из относительной
системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость груза складывается из относительной  и переносной
и переносной  скоростей, т.е.
скоростей, т.е.  . Поэтому и количество движения этого груза
. Поэтому и количество движения этого груза  . Тогда можно воспользоваться теоремой Вариньона (статика), согласно которой
. Тогда можно воспользоваться теоремой Вариньона (статика), согласно которой  ; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д2.
; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д2. и
и
 ;
;
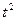 0.6
0.6  -0.5t
-0.6t
0.8t
0.4
-0.5t
-0.6t
0.8t
0.4 









 жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угловой скоростью
жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угловой скоростью  (рис. Д2а ). В момент времени
(рис. Д2а ). В момент времени  , находящийся в желобе АВ в точке С, начинает двигаться по желобу (под действием внутренних сил) по закону s = CD = F(t).
, находящийся в желобе АВ в точке С, начинает двигаться по желобу (под действием внутренних сил) по закону s = CD = F(t). , s = 0,4t2 (s — в метрах, t — в секундах), М = kt, где k =6 Нм/с. Определить:
, s = 0,4t2 (s — в метрах, t — в секундах), М = kt, где k =6 Нм/с. Определить:  (1)
(1) реакции
реакции  и вращающий момент M. Так как силы
и вращающий момент M. Так как силы  и
и  параллельны оси z, а реакции
параллельны оси z, а реакции  и
и  эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление
эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление  и уравнение (1) примет такой вид:
и уравнение (1) примет такой вид: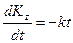 (2)
(2) (3)
(3) (4)
(4) и
и  — кинетические моменты платформы и груза D соответственно.
— кинетические моменты платформы и груза D соответственно. . Значение Izнайдем по теореме Гюйгенса:
. Значение Izнайдем по теореме Гюйгенса:  (
( — момент инерции относительно оси
— момент инерции относительно оси  , параллельной оси z и проходящей через центр С платформы).
, параллельной оси z и проходящей через центр С платформы).

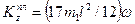 (5)
(5) . Так как груз D движется по закону s = CD = 0,4t2, то
. Так как груз D движется по закону s = CD = 0,4t2, то  ; изображаем вектор
; изображаем вектор  численно
численно  . Тогда, по теореме Вариньона,
. Тогда, по теореме Вариньона, (6)
(6) . Подставляя эту величину в равенство (6), а затем значения
. Подставляя эту величину в равенство (6), а затем значения  (7)
(7) (8)
(8)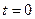 ,
, 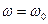 . Получим
. Получим  =
= 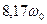 = 16,34. При этом значении
= 16,34. При этом значении  , где t — в секундах,
, где t — в секундах, 


