
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении количества движения механической системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Количеством движения механической системы называется вектор, равный геометрической сумме (главному вектору) количеств движения всех материальных точек этой системы.
Вектор количества движения механической системы имеет модуль, равный произведению массы системы на скорость ее центра масс и направление этой скорости. Проецируем вектор
Проекция количества движения механической системы на каждую координатную ось, равная сумме проекций количеств движения всех точек системы на одну ос, определяется произведением массы системы на проекцию скорости центра масс на эту же ось. Дифференцируем (1) по времени:
Согласно уравнению движения центра масс системы,
Следовательно, Уравнение (3) выражает теорему об изменении количества движения механической системы в дифференциальной форме: производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. Векторному уравнению (3) соответствуют три уравнения в проекциях оси координат:
Уравнения (4) показывают, что производная по времени от проекции количества движения механической системы на любую ось равна проекции главного вектора внешних сил, действующих на систему, на ту же ось. Из уравнений (3) и (4) следует, что изменение количества движения механической системы вызывается только внешними силами.
С л е д с т в и я и з т е о р е м ы; 1. Если главный вектор внешних сил за рассматриваемой промежуток времени равен нулю, то количество движения механической системы постоянно. Из уравнения (3) следует, что если т.е. 2. Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна. Так, например, при
Следствия из теорем об изменении количества движения механической системы выражают закон сохранения количества движения системы. ЗАДАЧА Д2 Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1 =18 кг, движущейся вдоль горизонтальных направляющих, и груза D массой m2 =6 кг (рис. Д2.0-Д2.9, табл. Д2). В момент времени t0 =0, когда скорость плиты U0 =2 м/с, груз под действием внутренних сил начинает двигаться по желобу плиты. На рис 0-3 желоб КЕ прямолинейный и при движении груза расстояние S =АД изменяется по закону Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить зависимость Указания. Задача Д2 на применение теоремы об изменении количества движения системы. При решении составить уравнение, выражающее теорему, в проекции на горизонтальную ось.
Таблица Д 2
3.2.2. Пример решения задачи Д2. В центре тяжести А тележки массой m1, движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень А D длиной t0 =0, когда скорость тележки U=U0 стержень А D начинает вращаться вокруг оси А по закону Д а н о: m1 =24 кг, m2 =12 кг, U0 =0,5 м/с, Решение. Рассмотрим механическую систему, состоящую из тележки и груза D, в произвольном положении. Изобразим действующие на систему внешние силы: силы тяжести Р1 и Р2 и реакции плоскости Чтобы определить U, воспользуемся теоремой об изменении количества движения системы Q в проекции на ось х. Так как все действующие на систему внешние силы вертикальны (рис. Д2), то
Для рассматриваемой механической системы
Для определения VDx рассмотрим движение груза D как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня А D вокруг оси А), а движение самой тележки – переносным. Тогда
Но Вектор Изобразив этот вектор на рисунке Д2 с учетом знака
(В данной задаче величину При найденном значении VDx равенство (2), если учесть, что Ux=U, примет вид
Постоянную интегрирования С1 определим по начальным условиям: при t0 =0 U=U0. Подстановка этих значенийв уравнение (5) дает
Отсюда находим следующую зависимость скорости U от времени:
Подставив сюда значения соответствующих величин, находим искомую зависимость U от t. О т в е т:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

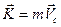 (1)
(1) на оси координат:
на оси координат: :
:  ;
;  (2)
(2) .
. .
. (3)
(3) ;
;  :
:  (4)
(4)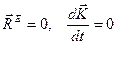
 . (5)
. (5) из первого уравнения (4)
из первого уравнения (4) откуда
откуда
 , а на рисунке 4-9 желоб –окружность радиуса R= 0,8 м и при движении груза угол
, а на рисунке 4-9 желоб –окружность радиуса R= 0,8 м и при движении груза угол  изменяется по закону
изменяется по закону  . В таблице Д2 эти зависимости даны отдельно для рисунков 0 и 1, для рис. 2 и 3 и.т.д., где S- выражено в метрах, φ- в радианах, t - в секундах.
. В таблице Д2 эти зависимости даны отдельно для рисунков 0 и 1, для рис. 2 и 3 и.т.д., где S- выражено в метрах, φ- в радианах, t - в секундах. , т.е. скорость плиты как функцию от времени.
, т.е. скорость плиты как функцию от времени.





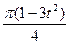










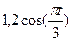



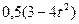














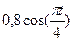


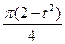
 с грузом D массой m2 на конце (Рис. Д2). В момент времени
с грузом D массой m2 на конце (Рис. Д2). В момент времени .
. рад (t- в секундах). О п р е д е л и т ь:
рад (t- в секундах). О п р е д е л и т ь:  . Проведем координатные оси Оху так, чтобы ось х была горизонтальна.
. Проведем координатные оси Оху так, чтобы ось х была горизонтальна. и теорема дает
и теорема дает

 (1)
(1)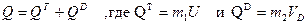 - количества движения тележки и груза D соответственно (U - скорость тележки, VD- скорость груза по отношению к осям Оху).Тогда из равенства (1) следует, что
- количества движения тележки и груза D соответственно (U - скорость тележки, VD- скорость груза по отношению к осям Оху).Тогда из равенства (1) следует, что (2)
(2) . (3)
. (3) .
.
 , найдем, что
, найдем, что . Окончательно из равенства (3) получим
. Окончательно из равенства (3) получим (4)
(4) можно найти другим путем, определив абсциссу
можно найти другим путем, определив абсциссу  груза D, для которой, как видно из рисунка Д2, получим
груза D, для которой, как видно из рисунка Д2, получим  .)
.) (5)
(5) и тогда из (5) получим
и тогда из (5) получим

 . (6)
. (6)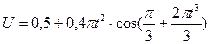 м/с.
м/с.





