
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра технической механики и гидравликиСодержание книги Поиск на нашем сайте
Кафедра технической механики и гидравлики
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Часть 2 (Динамика) контрольные задания и методические указания к выполнению курсовой (расчетно-графической) работы
Для студентов дневной и заочной форм обучения для специальностей:
110301-«Механизация сельского хозяйства» 110303-«Механизация переработки сельского хозяйства» 190603-«Сервис транспортных и технологических машин и оборудования в сельском хозяйстве» 190601-«Автомобили и автомобильное хозяйство» 270102-«Промышленное и гражданское строительство»
Санкт-Петербург-Пушкин Теоретическая механика: Часть 2 (Динамика) Контрольные задания и методические указания к выполнению курсовой (расчетно-графической) работы для студентов дневной и заочной форм обучения для специальностей: 110301-«Механизация сельского хозяйства», 110303-«Механизация переработки сельского хозяйства», 190603-«Сервис транспортных и технологических машин и оборудования в сельском хозяйстве», 190601-«Автомобили и автомобильное хозяйство», 270102-«Промышленное и гражданское строительство»
Составители: к.т.н. С.С. Соляник, д.т.н., профессор А.В. Соминич, д.т.н., профессор Б.И. Вагин
Рецензент: к.т.н. Н.В. Муханов
Задания и методические указания одобрены на заседании кафедры ТМиГ 12 октября 2011 г., протокол № 2 и рекомендованы к изданию методической комиссией факультета сельскохозяйственного строительства СПбГАУ, протокол №1 от 18 октября 2011 г.
Методические указания содержат: общие рекомендации по выполнению курсовой (расчетно-графической) работы; краткие теоретические сведения, необходимые для решения задач и успешной защиты работы; требования к оформлению и условные обозначения; примеры решения задач. За основу методических указаний взяты контрольные задания методических указаний под редакцией С.М. Тарга.
СОДЕРЖАНИЕ стр. Глава 1. Содержание раздела…………………………………………..4 Глава 2. Общие указания к выполнению контрольной работы……....5 Глава 3. Динамика………………………………………………………6 3.1. Теорема о движении центра масс………………………………....6 3.1.1. Задача Д1……………………………………………………….....7 3.1.2. Пример решения задачи Д1…………………………………….11 3.2. Теорема об изменения количества движения системы…………13 3.2.1. Задача Д2…………………………………………………………14 3.2.2. Пример решения задачи Д2……………………………………..15 3.3. Теорема об изменении кинетической энергии механической системы…………………………………………………………………..19 3.3.1. Задача Д3……………………………………………………….....21 3.3.2. Пример решения задачи Д3……………………………………...22 3.4. Принцип Германа-Эйлера-Даламбера для несвободной механи- ческой системы………………………………………………………….28 3.4.1. Задача Д 4…………………………………………………………29 3.4.2. Пример решения задачи Д 4……………………………………..29 Литература………………………………………………………………36 Приложения……………………………………………………………. 37
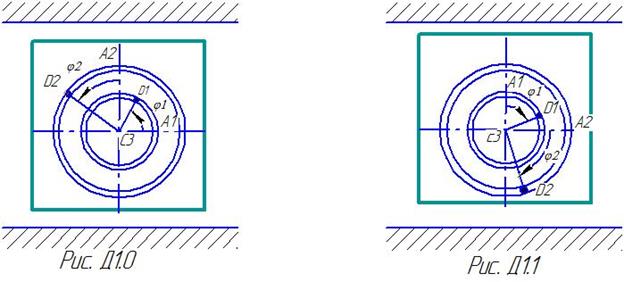
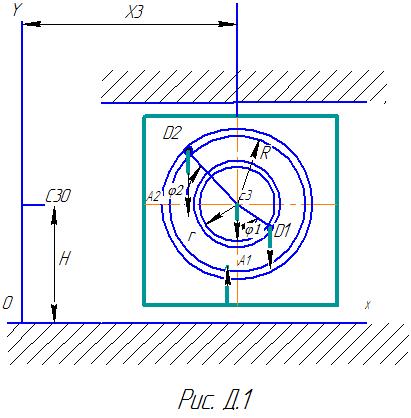
Глава 1. СОДЕРЖАНИЕ РАЗДЕЛА «Теоретическая механика» - одна из фундаментальных естественнонаучных дисциплин физико-математического цикла. На материале теоретической механики базируются дисциплины: «Сопротивление материалов», «Прикладная механика», «Теория машин и механизмов», «Детали машин», «Строительная механика», «Гидравлика», а также большое число специальных инженерных дисциплин. Теоретическая механика делится на три раздела: статику, кинематику и динамику. Статика изучает условия, при которых механическое воздействие тел не нарушает их относительного покоя или равномерного прямолинейного поступательного движения. Кинематика изучает движение объектов с геометрической точки зрения, то есть без учета их масс и сил, приложенных к ним. Динамика изучает движение материальных объектов с учетом действующих на них сил. В результате изучения теоретической механики студент должен знать: ДИНАМИКА Введение в динамику. Предмет динамики. Основные понятия и определения: масса, материальная точка, сила. Силы, зависящие от времени, от положения точки и от ее скорости. Законы классической механики или законы Галилея-Ньютона. Инерциальная система отсчета. Задачи динамики. Динамика точки. Решение первой и второй задачи динамики. Дифференциальные уравнения движения свободной и несвободной материальной точки в декартовой системе координат. Уравнения в проекциях на оси координат. Две основные задачи динамики для материальной точки. Решение первой задачи динамики. Решение второй задачи динамики. Прямолинейные колебания точки. Свободные колебания материальной точки. Амплитуда, начальная фаза, частота и период колебаний. Затухающие колебания материальной точки. Вынужденные колебания материальной точки. Явление резонанса. Введение в динамику. Механическая система. Силы внутренние и внешние. Свойства внутренних сил системы. Масса системы. Центр масс; радиус –вектор и координаты центра масс. Моменты инерции. Момент инерции тела относительно оси; радиус инерции. Теорема о моментах инерции относительно параллельных осей или теорема Гюйгенса. Примеры вычисления моментов инерции некоторых однородных тел. Общие теоремы динамики Теорема о движении центра масс. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс механической системы. Закон сохранения движения центра масс. Теорема об изменении количества движения. Количество движения материальной точки. Элементарный импульс силы. Импульс силы за конечный промежуток времени. Теорема об изменении количества движения материальной точки в дифференциальной и конечной формах. Закон сохранения количества движения механической системы. Теорема об изменении момента количества движения. Момент количества движения материальной точки относительно центра и относительно оси. Теорема об изменении момента количества движения. Закон сохранения кинетического момента механической системы. Теорема об изменении кинетической энергии. Кинетическая энергия материальной точки. Работа силы. Работа силы тяжести, силы упругости и силы тяготения. Кинетическая энергия механической системы. Глава 3. ДИНАМИКА ЗАДАЧА Д1 Механическая система состоит из грузов D1 массой m1=2 кг, D2 массой m2=6 кг и из прямоугольной вертикальной плиты массой m3=12 кг, движущийся вдоль горизонтальных направляющих (рис. Д.1.0-Д.1.9, табл. Д1). В момент времени t0 =0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r=0,4 м и R=0,8 м. При движении грузов угол Считая грузы материальными точками и пренебрегая всеми сопротивлениями, определить закон изменения со временем величины, указанной в таблице в столбце «Найти», т.е. Указания: Задача Д 1- на применение теоремы о движении центра масс. При этом для определения Таблица Д1
Пример решения задачи Д1.
Механическая система состоит из грузов D1 массой m1 и D2 массой m2 и из прямоугольной вертикальной плиты массой m3, движущийся вдоль горизонтальных направляющих (рис. Д1). В момент времени t0 =0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r и R по законам Д а н о: m1 =6 кг, m2 =8 кг, m3 =12 кг, r=0,6 м, R=1,2 м, Решение. Рассмотрим механическую систему, состоящую из плиты и грузов D1 и D2, в произвольном положении (рис. Д 1). Изобразим действующие на систему внешние силы: силы тяжести Р1, Р2, Р3 и реакцию направляющих N. Проведем координатные оси Оху так, чтобы ось у проходила через точку С30, где находится центр масс плиты в момент времени t0 =0. а) Определения перемещения х3. Для определения Получим
так как Проинтегрировав уравнение (1), найдем, что Интегрируя уравнение
т.е. центр масс системы вдоль оси Ох перемещаться не будет. Определим значение
В соответствии с равенством (2) координаты центра масс хс всей системы в начальном и произвольном положении будут равны. Следовательно, учитывая, что при
Отсюда получаем зависимость от времени координаты хс. О т в е т: б) Определение реакции N. Для определения
Отсюда получим, учтя, что
По формуле определяющей ординату ус центра масс системы,
или Продифференцировав обе части этого равенства два раза по времени, найдем
Подставив это значение О т в е т:
ЗАДАЧА Д2 Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1 =18 кг, движущейся вдоль горизонтальных направляющих, и груза D массой m2 =6 кг (рис. Д2.0-Д2.9, табл. Д2). В момент времени t0 =0, когда скорость плиты U0 =2 м/с, груз под действием внутренних сил начинает двигаться по желобу плиты. На рис 0-3 желоб КЕ прямолинейный и при движении груза расстояние S =АД изменяется по закону Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить зависимость Указания. Задача Д2 на применение теоремы об изменении количества движения системы. При решении составить уравнение, выражающее теорему, в проекции на горизонтальную ось.
Таблица Д 2
3.2.2. Пример решения задачи Д2. В центре тяжести А тележки массой m1, движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень А D длиной t0 =0, когда скорость тележки U=U0 стержень А D начинает вращаться вокруг оси А по закону Д а н о: m1 =24 кг, m2 =12 кг, U0 =0,5 м/с, Решение. Рассмотрим механическую систему, состоящую из тележки и груза D, в произвольном положении. Изобразим действующие на систему внешние силы: силы тяжести Р1 и Р2 и реакции плоскости Чтобы определить U, воспользуемся теоремой об изменении количества движения системы Q в проекции на ось х. Так как все действующие на систему внешние силы вертикальны (рис. Д2), то
Для рассматриваемой механической системы
Для определения VDx рассмотрим движение груза D как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня А D вокруг оси А), а движение самой тележки – переносным. Тогда
Но Вектор Изобразив этот вектор на рисунке Д2 с учетом знака
(В данной задаче величину При найденном значении VDx равенство (2), если учесть, что Ux=U, примет вид
Постоянную интегрирования С1 определим по начальным условиям: при t0 =0 U=U0. Подстановка этих значенийв уравнение (5) дает
Отсюда находим следующую зависимость скорости U от времени:
Подставив сюда значения соответствующих величин, находим искомую зависимость U от t. О т в е т:
Примеры вычисления работы сил 1. Сумма работ внутренних сил системы в общем случае отлична от нуля. 2. Если материальная система представляет собой абсолютно твердое тело, то сумма работ внутренних сил равна нулю. 3. Работа любой силы равна нулю, если сила приложена в неподвижной точке, скорость которой равна нулю в данный момент времени. 4. Работа внутренних сил натяжений гибких нерастяжимых тросов, канатов и т.п. равна нулю. 5. Работа силы тяжести равна произведению веса материальной системы на вертикальное перемещение центра масс, взятому со знаком «плюс», если центр масс опускается, и со знаком «минус», если центр масс поднимается: А=± Mghc, где М – масса материальной системы, кг; hc – вертикальное перемещение центра масс, м; g – ускорение свободного падения, м/с2. 6. Работа силы, приложенной к вращающемуся вокруг оси абсолютно твердому телу, равна: А=± MП(φ-φ0), где MП - момент пары сил, приложенной к телу, Нм; φ-φ0 – значение конечного угла поворота тела. 7. Работа силы трения: А= - Fтр·S, где S - перемещение, м. Работа силы трения всегда отрицательна. 8. Работа сил упругости пружины: А=0,5с∙(λ20 - λ21), где с - коэффициент жесткости пружины; λ - удлинение пружины, м. Работа положительна при λ0> λ1 и отрицательна при λ0< λ1.
ЗАДАЧА Д3 Пример решения задачи Д -3 Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3, радиусом инерции ρ3 относительно оси вращения, блока 4 радиуса R4 и подвижного блока 5 (коэффициент трения грузов о плоскость равен f).Тела системы соединены нитями, намотанными на шкив 3. К центру блока 5 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления. Дано: m1=0 кг, m2=5 кг, m3=6 кг, m4=0 кг, m5=4 кг, R3=0,3 м, r3= 0,1 м, ρ3=0,2 м, f=0,1, с=240 Н/м, М=0,6 Нм, F=80(3+2S)H, s1=0,2 м. Определить: vc5 в тот момент, когда s= s1.
Решение: 1.Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 2, 3, 5 и невесомых тел 1 и 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные F, Fупр, Р2, Р3, Р5, Fтр2, момент сопротивления М, натяжение нити S5 и реакции связей N2 , N3, N4 .
Рис. Д.3 2. Для определения vc5 воспользуемся теоремой об изменении кинетической энергии: Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями, работа внутренних сил равна нулю. В начальном положении все элементы механизма находились в покое, скорости всех тел были равны нулю, поэтому Т0=0. 3. Кинетическая энергия системы равна сумме энергий всех тел системы: Т= Т2+ Т3+ Т5. 4. Выполним кинематический анализ: - тело 2 движется поступательно; - тело 3 вращается вокруг неподвижной оси; - тело 5 участвует в плоскопараллельном движении. Исходя из этого, кинетическая энергия системы может быть представлена выражением:
5. Кинетическая энергия Т, которую получила система после того, как груз переместился вдоль наклонной плоскости на расстояние s1, зависит от искомой скорости vc5. Поэтому все скорости, входящие в выражение кинетической энергии данной механической системы, выразим через скорость vc5. 6. Поскольку грузы 1 и 2 связаны нерастяжимой нитью, то их скорости равны. В свою очередь эта нерастяжимая нить перекинута через малый обод шкива 3, следовательно: v1= v2= vА, где vА – любая точка обода радиуса r3 шкива 3. 7. Линейные скорости шкива 2 и блока 5 зависят от одной угловой скорости ω3: v2= ω3r3, v5= ω3R3. 8. Поскольку точка К5 является мгновенным центром скоростей для блока 5 (он как бы «катится» по участку нити К5L), то v5=2vc5. Тогда:
9. Осевые моменты инерции подвижного блока 5 и ступенчатого шкива 3 определяется выражениями:
10. Выполнив подстановку всех приведенных выше значений в выражение кинетической энергии для заданной механической системы, получим:
11. Находим работу всех действующих внешних сил при перемещении, которое будет иметь система, когда груз 1 пройдет путь s1=0,2 м. Введем следующие обозначения: s2 – перемещение груза 2 (s2=s1); φ3 – угол поворота шкива 3; h5 – перемещение центра масс блока 5; λ0, λ1 –начальное и конечное удлинение пружины. Сумма работ всех внешних сил равна:
Работы остальных сил равны нулю: - точка К5 – мгновенный центр скоростей, поэтому работа силы натяжения нити S5 равна нулю; - реакция опоры N2 перпендикулярна перемещению груза 2, а поэтому рабо- ты не совершает; - реакции N3, N4, приложенные в неподвижных точках, не совершают работы. По условию задачи λ0=0, тогда λ1 = sc5 – перемещение конца пружины. Выразим величины sc5 и φ3 через заданное перемещение s1. Зависимость между перемещениями такая же, как между соответствующими им скоростями: 12. Поскольку v5=v3=ω3R3 и vc5=0,5v5, то vc5=0,5ω3R3. Следовательно, λ1 = sc5=0,5φ3R3=0,5(s1R3)/r3. 13. При найденных значениях φ3 и λ1 получим выражение для подсчета суммы работ всех внешних сил, действующих на механическую систему:
14. Кинетическую энергию приравниваем к работе:
= Подставив в полученное выражение известные численные значения заданных величин, найдем искомую скорость vc5. Ответ: vc5 = 2,10 (м/c).
Таблица Д-3
Рис.Д3.0 Д.3.1.
Рис. Д3.2 Рис.Д 3.3.
Рис Д 3.4 Рис.Д.3.5.
Рис.Д 3.6. Рис. Д 3.7
Рис. Д.3.8 Рис.Д.3.9. ЗАДАЧА Д 4 Вертикальный вал АК(рис. Д4.0-Д4.8), вращающийся с постоянной угловой скоростью ω=10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д4 в столбце 2 (АВ=ВD=DЕ=ЕК=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m=10 кг, состоящий из частей 1 и 2 (размеры стержней показаны на рисунках, где b=0,1 м, а их массы m1 и m2 пропорциональны длинам), а невесомый стержень длиной Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а=0,6 м Указания. Задача Д4- на применение к изучению движения системы принципа Даламбера. При решении задачи учесть, что когда силы инерции частиц тела (в данной задаче стержня) имеют равнодействующую Пример решения задачи Д 4. Вертикальный вал длиной 3а (АВ=ВD =DЕ=ЕК=а), закрепленный подпятником А и подшипником D (Рис. Д 4,а), вращается с постоянной угловой скоростью ω. К валу жестко прикреплен в точке Е ломаный однородный стержень массой m и длиной Д а н о:
О п р е д е л и т ь: реакции подпятника А и подшипника D, пренебрегая весом вала. Решение: 1. Изображаем (с учетом заданных углов) и прикрепленные к нему в точках В и Е стержни (рис. Д4, б). Массы и веса частей 1 и 2 ломаного стержня пропорциональны длинам этих частей и соответственно равны
2. Для определения исходных реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси Аху так, чтобы стержни лежали в плоскости ху, и изобразим действующие на систему силы: активные силы – силы тяжести P1, P2, P3 и реакции связей – составляющие реакции подпятника ХА, УА и реакцию цилиндрического подшипника RD. Согласно принципу Даламбера, присоединим к этим силам силы инерции элементов однородного ломаного стержня и груза, считая его материальной точкой. Так как вал вращается равномерно, то элементы стержня имеют только нормальные ускорения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.255 (0.013 с.) |

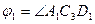 изменяется по закону
изменяется по закону  , а угол
, а угол  по закону
по закону  . В табл. Д.1 эти зависимости даны отдельно для рис.0-4 и 5-9, где φ -выражено в радианах t –в секундах.
. В табл. Д.1 эти зависимости даны отдельно для рис.0-4 и 5-9, где φ -выражено в радианах t –в секундах. и
и  , где x3- координата центра С3 плиты (зависимость
, где x3- координата центра С3 плиты (зависимость 






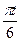
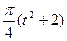





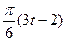

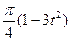











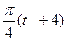





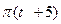





 рад,
рад,  рад (t-в секундах). О п р е д е л и т ь:
рад (t-в секундах). О п р е д е л и т ь:  или
или  (1)
(1) , поскольку все действующие на систему внешние силы вертикальны.
, поскольку все действующие на систему внешние силы вертикальны. , т.е. проекция скорости центра масс системы на эту ось есть величина постоянная. Так как в начальный момент времени
, т.е. проекция скорости центра масс системы на эту ось есть величина постоянная. Так как в начальный момент времени 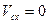 , то С1=0.
, то С1=0.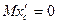 , получим
, получим (2)
(2) . Из рисунка Д1 видно, что в произвольный момент времени абсциссы грузов равны соответственно
. Из рисунка Д1 видно, что в произвольный момент времени абсциссы грузов равны соответственно  ,
,  . Так как по формуле, определяющей координату хс центра масс системы,
. Так как по формуле, определяющей координату хс центра масс системы,  , то
, то . (3)
. (3)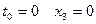 , получим
, получим (4)
(4)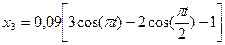 м, где t –в секундах.
м, где t –в секундах.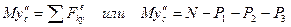 . (1)
. (1)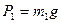 , и.т.д.:
, и.т.д.: . (2)
. (2)
 получим
получим

 .
. ;
; .
.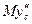 в уравнение (2), определим искомую зависимость N от t.
в уравнение (2), определим искомую зависимость N от t. , где t –в секундах, N – в ньютонах.
, где t –в секундах, N – в ньютонах. , а на рисунке 4-9 желоб –окружность радиуса R= 0,8 м и при движении груза угол
, а на рисунке 4-9 желоб –окружность радиуса R= 0,8 м и при движении груза угол  изменяется по закону
изменяется по закону  . В таблице Д2 эти зависимости даны отдельно для рисунков 0 и 1, для рис. 2 и 3 и.т.д., где S- выражено в метрах, φ- в радианах, t - в секундах.
. В таблице Д2 эти зависимости даны отдельно для рисунков 0 и 1, для рис. 2 и 3 и.т.д., где S- выражено в метрах, φ- в радианах, t - в секундах. , т.е. скорость плиты как функцию от времени.
, т.е. скорость плиты как функцию от времени.





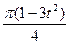










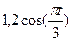



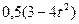













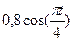


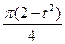
 с грузом D массой m2 на конце (Рис. Д2). В момент времени
с грузом D массой m2 на конце (Рис. Д2). В момент времени .
. рад (t- в секундах). О п р е д е л и т ь:
рад (t- в секундах). О п р е д е л и т ь:  . Проведем координатные оси Оху так, чтобы ось х была горизонтальна.
. Проведем координатные оси Оху так, чтобы ось х была горизонтальна.

 (1)
(1)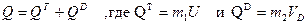 - количества движения тележки и груза D соответственно (U - скорость тележки, VD- скорость груза по отношению к осям Оху).Тогда из равенства (1) следует, что
- количества движения тележки и груза D соответственно (U - скорость тележки, VD- скорость груза по отношению к осям Оху).Тогда из равенства (1) следует, что (2)
(2) . (3)
. (3) .
.
 , найдем, что
, найдем, что . Окончательно из равенства (3) получим
. Окончательно из равенства (3) получим (4)
(4) можно найти другим путем, определив абсциссу
можно найти другим путем, определив абсциссу  груза D, для которой, как видно из рисунка Д2, получим
груза D, для которой, как видно из рисунка Д2, получим  .)
.) (5)
(5) и тогда из (5) получим
и тогда из (5) получим
 . (6)
. (6)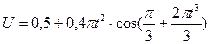 м/с.
м/с.



 , где
, где  - соответственно, сумма работ внешних и внутренних сил системы.
- соответственно, сумма работ внешних и внутренних сил системы. .
.

 .
. , где
, где


 =
=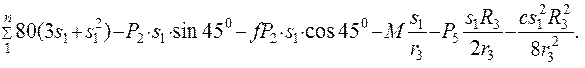




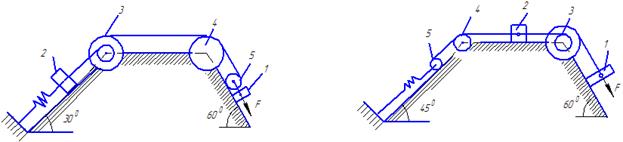
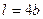 с точечной массой на конце m3 =3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы
с точечной массой на конце m3 =3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы  даны в столбцах 5-8.
даны в столбцах 5-8. , то численно
, то численно 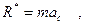 где
где  ускорение центра масс С тела, но линия действия силы
ускорение центра масс С тела, но линия действия силы  , состоящий из двух частей 1 и 2, а в точке В прикреплен невесомый стержень длиной
, состоящий из двух частей 1 и 2, а в точке В прикреплен невесомый стержень длиной 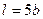 с точечной массой m 3 на конце; оба стержня лежат в одной плоскости.
с точечной массой m 3 на конце; оба стержня лежат в одной плоскости.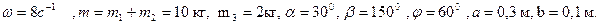
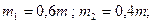
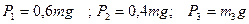 . (1)
. (1) , направленные к оси вращения, а численно
, направленные к оси вращения, а численно 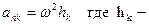 расстояния элементов от оси вращения. Тогда силы инерции
расстояния элементов от оси вращения. Тогда силы инерции 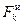 - будут направлены от оси вращения, а численно
- будут направлены от оси вращения, а численно ма
ма 


