
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о движении центра масс.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или главному вектору внешних сил. Уравнение (1) выражает теорему о движении центра масс системы, которая формулируется следующим образом: центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему. Проецируя обе части векторного равенства (1) на оси
где С л е д с т в и я из теоремы: 1.Если главный вектор внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Из уравнения (1) следует, что если 2. Если проекция главного вектора внешних сил на какую-либо неподвижную ось остается се время равной нулю, то проекция центра масс механической системы на эту ось или неподвижна, или движется равномерно. Из первого уравнения (2) следует, что если XE=0, то
Если при этом в начальный момент
т.е. координата х центра масс остается постоянной, а при Следствия из теоремы о движении центра масс системы выражает закон сохранения движения центра масс системы.
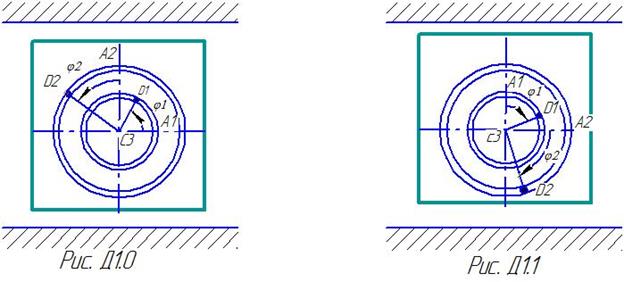
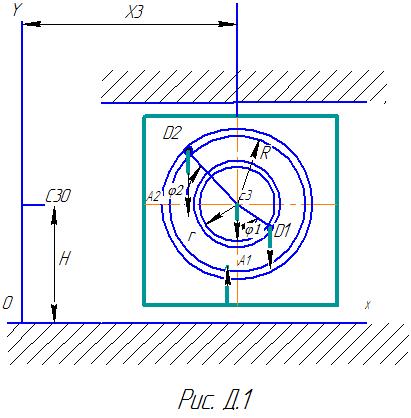
ЗАДАЧА Д1 Механическая система состоит из грузов D1 массой m1=2 кг, D2 массой m2=6 кг и из прямоугольной вертикальной плиты массой m3=12 кг, движущийся вдоль горизонтальных направляющих (рис. Д.1.0-Д.1.9, табл. Д1). В момент времени t0 =0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r=0,4 м и R=0,8 м. При движении грузов угол Считая грузы материальными точками и пренебрегая всеми сопротивлениями, определить закон изменения со временем величины, указанной в таблице в столбце «Найти», т.е. Указания: Задача Д 1- на применение теоремы о движении центра масс. При этом для определения Таблица Д1
Пример решения задачи Д1.
Механическая система состоит из грузов D1 массой m1 и D2 массой m2 и из прямоугольной вертикальной плиты массой m3, движущийся вдоль горизонтальных направляющих (рис. Д1). В момент времени t0 =0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r и R по законам Д а н о: m1 =6 кг, m2 =8 кг, m3 =12 кг, r=0,6 м, R=1,2 м, Решение. Рассмотрим механическую систему, состоящую из плиты и грузов D1 и D2, в произвольном положении (рис. Д 1). Изобразим действующие на систему внешние силы: силы тяжести Р1, Р2, Р3 и реакцию направляющих N. Проведем координатные оси Оху так, чтобы ось у проходила через точку С30, где находится центр масс плиты в момент времени t0 =0. а) Определения перемещения х3. Для определения Получим
так как Проинтегрировав уравнение (1), найдем, что Интегрируя уравнение
т.е. центр масс системы вдоль оси Ох перемещаться не будет. Определим значение
В соответствии с равенством (2) координаты центра масс хс всей системы в начальном и произвольном положении будут равны. Следовательно, учитывая, что при
Отсюда получаем зависимость от времени координаты хс. О т в е т: б) Определение реакции N. Для определения
Отсюда получим, учтя, что
По формуле определяющей ординату ус центра масс системы,
или Продифференцировав обе части этого равенства два раза по времени, найдем
Подставив это значение О т в е т:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.007 с.) |

 (1)
(1) получаем три уравнения в проекциях на оси координат:
получаем три уравнения в проекциях на оси координат: ;
;  ;
;  (2)
(2) - проекции силы
- проекции силы  - проекции главного вектора сил
- проекции главного вектора сил  на оси координат. Уравнения (2) представляют собой дифференциальные уравнения движения центра масс. Из уравнений (1) и (2) следует, что внутренние силы непосредственно не влияют на движение центра масс.
на оси координат. Уравнения (2) представляют собой дифференциальные уравнения движения центра масс. Из уравнений (1) и (2) следует, что внутренние силы непосредственно не влияют на движение центра масс. . При этом если начальная скорость
. При этом если начальная скорость  центра масс равна нулю, то центр масс находится в покое. Если же начальная скорость
центра масс равна нулю, то центр масс находится в покое. Если же начальная скорость  , то центр масс движется прямолинейно и равномерно с этой скоростью.
, то центр масс движется прямолинейно и равномерно с этой скоростью.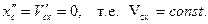
 , то
, то
 проекция центра масс на ось х движется равномерно.
проекция центра масс на ось х движется равномерно.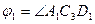 изменяется по закону
изменяется по закону  , а угол
, а угол  по закону
по закону  . В табл. Д.1 эти зависимости даны отдельно для рис.0-4 и 5-9, где φ -выражено в радианах t –в секундах.
. В табл. Д.1 эти зависимости даны отдельно для рис.0-4 и 5-9, где φ -выражено в радианах t –в секундах. и
и  , где x3- координата центра С3 плиты (зависимость
, где x3- координата центра С3 плиты (зависимость 






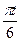
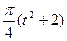





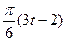

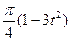











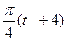





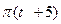





 рад,
рад,  рад (t-в секундах). О п р е д е л и т ь:
рад (t-в секундах). О п р е д е л и т ь:  или
или  (1)
(1) , поскольку все действующие на систему внешние силы вертикальны.
, поскольку все действующие на систему внешние силы вертикальны. , т.е. проекция скорости центра масс системы на эту ось есть величина постоянная. Так как в начальный момент времени
, т.е. проекция скорости центра масс системы на эту ось есть величина постоянная. Так как в начальный момент времени 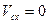 , то С1=0.
, то С1=0.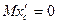 , получим
, получим (2)
(2) . Из рисунка Д1 видно, что в произвольный момент времени абсциссы грузов равны соответственно
. Из рисунка Д1 видно, что в произвольный момент времени абсциссы грузов равны соответственно  ,
,  . Так как по формуле, определяющей координату хс центра масс системы,
. Так как по формуле, определяющей координату хс центра масс системы,  , то
, то . (3)
. (3)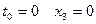 , получим
, получим (4)
(4)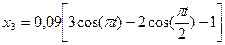 м, где t –в секундах.
м, где t –в секундах.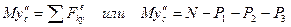 . (1)
. (1)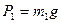 , и.т.д.:
, и.т.д.: . (2)
. (2)
 получим
получим

 .
. ;
; .
.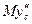 в уравнение (2), определим искомую зависимость N от t.
в уравнение (2), определим искомую зависимость N от t. , где t –в секундах, N – в ньютонах.
, где t –в секундах, N – в ньютонах.


