
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упр 1. Элементы кинематики материальной точки и вращательного движения абсолютно твердого тела.Содержание книги
Поиск на нашем сайте Лабораторные работы: Лаб. II № 4,7, 8,9 (можно 10 вместо 7) Лаб. IV № 16, 18(а, б), 28 Программа Валишев М.Г., Повзнер А.А., Курс общей физики Дополнительный учебник: Трофимова Т.И «Курс физики» Чертов А.Г., Воробьев А.А., Задачник по физике, 1988 Упр 1. Элементы кинематики материальной точки и вращательного движения абсолютно твердого тела. Определения кинематики: система отсчета, радиус-вектор Кинематика вращения твердого тела вокруг неподвижной оси. Угловая скорость Задачи (Чертов) В классе 1. 3, 6,16,18, 21, 29, 36, 48, 53 Дома 1.5, 9,10, 14, 22, 34, 49, 54 - 57
Упр 2. Динамика материальной точки и поступательного движения твердого тела Первый закон Ньютона, масса, сила. Второй закон Ньютона (уравнение движения). Силы в механике: сила упругости, сила трения, гравитационная сила и её составляющая сила тяжести. Третий закон Ньютона. Закон сохранения импульса для системы материальных точек как следствие законов Ньютона. Задачи: В классе 2.3, 7, 12, 18, 36, 38, 44, 47 Дома 2.5, 10, 19, 22, 37,39, 46, 50
Упр 3. Работа и энергия. Определение элементарной и полной работы. Кинетическая энергия. Потенциальная энергия поднятого и упруго деформированного тела. Консервативные силы и системы, связь консервативной силы с потенциальной энергией. Закон сохранения механической энергии как следствие законов Ньютона. Графическое представление энергии, потенциальные кривые (потенциальная яма и потенциальный барьер). Задачи об абсолютно упругом и неупругом ударах. Задачи: 2.58, 72, 73, 76, 78, 83, 86 Дома 2. 62, 75, 77, 79, 84, 87, 91
Упр.7 Распределение Максвелла и Больцмана Функция распределения. Распределение молекул по модулю скорости теплового движения в равновесном состоянии (функция Максвелла). Наиболее вероятная, среднеарифметическая и среднеквадратическая скорости молекул. Распределение молекул в поле силы тяжести (барометрическая формула). Распределение Больцмана. Степени свободы газовых молекул и принцип равнораспределения энергии теплового движения по степеням свободы. Энергия теплового движения в газе одно-, двух- и многоатомных молекул. Задача 1. Определить температуру газообразного азота, при которой скоростям молекул 300 м/с и 600 м/с, соответствуют одинаковые функции распределения. Задача 2. Найти скорость газообразного азота, при которой значение f(v) для температуры Т0 будет такой же, как и для температуры в n раз большей. Задачи:В классе 9. 28, 10.17, 10.16, 19, 26, 4, 9 Дома 10.18, 20, 28, 40, 5-7
Электромагнетизм Упр. 10. Закон Кулона. Теорема Гаусса. Расчет полей. Закон Кулона. Электростатическое поле. Напряженность. Поток вектора напряженности. Теорема Гаусса. Применение теоремы Гаусса для расчета поля равномерно заряженной плоскости, непроводящего шара, равномерно заряженных нити, цилиндра, пластины. В классе 13.2, 10, 20; 14., 11, 14, 23, 28 Дома 13. 3, 4, 8, 13, 18; 14. 3, 4, 10, 12, 16, 15, 25, 29, Тонкое проводящее кольцо радиуса R заряжено с линейной плотностью l = l0cosj, где l0 = const, j - азимутальный угол. Найти модуль напряженности электрического поля в центре кольца. I. Механика 1. Зависимость пройденного телом пути от времени дается уравнением S = B + 2Ct + Dt3, где B =6 м, C=3 м/с, D= - 0,5 м/с3 - постоянные величины. Определить момент времени, когда скорость тела будет равна нулю, а также значение ускорения в этот момент времени. 2. Камень брошен горизонтально со скоростью v0 =18 м/с. Найти нормальное an и тангенциальное at ускорения тела через время t = 1 с после начала движения. Каков радиус кривизны траектории в этой точке? 3. Камень, брошеный горизонтально, через время t = 0,5 с после начала движения имел скорость в 1,5 раза больше скорости v0 в момент бросания. С какой скоростью v0 был брошен камень? 4. Тело брошено со скоростью v0 = 14,7 м/с под углом a = 300 к горизонту. Найти нормальное an и тангенциальное at ускорения тела через время t = 1,25 с после начала движения. 5. Тело массой m = 1 кг движется прямолинейно, причем зависимость пройденного телом пути от времени дается уравнением S = A + Bt + Ct2—Dt3, где C =5 м/с2 и D =1 м/с3. Определите силу, действующую на тело в конце первой секунды движения. 6. Тело скользит по наклонной плоскости, образующей с горизонтом угол 7. Самолет поднимается и на высоте h = 5 км достигает скорости v = 360 км/ч. Во сколько раз работа A 1, совершаемая при подъеме против силы тяжести, больше работы A 2, идущей на увеличение скорости самолета? 8. Найти работу, которую надо совершить, чтобы увеличить скорость движения тела от 2 м/с до 8 м/с на пути в 15 м. На всем пути действует сила трения равная 3 Н. Масса тела – 1,5 кг. 9. С башни высотой 25 м горизонтально брошен камень со скоростью 20 м/с. Найти кинетическую и потенциальную энергию камня спустя 1,5 секунды после начала движения. Масса камня 0,1 кг. Сопротивлением воздуха пренебречь. 10. Автомобиль массой 3 т движется по наклонной плоскости вверх с постоянной скоростью. Найти силу тяги автомобиля, если угол наклонной плоскости 30°, а коэффициент трения 0,03. 11. Камень бросили под углом a = 60° к горизонту со скоростью v0 =14 м/с. Масса камня m = 0,2 кг. Сопротивлением воздуха пренебречь. Найти кинетическую и потенциальную энергию камня в высшей точке траектории. 12. Тело массы m =1 кг бросили вертикально вверх с поверхности земли с начальной скоростью ν =10 м/с. Работа силы сопротивления воздуха за все время движения тела составила Ас= -18 Дж. Определить с какой скоростью тело упало на землю. 13. Конькобежец массой 60 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. На какое расстояние откатится при этом конькобежец? Коэффициент трения коньков о лед 0,001. 14. Тело массой 0,3 кг, двигающееся со скоростью 5 м/с, сталкивается с неподвижным телом массой 0,7 кг. Считая удар абсолютно неупругим, найти: скорость тел после столкновения и работу неконсервативных сил за время удара. 15. Ядро массой 25 кг, двигаясь горизонтально со скоростью 300 м/с попадает в вагон с песком, который может свободно двигаться по рельсам и застревает в нем. Определить количество теплоты, выделившееся в результате этого, если масса вагона с песком 3 т. 16. Из орудия массой 5 т вылетает снаряд массой 100 кг. Кинетическая энергия снаряда при вылете 7,5 Мдж. Какую кинетическую энергию получает орудие вследствие отдачи. 17. Камень, пущенный по поверхности льда со скоростью 2 м/с, прошел до полной остановки расстояние 20,4 м. Найти коэффициент трения камня по льду, считая его постоянным. 18. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 19. Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости вращения диска от времени дается уравнением 20. Диск радиусом 20 см вращается согласно уравнению 21. Колесо, вращаясь равнозамедленно, за время t = 60 с уменьшило свою частоту с n 1 = 300 об/мин до n 2 = 180 об/мин. Найдите угловое ускорение e колеса и число оборотов N колеса за это время. 22. Колесо автомашины вращается равноускоренно. Сделав N = 50 полных оборотов, оно изменило частоту вращения от n1 = 4 c-1 до n2 = 6 c-1. Определите угловое ускорение колеса. 23. К ободу однородного диска радиусом R = 0,2 м приложена касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения M тр = 4,9 Н×м. Найти массу диска, если диск вращается с угловым ускорением e = 100 рад/с2. 24. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 10 кг. Найти момент инерции I барабана, если известно, что груз опускается с ускорением 2,04 м/c2. 25. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязаны грузики массой m1 = 100 г и m2 = 110 г. С каким ускорением будут двигаться грузики, если масса блока m = 400 г? Трение при вращении блока ничтожно мало. 26. К ободу диска массой m = 5 кг приложена касательная сила F = 20 Н. Какую кинетическую энергию будет иметь диск через t = 5 с после начала действия силы? 27. Маховик в виде диска массой 80 кг и радиусом 30 см находится в состоянии покоя. Определить работу внешних сил при сообщении маховику частоты вращения 12 об/с. 28. Колесо, вращаясь равнозамедленно, уменьшило за 1 мин частоту вращения от 300 об/мин до 180 об/мин. Момент инерции колеса 2 кг×м2. Найти угловое ускорение колеса; момент сил торможения; работу сил торможения. 29. Маховик в виде диска массой 80 кг и радиусом 30 см находится в состоянии покоя. Определить работу внешних сил при сообщении маховику частоты вращения 10 об/с; работу внешних сил в случае, когда диск при той же массе имел бы радиус в два раза больше. 30. Диск массой 3 кг катится без скольжения по горизонтальной плоскости со скоростью v = 4 м/c. Найти кинетическую энергию диска. 31. Мальчик катит обруч по горизонтальной дороге со скоростью 7,2 км/ч. На какое расстояние может вкатиться обруч на горку за счет своей кинетической энергии. Уклон горки равен 15 м на каждые 100 м пути. Трением пренебречь/ 32. Кинетическая энергия вала, вращающегося с частотой n = 5 об/c равна 60 Дж. Найдите момент импульса L вала. 33. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n1 = 10 об/мин. Человек массой M = 60 кг стоит при этом на краю платформы. С какой частотой n2 начнет вращаться платформа, если человек перейдет от края к центру платформы? Платформу считать однородным диском, а человека – точечной массой.
II. МКТ. Термодинамика 1. 12 г газа занимают объем V = 4×10–3 м3 при температуре t = 7 °C. После нагревания газа при постоянном давлении его плотность стала равна r = 6×10 –4 г/см3. До какой температуры нагрели газ? 2. Найти среднеквадратическую скорость молекул газа, плотность которого при давлении р = 10 5 Па равна r = 8,2×10 –2 кг/м3. Чему равна молярная масса этого газа, если значение плотности дано для температуры t = 17 °С? 3. В закрытом сосуде находится масса m = 28 г азота при давлении p1 = 100 кПа и температуре t = 270С. После нагревания давление в сосуде повысилось в 6 раз. До какой температуры был нагрет газ? Найдите объем сосуда и количество теплоты, сообщенное газу. 4. В сосуде объемом V = 4 л находятся 4 г углекислого газа (СО2) и 8 г закиси азота (N2O) при температуре 1270 С. Найти давление смеси газов в сосуде. 5. В баллоне вместимостью V = 25 л находится водород при температуре T = 290 К. После того как часть водорода израсходовали, давление в баллоне понизилось на Δр = 0,4 МПа. Определить массу израсходованного водорода. 6. В колбе вместимостью V = 100 см3 содержится некоторый газ при температуре T = 300 К. На сколько понизится давление р в колбе, если вследствие утечки из колбы выйдет N = 1020 молекул. 7. На какой высоте h давление воздуха составляет 80% от давления на уровне моря? Температуру воздуха считать постоянной и равной t =00С. 8. На какой высоте плотность водорода на 30% меньше его плотности на уровне моря? Температуру водорода считать постоянной и равной t =00С. 9. Трехатомный газ массой m = 1 кг и плотностью r = 2 кг/м3 находится под давлением p = 80 кПа. Найдите энергию теплового движения U молекул этого газа. 10. При изобарическом расширении двухатомного газа была совершена работа А = 164 Дж. Какое количество теплоты было сообщено газу при этом расширении? 11. Какую массу углекислого газа можно нагреть при p = const от температуры 200 С до температуры 1000 С количеством теплоты Q = 222 Дж? На сколько при этом изменится средняя кинетическая энергия одной молекулы? 12. При изотермическом расширении 14 г азота, находящегося при температуре 170С была совершена работа А = 960 Дж. Во сколько раз изменилось давление азота при расширении? 13. Работа изотермического расширения массы m = 10 г некоторого газа от объема V1 до объема V2 = 2 V1 оказалась равной A = 575 Дж. Найти среднюю квадратическую скорость молекул газа при этой температуре. 14. Баллон вместимостью 20 л содержит водород при температуре T1 = 300 К и давлении p1 = 0,4 МПа. Каковы будут температура T 2 и давление p 2, если газу сообщить количество теплоты Q = 6 кДж? 15. При изотермическом расширении 1 моль кислорода, имевшего температуру T = 300 К, газу было передано количество теплоты Q = 2 кДж. Во сколько раз увеличился объем кислорода? 16. Один моль одноатомного идеального газа, находящегося при давлении p 1 = 1,0×104 Па, адиабатически расширяется из состояния 1 в состояние 2, совершая работу А = 10 кДж. При этом его температура понизилась в 2 раза. Найти объемы V 1 и V 2 начального и конечного состояния, соответственно. 17. Объем V 1=7,5 л кислорода адиабатически сжимается до объема V 2=1 л, причем в конце сжатия установилось давление р 2=1,6 МПа. Под каким давлением р 1 находился газ до сжатия? 18. Количество n = 1кмоль азота, находящегося при нормальных условиях (температуре t 1 = 00С и давлении p1 = 0,1 МПа), расширяется адиабатически от объема V 1 до V 2 = 5 V 1. Найти приращение внутренней энергии газа и работу, совершенную газом при расширении. 19. Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=73,5 кДж. Температура нагревателя t 1=1000C, температура холодильника t 2=00 С. Найти КПД h цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику. 20. Тепловая машина, работающая по циклу Карно, за цикл получает от нагревателя количество теплоты Q1 = 2512 Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 300 К. Найти работу А, совершаемую машиной за один цикло, и количество теплоты Q2, отдаваемое холодильнику за цикл. 21. Азот массой m = 7 г изобарически расширился от объема V1 = 2 л до объема V2 = 6 л. Найти количество теплоты сообщенное азоту и изменение энтропии DS при этом процессе. 22. Во сколько раз следует изотермически увеличить объем 4 молей идеального газа, чтобы его энтропия испытала приращение D S = 23 Дж/ К? 23. Найти приращение D S энтропии при переходе массы m =8 г углекислого газа от объема V 1=10 л при температуре t1=800С к объему V 2=40 л при температуре t 2=3000С. 24. 16 г кислорода нагревается от температуры t1 = 500 С до t2 = 1500 С. Найти приращение энтропии, если нагревание происходит:1) изохорически; 2) изобарически. 25. Найти приращение энтропии при изотермическом расширении 6г гелия от давления p1 = 100 кПа до давления p2 = 50 кПа. 26. Кислород массой 2 кг увеличил свой объем в 5 раз. Найти изменение энтропии, если расширение проходило а) изотермически; б) адиабатно. 27. В результате нагревания m =22 г азота его абсолютная температура увеличилась в n=1,2 раза, а энтропия увеличилась на D S =4,19 Дж/К. При каких условиях производилось нагревание (при постоянном объеме или при постоянном давлении)? 28. Гелий массой m =1,7 кг адиабатически расширили в 3 раза и затем изобарически сжали до первоначального объема. Найти приращение энтропии DS при этом процессе. 29. Найти приращение DS энтропии при превращении массы m =100 г льда (t = -100C) в воду с температурой t =400С. Удельная теплоемкость льда 2100 Дж/ кг*К, удельная теплоемкость воды 4200 Дж/ кг*К, удельная теплота плавления льда = 335кДж/К. 30. Найти приращение DS энтропии при превращении массы m =1 г воды (t = 00C) в пар (tп = 1000С). Удельная теплоемкость воды св=4200 Дж/ кг*К, удельная теплота парообразования r = 2,26 МДж/К.
III. Электростатика 1. Два разноименных и равных по величине заряда q =2 нКл расположены в вершинах при острых углах равнобедренного прямоугольного треугольника на расстоянии
3. На рисунке AA- заряженная бесконечная плоскость с поверхностной плотностью заряда s = 40 мкКл/м2 и В – одноименно заряженный шарик массой 1г и зарядом q = 1 нКл. Какой угол a с плоскостью АА образует нить, на которой висит шарик?
4. Две бесконечно длинные равномерно заряженные нити с линейной плотностью заряда t=5,0*10-5 Кл/м расположены на расстоянии а =0,1 м друг от друга. Найти напряженность электрического поля в точке, находящейся на расстоянии b =0,1 м от каждой нити. 5. Две параллельные металлические пластины, расположенные в диэлектрике (ε =2,2), обладают поверхностной плотностью заряда σ1 = 3 мк Кл/м2 и σ2 = 2 мкКл/м2. Найти напряженность электрического поля внутри и вне пластин. 6. Найти величину и направление напряженности электрического поля, созданного точечным зарядом q = 18*10-8 Кл и бесконечно длинной заряженной нитью с линейной плотностью заряда t=0,5*10-5 Кл/м, в точке, удаленной от заряда на a= 4,0 см, от нити на расстояние b =3,0 см. Расстояние между зарядом и нитью с = 5,0 см. 7. С какой силой F l (на единицу длины) отталкиваются две одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда t= 5 мкКл/м, находящиеся на расстоянии r 1 =30 мм друг от друга? Какую работу Аl (на единицу длины) надо совершить, чтобы сблизить нити до расстояния r 2 =10 мм? 8. Два шарика одинакового радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются, Какой заряд надо сообщить шарикам, чтобы сила натяжения стала равной Т = 98 мН? Расстояние от точки подвеса до центра шарика l = 10 см; а масса каждого шарика m = 4 г. 9. С какой силой Fl электрическое поле заряженной бесконечной плоскости действует на единицу длины заряженной бесконечно длинной нити, помещенной в это поле? Линейная плотность заряда на нити l = 5 мкКл/м и поверхностная плотность заряда на плоскости s = 30 мкКл/м2. 10. Найти силу, действующую на заряд q = 2 нКл, если заряд помещен на расстоянии r = 4 см от заряженной нити с линейной плотностью заряда l = 0,3 мкКл/м. 11. Расстояние между двумя точечными зарядами q 1= -0,33 мкКл и q 2= 0,33 мкКл равно а =10 см. Найти напряженность поля в точке, находящейся на перпендикуляре, восстановленном к середине линии, соединяющей лба заряда на расстоянии b =10 см от нее. 12. Найти силу, действующую на заряд q = 3 нКл, если заряд помещен на расстоянии r = 2 см от заряженной нити с линейной плотностью заряда l = 0,1 мкКл/м. 13. Около заряженной бесконечно протяженной плоскости находится точечный заряд q = 7,0*10-7 Кл. Под действием поля заряд перемещается по силовой линии на расстояние D r = 2 см, при этом силы поля совершают работу А = 5,0*10-6 Дж. Найти поверхностную плотность заряда на плоскости. 14. Какая работа А совершается при перенесении точечного заряда q = 10 нКл из бесконечности в точку, находящуюся на расстоянии r = 0,5 см от поверхности шара радиусом R = 1 см с поверхностной плотностью заряда s = 10 мкКл/м2. 15. Два шарика с зарядами q 1 =7,0 нКл и q 2 =1,4 нКл находятся на расстоянии r 1 =40 см. Какую работу надо совершить, чтобы сблизить их до расстояния r 2 =25 см? 16. Найти потенциал j точки поля, находящейся на расстоянии r = 12 см от поверхности заряженного шара радиусом R = 2 см, если потенциал шара j0 = 300 В. 17. Шарик, заряженный до потенциала j = 792 В, имеет поверхностную плотность заряда s = 333 нКл/м2. Найдите радиус шарика. 18. Шарик с массой m = 1,5 г и зарядом q = 15 нКл перемещается из точки 1, потенциал которой j1 = 600 В, в точку 2, потенциал которой j2 = 0. Найти его скорость в точке 1, если в точке 2 она стала равной V 2 = 30 см/с. 19. Электрон с энергией W k= 6,4×10-17 Дж (в бесконечности) движется вдоль линии напряженности по направлению к поверхности металлической заряженной сферы радиусом R =10 см. Определить минимальное расстояние rmin, на которое приблизится электрон к поверхности сферы, если ее заряд Q = -10 нКл. 20. На расстоянии r 1 = 20 см от бесконечно длинной заряженной нити находится точечный заряд q= 7*10-10 Кл. Под действием поля заряд перемещается до расстояния r 2 = 40 см. При этом силами поля совершается работа А = 5,0*10-6 Дж. Найти линейную плотность заряда нити t. 21. Электрическое поле образовано положительно заряженной бесконечно длинной нитью. Двигаясь под действием этого поля от точки, находящейся на расстоянии r 1 = 1 см от нити, до точки r 2 = 4 см, a - частица изменила свою скорость от V 1 = 2×105 м/с до V 2 = 3×106 м/с. Найти линейную плотность заряда t на нити. (q a = 3,2×10-19 Кл, m a = 6,69×10-27 кг). 22. Пластины плоского конденсатора площадью S =0,01 м2 каждая притягиваются друг к другу с силой F = 40 мН. Пространство между пластинами заполнено стеклом (e=6). Найти заряды q пластин, напряженность Е поля между пластинами и объемную плотность энергии w поля. 23. Электрическое поле образовано двумя параллельными пластинами, находящимися на расстоянии d =2 см друг от друга. К пластинам приложена разность потенциалов U =140 В. Какую скорость получит электрон под действием поля, пройдя по линии напряженности расстояние s =5 мм? 24. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобретает скорость v = 106 м/с. Расстояние между пластинами d = 5,3 мм. Найти разность потенциалов U между пластинами, напряженность Е электрического поля конденсатора и поверхностную плотность заряда s на его пластинах. 25. Электрон влетает в плоский горизонтально расположенный конденсатор параллельно его пластинам со скоростью u0 = 107 м/c. Напряженность поля в конденсаторе E = 10 кВ/м, длина конденсатора l = 4 см. Найти модуль и направление скорости электрона при вылете его из конденсатора. 26. Протон влетает в плоский горизонтально расположенный конденсатор параллельно его пластинам со скоростью u0 =1,4 105 м/c. Напряженность поля в конденсаторе E = 3,7 кВ/м, длина конденсатора l = 16 см. Во сколько раз скорость протона при вылете из конденсатора будет дольше его начальной скорости? 27. Между пластинами плоского конденсатора, находящимися на расстоянии d = 5 мм друг от друга приложена разность потенциалов U = 150 В. К одной из пластин прилегает плоскопараллельная пластинка фарфора толщиной d 1 = 3 мм. Найти напряженности E 1 и E 2 в фарфоре и воздухе. Диэлектрическая проницаемость фарфора e = 6. 28. Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов. Его энергия при этом W = 20 мкДж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, А =70 мкДж. Найти диэлектрическую проницаемость e диэлектрика. 29. Площадь пластин плоского воздушного конденсатора S = 0,01 м2, расстояние между ними d 1 = 1 мм. К пластинам приложена разность потенциалов U =100 В. Пластины раздвигаются до расстояния d 2=25 мм. Найти энергии W 1 и W 2 до и после раздвижения пластин если источник напряжения перед раздвижением: а) не отключается, б) отключается 30. Площадь пластин плоского воздушного конденсатора S =0,02 м2, расстояние между ними d = 5мм. Какая разность потенциалов была приложена к пластинам конденсатора, если известно, что при разряде конденсатора выделилось Q =6,2 мДж тепла? 31. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r = 10 см каждая. Расстояние между пластинами d 1 = 1 см. Конденсатор зарядили до разности потенциалов U = 1 кВ и отключили от источника питания. Какую работу нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d 2 = 3,5 см?
IV. Постоянный ток. 1. Найдите падение напряжения U на медном проводе длиной l = 300 м и диаметром d = 1,5 мм, если ток в нем I = 2А. Удельное сопротивление меди r = 17 нОм×м. 2. Какова длина l медного проводника, если при разности потенциалов U = 0,34В на его концах, плотность тока в нем j = 10 А/мм2. Удельное сопротивление меди r = 17 нОм×м. 3. Вольфрамовая нить электрической лампочки при t 1 = 200 С имеет сопротивление R 1 = 35,8 Ом. Какова будет температура лампочки, если при включении в сеть с напряжением U = 120 В по нити идет ток I = 0,33A? Температурный коэффициент сопротивления вольфрама a = 4,6×10-3 К-1. 4. По проводнику диаметром d = 1 мм течет ток силой I = 3,14 А. Концентрация свободных электронов в проводнике n = 2,5×1028 м-3, заряд электрона q = 1,6×10-19 Кл. Какова средняя скорость направленного движения электронов в проводнике? 5. Сколько электронов пройдет за время t = 32 с через поперечное сечение провода диаметром d = 2 мм, длиной l = 10 м при разности потенциалов на его концах U = 3,2 В? Удельное сопротивление алюминия r = 28 нОм×м, заряд электрона e = 1,6×10-19 Кл.
6. Два одинаковых элемента e1 = e2 = 2 В, r1 = r2 = 0,5 Ом. Найти токи I1 и I2, текущие через сопротивления R1 = 0,5 Ом, R2 = 1,5 Ом, а также ток I через элемент с e1.
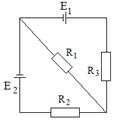
7. Элементы питания имеют ЭДС e1 = 2 В, e2 = 4 В и e3 = 6 В, сопротивления R1 = 4 Ом, R2 = 6 Ом, R3 = 8 Ом. Найти токи во всех участках цепи.
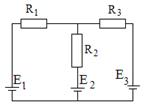
8. ЭДС элементов e1 = 2,1 В и e2 = 1,9 В, сопротивления R1= 45 Ом, R2= 10 Ом, R3= 10 Ом. Найти токи во всех участках цепи.
Две батареи аккумуляторов (e1=10 В, r1=1 Ом, e2=8 В, r2=2 Ом) и реостат (R = 6 Ом) соединены так как показано на рисунке. Найти силу тока в батареях и реостате.
R3= 300 Ом, сопротивление вольтметра Rv= 2 кОм. Какую разность потенциалов показывает вольтметр?
Лабораторные работы: Лаб. II № 4,7, 8,9 (можно 10 вместо 7) Лаб. IV № 16, 18(а, б), 28 Программа Валишев М.Г., Повзнер А.А., Курс общей физики Дополнительный учебник: Трофимова Т.И «Курс физики» Чертов А.Г., Воробьев А.А., Задачник по физике, 1988 Упр 1. Элементы кинематики материальной точки и вращательного движения абсолютно твердого тела. Определения кинематики: система отсчета, радиус-вектор Кинематика вращения твердого тела вокруг неподвижной оси. Угловая скорость Задачи (Чертов) В классе 1. 3, 6,16,18, 21, 29, 36, 48, 53 Дома 1.5, 9,10, 14, 22, 34, 49, 54 - 57
|
||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.027 с.) |

 , скорость
, скорость  , ускорение
, ускорение 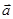 и его составляющие тангенциальное
и его составляющие тангенциальное  и нормальное
и нормальное  ускорение при криволинейном движении материальной точки. Связь нормального ускорения со скоростью и радиусом кривизны траектории.
ускорение при криволинейном движении материальной точки. Связь нормального ускорения со скоростью и радиусом кривизны траектории. и угловое ускорение
и угловое ускорение  . Связь между угловыми и линейными кинематическими величинами.
. Связь между угловыми и линейными кинематическими величинами.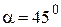 . Зависимость пройденного телом пути от времени дается уравнением
. Зависимость пройденного телом пути от времени дается уравнением 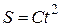 , где
, где  м/с2. Найти коэффициент трения m тела о плоскость.
м/с2. Найти коэффициент трения m тела о плоскость. , где B = 1,0 рад/c, C = 1,0 рад/c2, D = 1,0 рад/c3. Найти радиус R колеса, если известно, что к концу второй секунды движения, для точек, лежащих на ободе колеса, нормальное ускорение an = 3,46 м/c2.
, где B = 1,0 рад/c, C = 1,0 рад/c2, D = 1,0 рад/c3. Найти радиус R колеса, если известно, что к концу второй секунды движения, для точек, лежащих на ободе колеса, нормальное ускорение an = 3,46 м/c2. , где С = 8 рад/с2. Найти касательную силу, приложенную к ободу диска. Трением пренебречь.
, где С = 8 рад/с2. Найти касательную силу, приложенную к ободу диска. Трением пренебречь.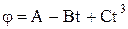 , где А = 3,0 рад/c, B = 1,0 рад/c, C = 0,1 рад/c3 . Определить тангенциальное a τ, нормальное an и полное a ускорения точек на окружности диска для момента времени t = 10 с.
, где А = 3,0 рад/c, B = 1,0 рад/c, C = 0,1 рад/c3 . Определить тангенциальное a τ, нормальное an и полное a ускорения точек на окружности диска для момента времени t = 10 с.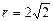 см друг от друга. Определить с какой силой эти заряды действуют на третий заряд q 0= 1 нКл, расположенный в третьей вершине треугольника.
см друг от друга. Определить с какой силой эти заряды действуют на третий заряд q 0= 1 нКл, расположенный в третьей вершине треугольника.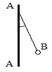 2. Найти напряженность электрического поля в точке, лежащей посередине между точечными зарядами q 1= -8 нКл и q 2= 4 нКл. Расстояние между зарядами r = 10 см.
2. Найти напряженность электрического поля в точке, лежащей посередине между точечными зарядами q 1= -8 нКл и q 2= 4 нКл. Расстояние между зарядами r = 10 см.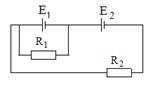
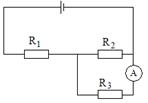 9. Напряжение на зажимах элемента в замкнутой цепи U=2,1 В, сопротивления R1= 5 Ом, R2= 6 Ом, R3= 3 Ом. Какой ток показывает амперметр?
9. Напряжение на зажимах элемента в замкнутой цепи U=2,1 В, сопротивления R1= 5 Ом, R2= 6 Ом, R3= 3 Ом. Какой ток показывает амперметр?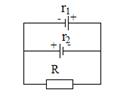 10.
10.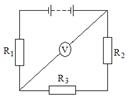 11. ЭДС батареи e=100 В, сопротивления R1= 100 Ом, R2= 200 Ом,
11. ЭДС батареи e=100 В, сопротивления R1= 100 Ом, R2= 200 Ом,


