
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мгновенного центра скоростейСодержание книги
Поиск на нашем сайте
Случай 1
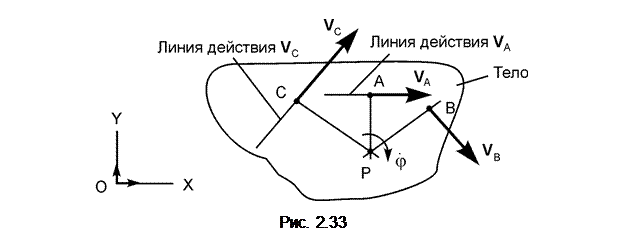
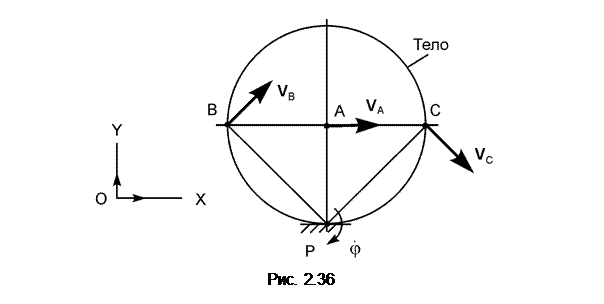
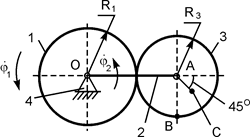
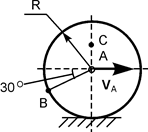
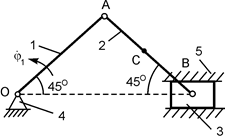
Восстановив перпендикуляры к скоростям в точках А и В, определим положение МЦС (точка Р) и направление вращения тела. Тогда: VA = ω·АР; ω = VA/АР; VВ = ω·ВР; VС = ω·СР; V A ┴ АР; V В ┴ ВР; V С ┴ СР, где ω – модуль угловой скорости В такой последовательности можно определить скорость любой точки тела. На рис. 2.34 – 2.36 представлены другие случаи графического определения МЦС. Порядок определения МЦС для случаев 2, 3, 4 не требует особых комментариев. Все формулы, полученные для первого случая, остаются справедливыми и для остальных случаев.
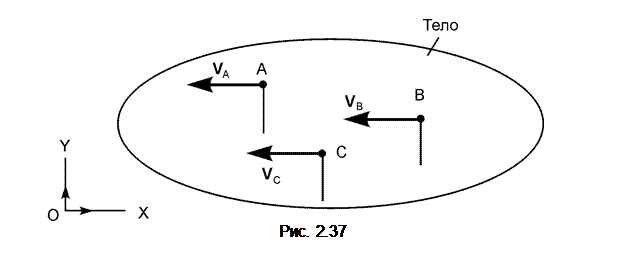
Если скорости точек А и В параллельны, то мгновенный центр скоростей находится в бесконечности (АР = Следует отметить, что при поступательном движении плоской фигуры скорости всех её точек в каждый момент времени также геометрически равны и мгновенный центр скоростей этой фигуры находится в бесконечности. Если условие V A = V B = V C = …остается справедливым в течение некоторого промежутка времени, а не только в отдельный момент, то движение плоской фигуры является поступательным. Если же V A = V B = V C только в некоторый момент времени, то утверждать, что плоская фигура движется поступательно, нельзя. В этом случае говорят, что движение тела является мгновенно поступательным. При мгновенно поступательном движении происходит смена направлений вращения, при этом угло
График зависимости 2.21. Варианты курсового задания К 3 «Кинематический анализ плоского механизма»
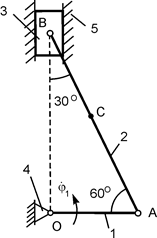
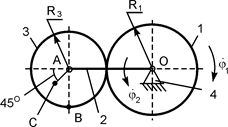
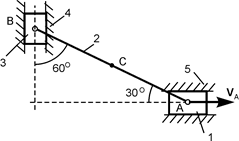
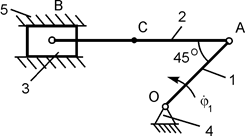
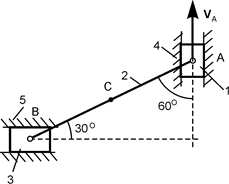
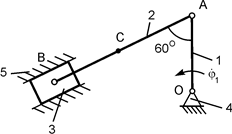
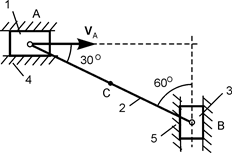
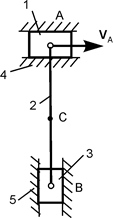
Для закрепления теоретического материала необходимо выполнить курсовое задание К 3. В курсовом задании для расчётного положения плоского механизма требуется найти модули скоростей точек А, В и С и модули угловых скоростей звеньев этого механизма. Схемы механизмов и необходимые для расчёта данные приведены в табл. 2.3.
Таблица 2.3
Продолжение табл. 2.3
Продолжение табл. 2.3
Продолжение табл. 2.3
Продолжение табл. 2.3
Продолжение табл. 2.3
Продолжение табл. 2.3
Окончание табл. 2.3
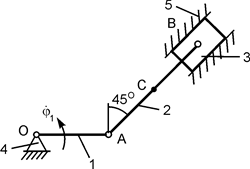
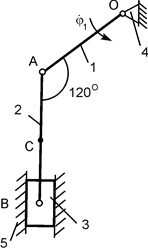
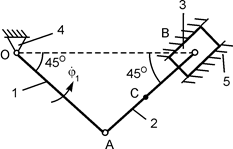
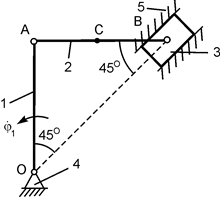
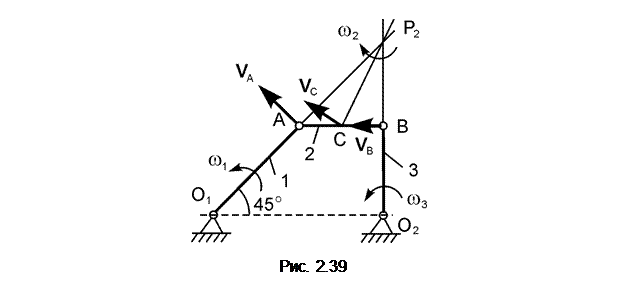
2.22. Пример выполнения курсового задания К 3 Дано: схема плоского механизма (рис. 2.39); модуль угловой скорости ведущего звена 1; ω1 = ωАО1 = 1 рад/с; геометрические параметры: АВ = О2В = 1 м; АС = СВ = 0,5 м. Определить модули скоростей точек А, В, С и модули ω2, ω3 угловых скоростей звеньев АВ и ВО2 механизма. Решение. Согласно расчётной схеме рассматриваемый механизм состоит из трёх звеньев, обозначенных на рис. 2.39 позициями 1, 2, 3. Звено 1 (АО1) ведущее, остальные ведомые. Звенья совершают следующие виды движений: 1 – вращательное, 2 – плоскопараллельное, 3 – вращательное.
Из условия принадлежности точки А звену 1, совершающему вращательное движение, определим модуль скорости V A. VA = ωOA·AO1 = = ω1·AO1 = ω1·(BO2/sin(45о)) = 1·(1/0,707) = 1,414 м/с.
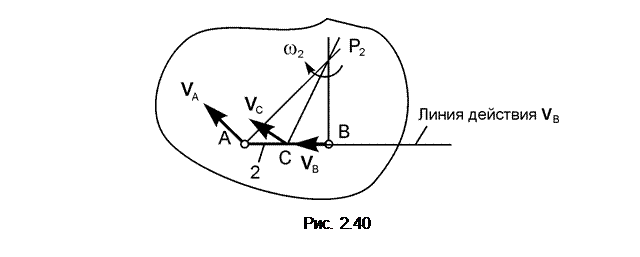
Вектор скорости V A покажем на рис. 2.40. V A ┴ AO1. Как известно, условием безаварийной работы механизма является общая скорость в месте контакта звеньев. Исходя из этого, у звена 2 скорость точки А известна. Точка В, из условия её принадлежности звену 3, описывает окружность, поэтому линия действия скорости V B перпендикулярна ВО2 (V B ┴ BO2). Таким образом, у звена 2 известен вектор V A скорости точки А и линия действия вектора V B. Так как звено 2 совершает плоскопараллельное движение, то для определения мгновенного центра скоростей (точка Р2) используется первый случай (см. рис. 2.33). МЦС находится на пересечении перпендикуляров к скоростям точек А и В. По направлению скорости V A точки А определим направление вращения звена 2 относительно оси, проходящей через точку Р2. Из условия принадлежности точки А звену 2, совершающему плоскопараллельное движение, справедливо равенство VA = ω2·AP2 где ω2 – модуль угловой скорости тела 2. Так как AP2 = AO1 = BO2/sin(45о), то VA = ω2·(BO2/sin(45о)). Из последнего равенства определим модуль ω2 угловой скорости звена 2. ω2 = VA·sin(45о)/BO2 = (1,414·0,707)/1 = 1,000 рад/с. По известному модулю угловой скорости тела 2 определим модули скоростей точек В и С: VB = ω2·BP2 = 1·1 = 1, 000 м/с; VC = ω2·CP2 = ω2· Из условия принадлежности точки В телу 3, совершающему вращательное движение, справедливо равенство VB = ω3·BO2, где ω3 – модуль угловой скорости тела 3. Из этого равенства модуль угловой скорости вращательного движения звена 3 равен ω3 = VB/BO2 = 1/1 = 1,000 рад/с. Полученные результаты расчёта вносятся в таблицу. Таблица
Скорости точек А, В, С показаны на рис. 2.39.
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «поступательное движение твёрдого тела». 2. Записать уравнения поступательного движения тела в пространстве в декартовой системе отсчёта. 3. Записать уравнения поступательного движения тела на плоскости OXY. 4. Записать уравнения прямолинейного поступательного движения тела по горизонтали. 5. Записать выражения для определения проекций скорости центра масс на координатные оси декартовой системы отсчёта. 6. Записать выражение для определения модуля скорости центра масс тела при его поступательном движении в декартовой системе отсчёта. 7. Записать выражения для определения проекций ускорения центра масс на координатные оси декартовой системы отсчёта. 8. Записать выражение для определения модуля ускорения центра масс тела при его поступательном движении в декартовой системе отсчёта. 9. Сформулировать определение термина «вращательное движение твёрдого тела». 10. Записать уравнение вращательного движения тела. 11. Сформулировать определение термина «угловая скорость». 12. Записать формулу для определения угловой скорости вращательного движения тела. 13. Сформулировать определение термина «угловое ускорение». 14. Записать формулу для определения углового ускорения тела. 15. Записать формулу для определения модуля скорости точки при вращательном движении тела. 16. Записать формулу для определения вектора ускорения точки при вращательном движении тела. 17. Записать формулу для определения модуля центростремительного ускорения точки. 18. Записать формулу для определения модуля вращательного ускорения точки. 19. Записать формулу для определения модуля ускорения точки тела при его вращательном движении. 20. Записать уравнение равномерного вращательного движения тела. 21. Записать уравнение равнопеременного вращательного движения тела. 22. При каком сочетании угловой скорости и углового ускорения происходит ускоренное вращение тела? 24. При каком сочетании угловой скорости и углового ускорения происходит замедленное вращение тела? 25. Где прикладывают и как направляют вектор угловой скорости тела? 26. Где прикладывают и как направляют вектор углового ускорения тела при его ускоренном вращении? 27. Сформулировать определение термина «плоскопараллельное движение твёрдого тела». 28. Записать уравнения плоскопараллельного движения тела. 29. Записать формулу для определения вектора скорости точки при плоскопараллельном движении тела. 30. Сформулировать определение термина «мгновенный центр скоростей».
Сложное движение точки
В ряде случаев при решении задач механики оказывается целесообразным (а иногда и необходимым) рассматривать движение точки (или тела) одновременно в двух системах отсчёта, из которых одна остается условно неподвижной, а другая определённым образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называется сложным. Например, шар, катящийся по палубе движущегося парохода, можно считать совершающим по отношению к берегу сложное движение, состоящее из качения по отношению к палубе, с которой связана подвижная система отсчёта OXYZ, и движения вместе с палубой по отношению к берегу, с которым связана неподвижная система отсчёта O1X1Y1Z1. Таким путем сложное движение шара разлагается на два более простых и более легко исследуемых. Возможность разложения сложного движения точки на более простые путём введения дополнительной (подвижной) системы отсчёта широко используется в кинематических и динамических расчётах. Введем следующие понятия, применяемые в сложном движении точки. Движение точки по отношению к неподвижной системе отсчёта O1X1Y1Z1 называется абсолютным и характеризуется абсолютной скоростью V и абсолютным ускорением а (рис. 2.41). Положение точки на траектории абсолютного движения определяется тремя зависящими от времени координатами, которые называются уравнениями абсолютного движения:
X1 = f1(t); Y1 = f2(t); Z1 = f3(t).
cos(V, i) а = cos(а, i 1) = Движение точки по отношению к подвижной системе отсчёта OXYZ называется относительным движением и характеризуется относительной скоростью Vr и относительным ускорением ar (рис. 2.42). Положение точки на траектории относительного движения определяется тремя зависящими от времени координатами, которые называют уравнениями относительного движения: X = f4(t); Y = f5(t); Z = f6(t).
cos(V r, i) cos(V r, k) a r = cos(a r, i) = cos(a r, k) = Пусть координаты точки в подвижной системе отсчёта OXYZ постоянны: X = C1 = const; Y = C2 = const; Z = C3 = const. При этом условии точка неподвижна относительно ПСО, которая совершает движение относительно НСО. Движение этой точки вместе с подвижной системой отсчёта OXYZ относительно неподвижной системы отсчёта O1X1Y1Z1 называется переносным движением, которое характеризуется переносной скоростью V e и переносным ускорением a e(рис. 2.43). Положение точки на траектории переносного движения определяется тремя зависящими от времени координатами, которые называют уравнениями переносного движения:
По известным уравнениям переносного движения находится переносная скорость V e и переносное ускорение a e.
cos(V e, i) = cos(V e, j) = cos(V e, k) = a e = cos(a e, i) = cos(a e, j) = cos(a e, k) =
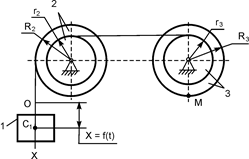
В неподвижной системе отсчёта O1X1Y1Z1 флажок вращается относительно оси O1Y1 с переносной угловой скоростью Траектория относительного движения – прямая линия ОА на флажке. Уравнение относительного движения задано Sr = f(t). Для определения траектории переносного движения поступают следующим образом. Задают время t1 и определяют положение точки М на траектории относительного движения. Sr(t1) = const. Зафиксированная на траектории относительного движения точка М в момент времени t1 вместе с флажком описывает в неподвижной системе отсчёта O1X1Y1Z1 окружность радиусом МК. Эта окружность является траекторией переносного вращения. Необходимо отметить, что в другой момент времени t2 координата точки М на траектории относительного движения Sr(t2) будут иметь другое значение и, следовательно, траекторией переносного движения будет окружность с другим радиусом. Если в каждый момент времени складывать относительное и переносное движения, то получим абсолютное движение. В рассматриваемом примере траекторией абсолютного движения является винтовая линия, сформированная на конусе, образованном прямой ОА на флажке при её вращении относительно оси O1Y1.
Сложение скоростей
Поскольку абсолютное движение представляет собой сумму относительного и переносного движений, то справедлива следующая теорема: при сложном движении абсолютная скорость V точки равна геометрической сумме относительной Vr и переносной Ve скоростей: V = V r + V e. Построенная на рис. 2.45 фигура называется параллелограммом скоростей. Модуль абсолютной скорости находится по формуле
2.25. Сложение ускорений (теорема Кориолиса)
Теорема. При сложном движении точки её абсолютное ускорение равно геометрической сумме относительного, переносного и кориолисова ускорений: a = a r+ a e+ a c, где a r– относительное ускорение; a e – переносное ускорение; a c – ускорение Кориолиса. Доказательство теоремы Кориолиса достаточно сложно и здесь не приводится. Кориолисовым ускорением называется составляющая абсолютного ускорения точки в сложном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки: a c = 2( где Согласно правилу векторного произведения a c ┴
Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки вследствие её относительного движения;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.013 с.) |

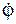 тела.
тела.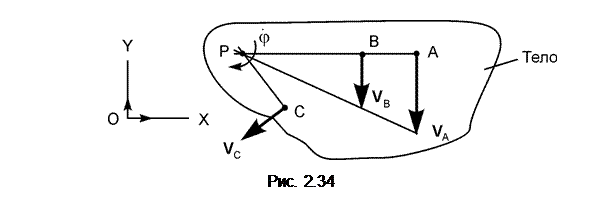
 ; ВР =
; ВР = 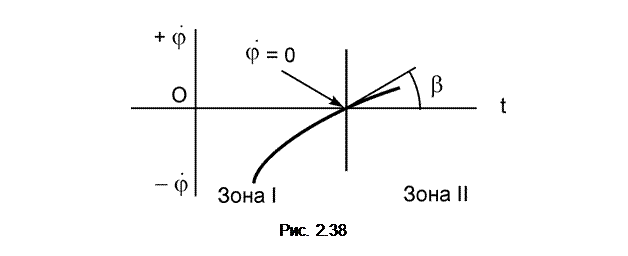
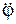 ≠ 0 (рис. 2.38).
≠ 0 (рис. 2.38).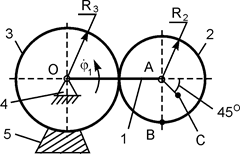
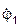 = 1 рад/с;
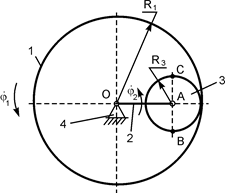
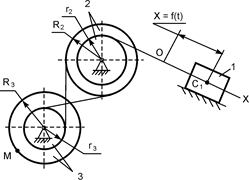
R2 = 0,4 м;
R3 = 0,6 м;
АС = 0,2 м
= 1 рад/с;
R2 = 0,4 м;
R3 = 0,6 м;
АС = 0,2 м
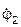 =?
=?
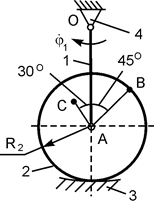
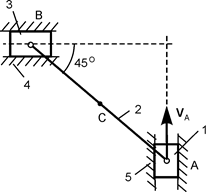
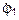 = 1 рад/с;
ОА = 0,60 м;
R2 = 0,24 м;
АС = 0,12 м
= 1 рад/с;
ОА = 0,60 м;
R2 = 0,24 м;
АС = 0,12 м
 =?
=?

 =?
=?






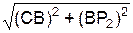 = 1·
= 1· 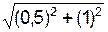 = 1, 118 м/с.
= 1, 118 м/с.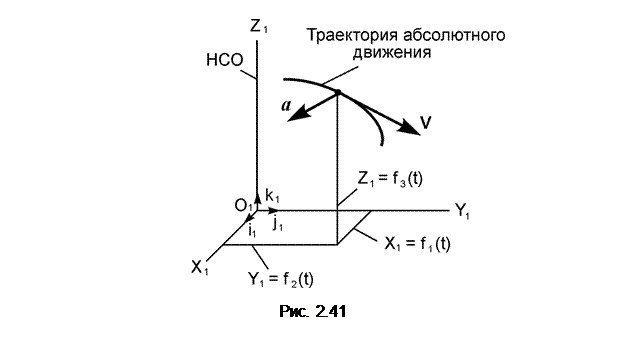
 ;
;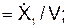 cos(V, j)
cos(V, j) 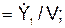 cos(V, k)
cos(V, k) 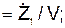
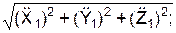
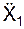 / а; cos(а, j 1) =
/ а; cos(а, j 1) = 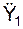 / а; cos(а, k 1) =
/ а; cos(а, k 1) =  / а.
/ а.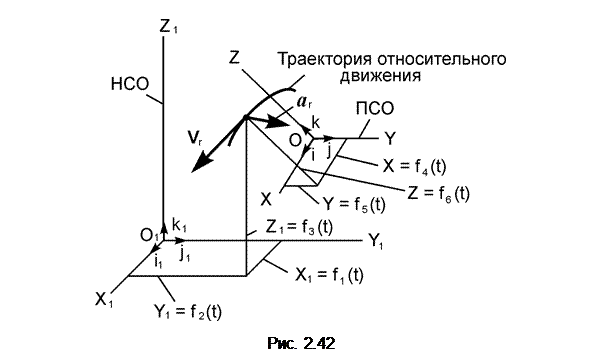

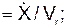 cos(V r, j)
cos(V r, j) 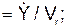
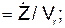
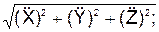
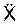 / a r; cos(a r, j) =
/ a r; cos(a r, j) = 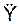 / a r;
/ a r;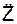 / a r.
/ a r.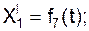
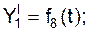
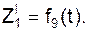

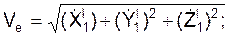
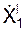 / Ve;
/ Ve;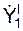 / Ve;
/ Ve;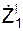 / Ve;
/ Ve;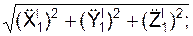
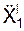 / a e;
/ a e;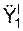 / a e;
/ a e;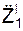 / a e.
/ a e.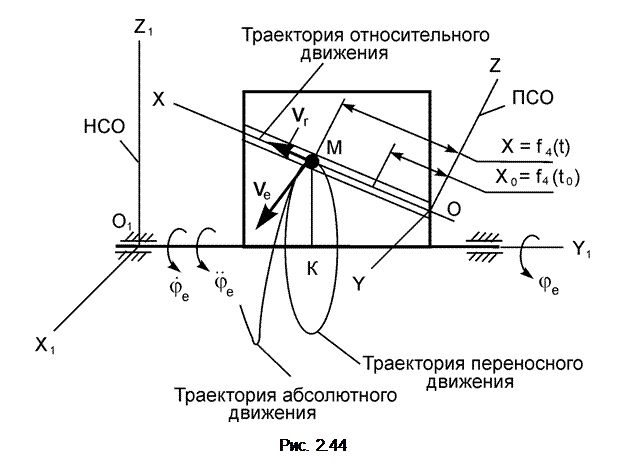
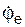 . На флажке закреплена подвижная система отсчёта OXYZ, которая вращается с флажком относительно оси O1Y1. На флажке выполнен канал, по которому движется точка М с относительной скоростью V r.
. На флажке закреплена подвижная система отсчёта OXYZ, которая вращается с флажком относительно оси O1Y1. На флажке выполнен канал, по которому движется точка М с относительной скоростью V r.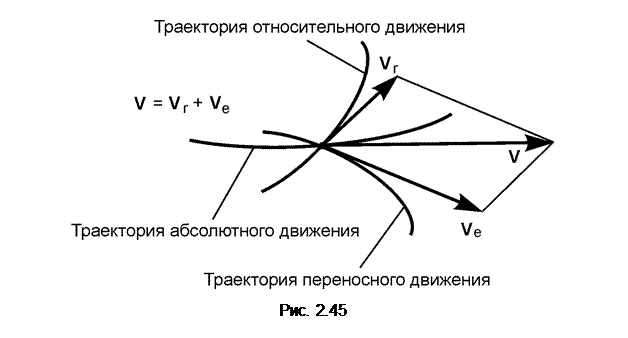
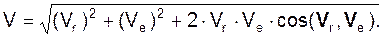
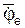 x V r),
x V r),


