Другие типы связей на плоскости

 

 

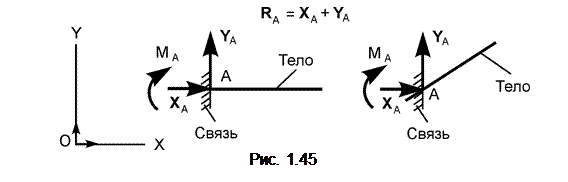
На рис. 1.45 изображена жёсткая заделка (защемление), которая не позволяет механической системе (телу) осуществлять какие-либо движения в плоскости OXY. Поэтому в такой связи реакция R _A раскладывается на компоненты X _A, Y _A по координатным осям и показывается пара сил с алгебраическим моментом М_А.

Таким образом, реакция жёсткой заделки состоит из двух сил X _A, Y _A, расположенных параллельно координатным осям, и реактивного момента М_А. Для определения величины реакции R _A используют формулу

.

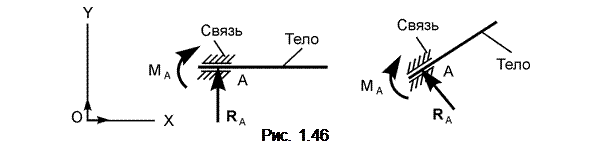
В скользящей заделке (рис. 1.46) показывают реакцию R _A и пару сил с реактивным моментом М_А.

Такая связь позволяет телу перемещаться поступательно вдоль координатной оси ОХ.

В свободной заделке, представляющей собой совокупность скользящей заделки и промежуточной связи, (рис. 1.47) возникает пара сил с моментом М_А, так как допускаются поступательные перемещения тела параллельно составляющим этой связи.

 

Существуют и другие комбинированные связи. Одна из таких связей приведена на рис. 1.48.

Здесь реакция R _A направлена вдоль тела, так как связь допускает незначительные перемещения тела вдоль скользящей заделки. Эта связь не допускает поступательного движения тела на связь и поворот тела в плоскости OXY.

 

1.18. Варианты курсового задания С 1

«Определение реакций опор твёрдого тела»

 

 

Для закрепления теоретического материала необходимо выполнить курсовое задание С 1.

В курсовом задании (см. табл. 1.1) приведены варианты плоских балок, загруженных активными нагрузками Р, М, q, где Р – сосредоточенная сила; М – алгебраический момент пары сил; q – интенсивность распределённой нагрузки.

Используя основную форму уравнений равновесия для плоской произвольной системы сил, определить реакции внешних связей, наложенных на балку. Применяя другую форму уравнений равновесия, проверить правильность расчётов.

 

Таблица 1.1

 

Номер варианта	Расчётная схема	Исходные данные	Определяемые величины
		Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м	ZA =? YA =? RB =?
		Р1 = 20 кН; Р2 = 20 кН; М = 5 кН·м; q = 4 кН/м	ZB =? YB =? RA =?
		Р1 = 10 кН; Р2 = 20 кН; М = 4 кН·м; q = 1 кН/м	ZA =? YA =? RB =?
		Р = 10 кН; М = 6 кН·м; q = 2 кН/м	ZB =? YB =? RA =?

Продолжение табл. 1.1

 

		Р1 = 20 кН; Р2 = 20 кН; М = 5 кН·м; q = 4 кН/м	ZA =? YA =? MA =?
		Р1 = 2 кН; Р2 = 20 кН; М = 4 кН·м; q = 2 кН/м	ZА =? YА =? MA =?
		Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м	ZA =? YA =? МА =?
		Р1 = 4 кН; Р2 = 20 кН; М = 10 кН·м; q = 3 кН/м	ZA =? YA =? RB =?

Продолжение табл. 1.1

 

		Р1 = 10 кН; Р2 = 20 кН; М = 5 кН·м; q = 2 кН/м	ZA =? YA =? RB =?
		Р1 = 15 кН; Р2 = 20 кН; М = 4 кН·м; q = 3 кН/м	ZA =? YA =? RB =?
		Р1 = 10 кН; Р2 = 20 кН; М = 5 кН·м; q = 2 кН/м	ZA =? YA =? МА =?
		Р1 = 12 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м	ZA =? YA =? МА =?

Продолжение табл. 1.1

 

		Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м	ZA =? YA =? RB =?
		Р1 = 20 кН; Р2 = 20 кН; М = 12 кН·м; q = 2 кН/м	ZA =? YA =? RB =?
		Р1 = 20 кН; Р2 = 20 кН; М = 4 кН·м; q = 3 кН/м	ZA =? YA =? МА =?
		Р1 = 14кН; Р2 = 20 кН; М = 4 кН·м; q = 3 кН/м	ZA =? YA =? МА =?

Продолжение табл. 1.1

 

		Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 4 кН/м	ZA =? YA =? RB =?
		Р1 = 20 кН; Р2 = 20 кН; М = 10 кН·м; q = 2 кН/м	ZA =? YA =? RB =?
		Р1 = 10 кН; Р2 = 20 кН; М = 4 кН·м; q = 2 кН/м	ZВ =? YВ =? RА =?
		Р1 = 6 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м	ZA =? YA =? MA =?

Продолжение табл. 1.1

 

		Р1 = 4 кН; Р2 = 20 кН; М = 2 кН·м; q = 1 кН/м	ZA =? YA =? RB =?
		Р1 = 20 кН; Р2 = 20 кН; М = 5 кН·м; q = 2 кН/м	ZA =? YA =? МА =?
		Р1 = 5 кН; Р2 = 10 кН; М = 2 кН·м; q = 3 кН/м	ZA =? YA =? МА =?
		Р1 = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м	ZA =? YA =? MA =?

Продолжение табл. 1.1

 

		Р1 = 6 кН; Р2 = 20 кН; М = 8 кН·м; q = 2 кН/м	ZA =? YA =? MA =?
		Р1 = 20 кН; Р2 = 20 кН; М = 10 кН·м; q = 2 кН/м	ZA =? YA =? MA =?
		Р1 = 10 кН; Р2 = 20 кН; М = 10 кН·м; q = 3 кН/м	ZB =? YB =? RA =?
		Р1 = 15 кН; Р2 = 20 кН; М = 8 кН·м; q = 1 кН/м	ZA =? YA =? МА =?

Окончание табл. 1.1

 

		Р = 5 кН; Р2 = 20 кН; М = 2 кН·м; q = 1 кН/м	ZA =? YA =? MА =?
		Р = 10 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м	ZA=? YA =? MА =?

 

 

Следует ещё раз отметить, что номер варианта задания в контрольной работе студент выбирает самостоятельно, используя методику, приведённую в общих положениях данного пособия.

Цели контрольной работы С 1:

1. Научить студента составлять и решать уравнения равновесия для плоской произвольной системы сил, приложенных к одному телу.

2. Научить студента проводить проверку правильности проведённых результатов расчётов.

 

 

1.19. Пример выполнения курсового задания С 1

 

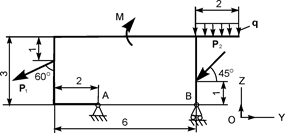
На рис. 1.49 изображена расчётная схема балки.

Дано: P = 20 кН; M = 10 кН·м; q = 2 кНм. Определить реакции внешних связей в точках А и В.

Решение.

Определение реакций внешних связей для рассматриваемой балки проводится согласно алгоритму решения задач статики, приведённому в подразделе 1.7.

1. Выбирается система отсчёта. Так как балка плоская, то выбирается система отсчёта OXY.

2. Выделяется тело, равновесие которого рассматривается. В нашем случае таким телом является балка, изображённая на рис. 1.49.

3. К балке прикладываются активные нагрузки. По условию задачи активные нагрузки известны. Так как задана распределённая нагрузка с интенсивностью q, то её приводят к сосредоточенной силе Q, модуль которой определяют по формуле Q = q×L = 2×2 = 4 кН. Эту сосредоточенную силу прикладывают к телу и показывают размер, на котором она приложена. Таким образом, на балку действуют следующие активные нагрузки: P, Q – активные силы; активная пара сил с алгебраическим моментом М.

4. Согласно аксиоме связей внешние связи, наложенные на механическую систему в точках А и В, отбрасывают и показывают реакции внешних связей X _A, Y _A, R _B. Таким образом, на балку действуют внешние нагрузки, состоящие из активных нагрузок: P, Q, M и реакций внешних связей: X _A, Y _A, R _B.

5. Так как система внешних сил, действующих на тело, является плоской и произвольной, то записывают три уравнения равновесия:

Σ + Σ = 0 = Q – P·cos(60^о) + X_A = 0; (1)

Σ + Σ = 0 = – P·sin(60^о) + R_B + Y_A = 0; (2)

Σ M_A(F _i^E) + Σ M_A(R _i^E) = 0 =

= M + P·sin(60⁰)×2 – P·cos(60^о)·1 – R_B×4 = 0. (3)

При составлении выражений (1), (2), (3) использована первая форма уравнений равновесия. Эти уравнения решают в наиболее удобной последовательности и находят проекции неизвестных реакций на координатные оси системы отсчёта OXY или модули этих реакций.

Из уравнения (1) X_A= – Q + P·cos(60^о) = – 4 + 20×0,5 = 6,000 кН.

Из уравнения (3) R_B = (M + P·sin(60^о)×2 – P·cos(60^о)×1)4 =

= (10 + 20×0,866×2 – 20×0,5×1)4 = 8,660 кН.

Из уравнения (2)

Y_A= – R_B + P·sin(60^о) = – 8,66 +20×0,866 = 8,660 кН.

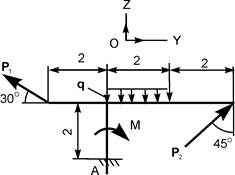
Согласно условию задания необходимо произвести проверку правильности проведённых расчётов. С целью такой проверки изобразим рассматриваемую балку в упрощённом варианте (рис. 1.50).

Сила Р разложена на составляющие силы по координатным осям. Это упрощает проецирование силы Р на координатные оси системы отсчёта OXY. Необходимо отметить, что силы раскладываются на составляющие по координатным осям системы отсчёта только в точке их приложения. Порядок решения задачи остается прежним, только использована третья форма уравнений равновесия.

 

Σ M_С(F _i^E) + Σ M_С(R _i^E) = 0 =

= M – Q·1 – R_B·2 + Y_A·2 – X_A·1 = 0; (4)

Σ M_D(F _i^E) + Σ M_D(R _i^E) = 0 =

= M – Q·1 + P·sin(60^о)·2 – R_B·4 – X_A·1 = 0; (5)

Σ M_Е(F _i^E) + Σ M_Е(R _i^E) = 0 =

= M – P·sin(60⁰)·2 – P·cos(60^о)·1 + Y_A·4 = 0. (6)

Подставляя найденные значения реакций X _A, Y _A, R _B в выражения (4), (5), (6) и вычислив, получим:

 

Σ M_С(F _i^E) + Σ M_С(R _i^E) = 0 =

= 10 – 4·1 – 8,660·2 + 8,660·2 – 6·1 = 0; (4^I)

Σ M_D(F _i^E) + Σ M_D(R _i^E) = 0 =

= 10 – 4·1 + 20·0,866·2 – 8,660·4 – 6·1 = 0; (5^I)

Σ M_Е(F _i^E) + Σ M_Е(R _i^E) = 0 =

= 10 – 20·0,866·2 – 20·0,5·1 + 8,660·4 = 0. (6^I)

 

Проведённая проверка подтвердила правильность результатов расчётов. Результаты вычислений помещают в таблицу.

Таблица

 

Реакции и их размерность	XA,кН	YA,кН	RB,кН
Численные значения реакций	6,000	8,660	8,660

Общие рекомендации по выполнению курсового задания

1.На каждом чертеже должны быть размеры. Чертежи выполняются в масштабе.

2.Силы следует раскладывать в точках их приложения на составляющие по координатным осям системы отсчёта.

3.Выбирается та форма уравнений равновесия, которая обеспечивает минимум вычислительных работ. В уравнении моментов рекомендуется находить точки, где пересекается наибольшее число линий действия сил.

4.Производится проверка правильности результатов расчётов.

 

 

Вопросы и задания для самоконтроля

 

 

1. Сформулировать определение понятия «плоская произвольная система сил».

2. Сформулировать теорему, выражающую метод Пуансо для произвольной системы сил.

3. Записать геометрическое условие равновесия произвольной системы сил.

4. Записать первую форму уравнений равновесия плоской произвольной системы сил.

5. Записать вторую форму уравнений равновесия плоской произвольной системы сил.

6. Записать третью форму уравнений равновесия плоской произвольной системы сил.

7. Записать векторную формулу для определения главного вектора сил.

8. Записать формулу для определения модуля главного вектора сил в декартовой системе отсчёта.

9. Записать векторную формулу для определения главного момента системы сил относительно центра приведения.

 

 

Расчёт фермы

 

 

Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция. При этом все стержни фермы прямолинейные. Если оси всех стержней фермы лежат в одной плоскости, то её называют плоской фермой. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основания, называют опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру – нижний пояс фермы. Вертикальные стержни называют стойками, а наклонные раскосами.

На рис. 1.51 изображена плоская ферма, состоящая из 17 стержней.

Совокупность стержней 2, 6, 10, 14 образует верхний пояс фермы, а совокупность стержней 4, 8, 12, 16 образует нижний пояс фермы.

В теоретической механике рассматривают идеализированные фермы, при расчёте которых приняты следующие допущения:

1. Все внешние нагрузки к ферме прикладываются только в узлах.

2. Все шарниры считаются идеальными, т. е. трение в узлах фермы не учитывается.

3. Все стержни невесомые, т. е. они загружены только по концам.

4. Все силы, действующие на ферму, лежат в одной плоскости.

На каждый из стержней фермы действуют две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или сжатие.

В реальных фермах может и не быть шарниров, а при жёстком соединении сваркой или заклёпками стержни могут воспринимать и другие виды нагрузок (изгиб, кручение и т. д.). Однако результаты вычислений при принятых допущениях вполне пригодны для практики, причем расчёт усилий в стержнях существенно облегчается.

 

 

Методология расчёта усилий

В стержнях плоской фермы

Методологию расчёта усилий в стержнях плоской фермы покажем на примере выполнения курсового задания С 2, которое входит в контрольную работу обучающегося.

 

 

1.21.1. Варианты курсового задания С 2

«Определение реакций опор и сил

в стержнях плоской фермы»

 

 

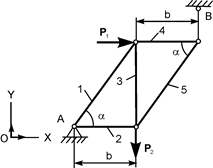
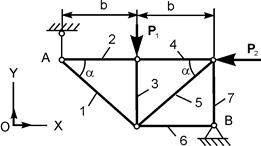
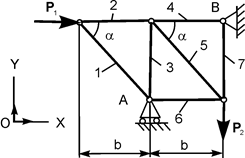
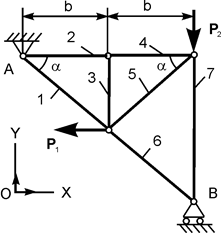
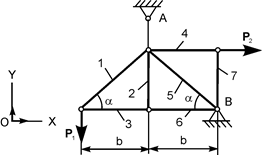
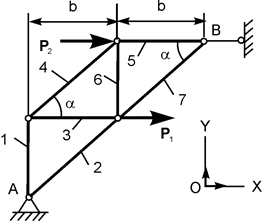
В курсовом задании С 2 требуется определить реакции опор фермы в зависимости от заданных сил Р ₁, Р ₂, а также усилия S _i в стержнях. Варианты расчётных схем и нагрузки, действующие на фермы, приведены в табл. 1.2.

Таблица 1.2

 

Номер варианта	Расчётная схема	Исходные данные	Определяемые величины	Реакции, определяемые по методу Риттера
		P1 = 4 кН; Р2 = 9 кН; a = 30^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6
		P1 = 2 кН; Р2= 12 кН; a = 60^о; b = 2 м	XВ; YВ; RА; S1 – S6	S1; S4; S6
		P1 = 10 кН; Р2 = 10 кН; a = 60^0; b = 2 м	XA; YA; RB; S1 – S5	S2; S3; S4
		P1 = 2 кН; Р2 = 12 кН; a = 45^0; b = 2 м	XA; YA; RB; S1 – S8	S3; S4; S5

Продолжение табл. 1.2

 

		P1 =2 кН; Р2 =4 кН; a = 60^0; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6
		P1 =3 кН; Р2 =7 кН; a = 45^0; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S7
		P1 =4 кН; Р2 =6 кН; a = 60^0; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6
		P1 =5 кН; Р2 =7 кН; a = 45^0; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6

Продолжение табл. 1.2

 

		P1 = 10 кН; Р2 = 8 кН; a = 60^о; b = 2 м	XВ; YВ; RА; S1 – S9	S4; S5; S6
		P1 = 3 кН; Р2 = 4 кН; a = 45^о; b = 2 м	XA; YA; RB; S1 – S7	S1; S5; S6
		P1 = 2 кН; Р2 = 6 кН; a = 45^о; b = 2 м	XA; YA; RB; S1 – S7	S2; S3; S7
		P1 = 5 кН; Р2 = 7 кН; a = 45^о; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6

Продолжение табл. 1.2

 

		P1 = 4 кН; Р2 = 6 кН; a = 45^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6
		P1 = 3 кН; Р2 = 5 кН; a = 30^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6
		P1 = 2 кН; Р2 = 2 кН; a = 60^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6
		P1 = 5 кН; Р2 = 6 кН; a = 60^о; b = 2 м	XA; YA; RB; S1 – S5	S2; S3; S4

Продолжение табл. 1.2

 

		P1 = 4 кН; Р2 = 4 кН; a = 30^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6
		P1 = 5 кН; Р2 = 2 кН; a = 60^о; b = 2 м	XВ; YВ; RА; S1 – S7	S2; S3; S4
		P1 =5 кН; Р2 =7 кН; a = 45^о; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6
		P1 =2 кН; Р2 =3 кН; a = 30^о; b = 2 м	XA; YA; RB; S1 – S5	S2; S3; S4

Продолжение табл. 1.2

 

		P1 = 3 кН; Р2 = 2 кН; a = 45^о; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6
		P1 = 2 кН; Р2 = 4 кН; a = 45^о; b = 2 м	XA; YA; RB; S1 – S9	S2; S7; S8
		P1 = 5 кН; Р2 = 8 кН; a = 30^о; b = 2 м	XA; YA; RB; S1 – S7	S2; S3; S4
		P1 = 6 кН; Р2 = 10 кН; a = 45^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6

Продолжение табл. 1.2

 

		P1 = 7 кН; Р2 = 10 кН; a = 45^о; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6
		P1 = 8 кН; Р2 = 12 кН; a = 30^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6
		P1 = 9 кН; Р2 = 14 кН; a = 45^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S6; S7
		P1 = 10 кН; Р2 = 5кН; a = 30^о; b = 2 м	XA; YA; RB; S1 – S7	S2; S3; S4

Продолжение табл. 1.2

 

		P1 = 12 кН; Р2 = 8 кН; a = 45^о; b = 2 м	XВ; YВ; RА; S1 – S7	S4; S5; S6
		P1 = 5 кН; Р2 = 10 кН; a = 45^о; b = 2 м	XA; YA; RB; S1 – S7	S4; S5; S6