
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По заданным уравнениям её движения»Содержание книги
Поиск на нашем сайте
Для закрепления теоретического материала рекомендуется выполнить курсовое задание К 1. По заданным уравнениям движения точки М (табл. 2.1) установить вид её траектории и для момента времени t1 найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории. Таблица 2.1
Окончание табл. 2.1
2.13. Пример выполнения курсового задания К 1
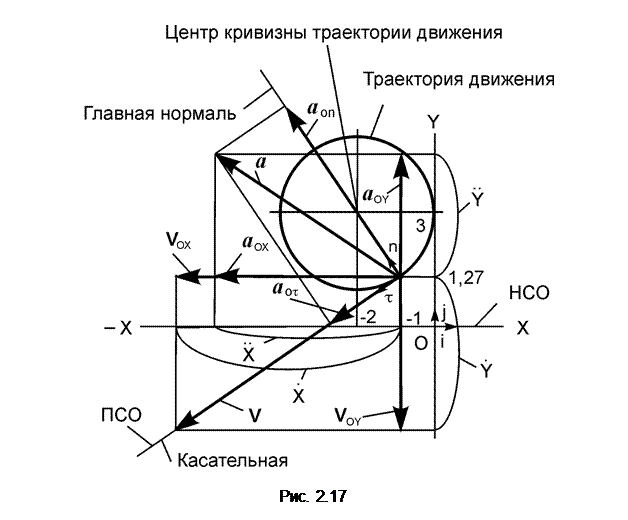
Исходные данные: X = X(t) = 2·cos(p·t2/3) – 2; см. (1) Y = Y(t) = – 2·sin(p·t2/3) + 3; см. (2) t1 = 1 c. По заданным уравнениям движения точки на плоскости определить кинематические характеристики в момент времени t1. Решение. 1. Для определения траектории движения точки уравнения (1) и (2) связываются через параметр t. Уравнения (1) и (2) выразим в следующем виде: X + 2 = 2·cos(p·t2/3); (1I) Y – 3 = – 2·sin(p·t2/3). (2I) Возведём в квадрат левые и правые части уравнений (1I), (2I) и сложим их. (X + 2)2 = (2·cos(p·t2/3))2; (1II) + (Y – 3)2 = (– 2·sin(p·t2/3))2. (2II) После сложения уравнений (1II), (2II) получим (X + 2)2 + (Y – 3)2 = (2·cos(p·t2/3))2 + (– 2·sin(p·t2/3))2 = = 22·((cos(p·t2/3))2 + (sin(p·t2/3)))2 = 22·1 = 22. При преобразованиях использована тригонометрическая формула sin2(α) + cos2(α) = 1. Полученное уравнение (X + 2)2 + (Y– 3)2 = 22 есть уравнение окружности (x – a)2+(y – b)2 = r2 c центром в точке с координатами (a, b). Построим график траектории движения точки (рис. 2.17).
2. Определение положения точки на траектории её движения в момент времени (t1). В уравнения (1) и (2) подставляем время t1. X(t1) = 2·cos(p·(t1)2/3) – 2 = 2·cos(p·(1)2/3) – 2 = = 2·0,5 – 2 = 1,000 см < 0. Y(t1) = – 2·sin(p·(t1)2/3) + 3 = – 2·sin(p·(1)2/3) + 3 = = – 2·0,866 + 3 = 1,270 см > 0. Точку с координатами (–1, 1,270) показываем на траектории её движения. ВНИМАНИЕ! Если точка не попала на траекторию её движения, то: 1) неверно определена траектория движения; 2) неверно подсчитаны значения координат точки. 3. Определение скорости точки. Для определения скорости точки найдем производные по времени от соответствующих уравнений её движения:
Вычислим значения проекций
=(– 4·3,14/3)·sin(p·12/3)·1 = – 3,625 см/с < 0;
=(– 4·3,14/3)·cos(p·12/3)·1 = – 2,093 см/с < 0. Так как На векторах V OX, V OY строим вектор V по правилу параллелограмма. Вектор скорости V направлен по касательной к траектории движения точки. ВНИМАНИЕ! Если вектор V направлен не по касательной к траектории движения, то: 1) неверно взяты производные 2) неверно вычислены значения
Вычисляется модуль V скорости V в момент времени (t1) по формуле
= В ряде вариантов можно определить модуль скорости по формуле
= 4·p·t/3. V(t1) = 4·p·t1/3 = 4·3,14·1/3 = 4,186 см/с. 4. Определение ускорения точки. Находятся производные по времени от проекций Так как проекция
Аналогично
Определим
Так как ВНИМАНИЕ! Если ускорение a направлено не в сторону вогнутости траектории движения, то: 1) неверно взяты производные 2) неверно вычислены значения
Определяется модуль ускорения по формуле a (t1) = 5. Определение касательного и нормального ускорений. На рис. 2.17 наносим подвижную систему отсчёта (ПСО). Разложим полное ускорение a на касательное а oτ и нормальное а on ускорения. Так как касательное ускорение а oτ совпадает с направлением скорости V, то точка движется ускоренно. Модуль а oτ касательного ускорения в момент времени t1 находится по формуле а oτ(t1) = | = |((– 3,625)·(– 8,020) + (– 2,099)·5,510)/4,186| = 4,186 см/с2. Касательное ускорение характеризует быстроту изменения величины скорости, поэтому его проекция на касательную может быть определена по формуле
Так как Модуль нормального ускорения находится по формуле а on(t1) = = Из формулы а on = V2/ρ определяется радиус кривизны траектории движения ρ(t1) = V2(t1)/(а on(t1)) = (4,186)2/8,780 = 2,0 см. Таким образом, радиус кривизны траектории движения равен радиусу окружности, по которому перемещается точка. Результаты вычислений заносятся в таблицу. Таблица
Окончание таблицы
Вопросы и задания для самоконтроля
1. Сформулировать определение термина «кинематика». 2. Сформулировать определение термина «механическое движение». 3. Записать уравнения движения точки в декартовой системе отсчёта (точка движется в пространстве). 4. Записать уравнения движения точки в декартовой системе отсчёта (точка движется в горизонтальной плоскости). 5. Записать уравнения движения точки в декартовой системе отсчёта (точка движется параллельно оси ОХ). 6. Записать уравнение траектории движения точки в декартовой системе отсчёта (точка движется в вертикальной плоскости OYZ). 7. Сформулировать определение термина «скорость». 8. Записать формулу для определения скорости точки через компоненты скорости в декартовой системе отсчёта. 9.Записать формулы для определения проекций скорости на координатные оси в декартовой системе отсчёта. 10. Записать формулу для определения модуля скорости через её проекции в декартовой системе отсчёта. 11. Записать формулы для определения направляющих косинусов при ориентации скорости в декартовой системе отсчёта. 12. Как направлена скорость точки по отношению к траектории её движения? 13. Сформулировать определение термина «ускорение». 14. Куда направлено ускорение точки по отношению к криволинейной траектории её движения? 15. Записать формулу для определения ускорения точки через компоненты ускорения в декартовой системе отсчёта. 16. Записать формулы для определения проекций ускорения на координатные оси в декартовой системе отсчёта. 17. Записать формулу для определения модуля ускорения через его проекции в декартовой системе отсчёта. 18. Записать формулы для определения направляющих косинусов при ориентации ускорения в декартовой системе отсчёта. 19. Записать уравнение равнопеременного прямолинейного движения точки в декартовой системе отсчёта. 20. Записать формулу равномерного прямолинейного движения точки в декартовой системе отсчёта. 21. Записать уравнение движения точки в естественных координатах. 22. Записать формулу для определения вектора скорости точки в естественных координатах. 23. При каком условии точка движется в сторону увеличения дуговой координаты? 24. При каком условии точка движется в сторону уменьшения дуговой координаты? 25. Записать формулу для определения модуля скорости в естественных координатах. 26. Записать формулу для определения вектора ускорения в естественных координатах. 27. Сформулировать определение термина «касательное ускорение». 28. Сформулировать определение термина «нормальное ускорение». 29. Записать формулу для определения вектора касательного ускорения. 30. Записать формулу для определения вектора нормального ускорения. 31. Записать формулу для определения модуля ускорения точки при естественном способе задания движения точки. 32. Записать формулу для определения модуля касательного ускорения с использованием проекций скорости и ускорения на координатные оси декартовой системы отсчёта. 33. Как движется точка, если проекции её скорости и ускорения на касательную совпадают по знакам? 34. Как движется точка, если проекции её скорости и ускорения на касательную не совпадают по знакам? 35. Что характеризует касательное ускорение? 36. Что характеризует нормальное ускорение? 37. Чему равен радиус кривизны траектории при прямолинейном движении точки? 38. При каких условиях происходит прямолинейное движение точки? 39. При каких условиях происходит равномерное криволинейное движение? 40. При каких условиях происходит неравномерное криволинейное движение? 41. Записать уравнение движения точки при векторном способе задания её движения. 42. Записать формулу для определения скорости точки при векторном способе задания её движения. 43. Записать формулу для определения ускорения точки при задании её движения векторным способом. 44. Записать уравнение равнопеременного движения точки в естественных координатах. 45. Записать уравнение равномерного движения точки в естественных координатах.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 867; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.200.121 (0.007 с.) |

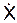 = 2·(– sin(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(sin(p·t2/3))·t;
= 2·(– sin(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(sin(p·t2/3))·t;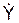 = – 2·(cos(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(cos(p·t2/3))·t.
= – 2·(cos(p·t2/3)·(2·p·t/3)) = (– 4·p/3)·(cos(p·t2/3))·t.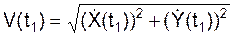 =
=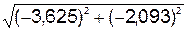 = 4,186 см/с.
= 4,186 см/с.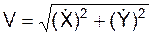 = =
= = 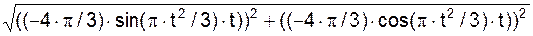 =
=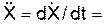 (– 8·p2/9)·cos(p·t2/3)·t2 – (4·p/3)·sin(p·t2/3).
(– 8·p2/9)·cos(p·t2/3)·t2 – (4·p/3)·sin(p·t2/3).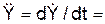 (8·p2/9)·sin(p·t2/3)·t2 – (4·p/3)·cos(p·t2/3).
(8·p2/9)·sin(p·t2/3)·t2 – (4·p/3)·cos(p·t2/3).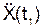 и
и 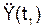 , подставляя в последние формулы значение времени t1. Произведя расчеты, получим:
, подставляя в последние формулы значение времени t1. Произведя расчеты, получим: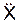 ,
, 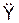 ;
;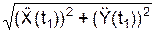 =
= 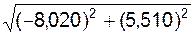 = 9,730 см/с2.
= 9,730 см/с2.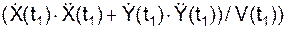 | = |
| = |  (t1)| =
(t1)| =
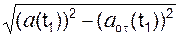 =
=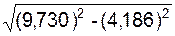 = 8,780 см/с2.
= 8,780 см/с2.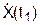 , см/с
, см/с
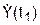 , см/с
, см/с
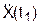 , см/с2
, см/с2
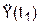 , см/с2
, см/с2



