
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Естественные координатные осиСодержание книги
Поиск на нашем сайте
Точка перемещается в пространстве по заданному уравнению движения S = f(t) (рис. 2.12). Проведём в точке М кривой АВ соприкасающуюся плоскость, нормальную плоскость, перпендикулярную соприкасающейся плоскости, и спрямляющую плоскость, перпендикулярную соприкасающейся и нормальной плоскостям. Пересечением трёх плоскостей образован естественный трёхгранник. Линию пересечения соприкасающейся и нормальной плоскостей называют главной нормалью. Линию пересечения спрямляющей и соприкасающейся плоскостей называют касательной. Линию пересечения спрямляющей и нормальной плоскостей называют бинормалью.
Естественными координатными осями называют три взаимно перпендикулярные оси: касательная (единичный вектор τ всегда направлен в сторону возрастания дуговой координаты S); главная нормаль (единичный вектор n направлен в сторону вогнутости траектории); бинормаль (единичный вектор b перпендикулярен векторам τ и n и направлен так же, как и вектор k по отношению к векторам i, j в правой декартовой системе отсчёта OXYZ) (рис. 2.13).
Если в правой системе отсчёта OXYZ смотреть на единичные векторы I, j с положительного направления оси OZ (навстречу вектору k), то для совпадения направлений векторов i, j вектор i необходимо поворачивать против хода часовой стрелки. По такому же правилу ориентируются в пространстве векторы τ, n, b. Начало естественных координатных осей всегда располагается в точке (см. рис. 2.12) и при движении по траектории перемещается вместе с ней. Естественные координатные оси, оставаясь взаимно перпендикулярными, изменяют своё направление в пространстве. Следовательно, естественные координатные оси образуют подвижную систему отсчёта (ПСО).
На рис. 2.14 орты τ и n расположены в соприкасающейся плоскости, а орт b не виден, так как он перпендикулярен ортам τ и n и плоскости рисунка. Главная нормаль всегда проходит через центр кривизны траектории движения точки. Здесь ρ – радиус кривизны траектории движения. При движении точки по окружности радиусом R радиус кривизны траектории ρ = R. При движении точки по прямой линии ρ =
Скорость точки
Скорость точки при естественном способе задания движения определяется по формуле V = τ ·(dS/dt) = τ · где dS/dt = Символ (·) означает однократное дифференцирование функции S = f(t) по времени. Таким образом, проекция скорости на касательную равна первой производной по времени от уравнения движения S = f(t). В данном учебно-методическом пособии проекцию скорости V на касательную принято обозначать Как известно, вектор V скорости точки всегда направлен по касательной к траектории движения. Проекция скорости на касательную может быть положительной, отрицательной и равной нулю. Если в некоторый момент времени Если Если, непрерывно изменяясь, Модуль скорости V находят по формуле V = |
Ускорение точки
Ускорение а точки всегда направлено в сторону вогнутости траектории движения, лежит в соприкасающейся плоскости (см. рис. 2.14) и находится по формуле a = а oτ + а on, где а oτ – касательное ускорение; а on – нормальное ускорение.
Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной нормали и называется нормальным ускорением, а другой направлен по касательной и называется касательным ускорением.
Касательное а oτ и нормальное а on ускорения называют также компонентами ускорения по естественным координатным осям. Касательное ускорение а oτ характеризует быстроту изменения величины скорости V и находится по формуле а oτ = τ · (d2S/dt2) = τ · ( где Таким образом, проекция ускорения точки на касательную равна второй производной по времени от дуговой координаты S = f(t) или первой производной по времени от проекции скорости на касательную. Символ (··) означает двойное дифференцирование функции S = f(t) по времени. Из приведённых обозначений проекций ускорения на касательную, как правило, используют обозначение Эта проекция ( Касательное ускорение а oτ характеризует быстроту изменения величины скорости. Нормальное ускорение а on характеризует быстроту изменения направления скорости и находится по формуле а on = n ·( Так как При прямолинейном движении точки радиус кривизны траектории движения ρ = Таким образом, нормальное ускорение существует только при криволинейном движении. В случае естественного способа задания движения, когда известна траектория точки, а, следовательно, её радиус кривизны ρ в любой точке и уравнение движения S = f(t), можно найти проекции ускорения точки на естественные координатные оси и по ним определить модуль и направление ускорения по формулам: a = cos(а, i) = Модули скорости и ускорения точки при естественном и координатном способах задания движения точки связаны следующими зависимостями: V = | a = а oτ = |
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |




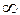 . В остальных случаях при движении точки по криволинейной траектории радиус её кривизны является переменной величиной.
. В остальных случаях при движении точки по криволинейной траектории радиус её кривизны является переменной величиной. ,
, = τ ·
= τ ·  ,
,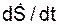 – проекция ускорения a точки на касательную.
– проекция ускорения a точки на касательную. /ρ).
/ρ). ;
; ;
; ;
; |.
|.


