Программа раздела «кинематика»

 

 

Введение в кинематику. Предмет кинематики. Пространство и время в классической механике. Система отсчёта. Задачи кинематики.

Кинематика точки. Координатный способ задания движения точки (в декартовых координатах). Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси.

Естественный способ задания движения точки. Естественные координатные оси. Определение скорости и ускорения точки по их проекциям на оси естественного трёхгранника. Касательное и нормальное ускорения точки. Равномерное и равнопеременное движения точки, законы этих движений.

Векторный способ задания движения точки. Определение скорости и ускорения точки. Пример выполнения курсового задания К 1.

Поступательное движение твёрдого тела. Уравнения движения. Теорема о траекториях, скоростях и ускорениях точек твёрдого тела при поступательном движении.

Вращение твёрдого тела вокруг неподвижной оси (вращательное движение). Уравнение вращательного движения твёрдого тела. Угловая скорость и угловое ускорение твёрдого тела. Законы равномерного и равнопеременного вращений. Скорость и ускорение точки твёрдого тела. Векторы угловой скорости и углового ускорения. Пример выполнения курсового задания К 2.

Плоскопараллельное (плоское) движение твёрдого тела. Уравнения плоскопараллельного движения. Определение скорости точки плоской фигуры как геометрической суммы скорости полюса и скорости этой точки при вращении фигуры относительно оси, проходящей через полюс. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Пример выполнения курсового задания К 3.

Сложное движение точки и твёрдого тела. Абсолютное и относительное движения точки. Переносное движение. Относительные, переносные и абсолютные скорость и ускорение точки. Теорема о сложении скоростей. Теорема Кориолиса о сложении ускорений. Модуль и направление кориолисова ускорения. Случай поступательного переносного движения. Пример выполнения курсового задания К 4.

Сферическое движение твёрдого тела. Уравнения движения тела. Мгновенная угловая скорость тела. Примеры решения задач.

Свободное движение твёрдого тела. Основные понятия и определения. Уравнения движения.

Примечания:

1. По решению кафедры в рабочую программу могут включаться дополнительные вопросы, перечень которых должен быть сообщен студентам.

2. При обучении студентов другим специальностям решением кафедры или деканата из рабочей программы могут быть исключены некоторые вопросы.

 

 

При написании данного учебно-методического пособия использованы следующие литературные источники информации:

1. Тарг С. М. Краткий курс теоретической механики: Учеб. для вузов. – М.: Высш. шк., 2002. – 416 с.: ил.

2. Яблонский А. А., Никифорова В. М. Курс теоретической механики. Ч. I. Статика. Кинематика: Учебник для втузов. – Изд. 5-е, испр. – М.: Высш. школа, 1977. – 368 с. с ил. и последующие издания.

3. Мещерский И. В. Сборник задач по теоретической механике: Учеб. пособие/ Под ред. Н. В. Бутенина, А. И. Лурье, Д. Р. Меркина. – М.: Наука, 1986. – 448 с. и последующие издания.

4. Сборник заданий для курсовых работ по теоретической механике: Учеб. пособие для техн. вузов/ А. А. Яблонский, С. С. Норейко, С. А. Вольфсон и др.; Под ред. А. А. Яблонского. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1985. – 367 с.

5. Горбач Н. И. Теоретическая механика: Динамика: Учеб. пособие. – Мн.: Книжный Дом, 2004. – 192 с. (Экспресс-курс).

6. Тульев В. Д. Теоретическая механика: Статика. Кинематика: Учеб. пособие. – Мн.: Книжный Дом, 2004. – 152 с. (Экспресс-курс).

7. Лукин А. М., Лукин Д. А., В. В. Квалдыков. Теоретическая механика (разделы «Статика», «Кинематика»): Учебно-методическое пособие для студентов заочной и дистанционной форм обучения при подготовке дипломированного специалиста по направлению «СТРОИТЕЛЬСТВО». – Омск: Изд-во СибАДИ, 2007. – 287 с.

8. Лукин А. М., В. В. Квалдыков. Теоретическая механика (раздел «Динамика»): Учебно-методическое пособие для студентов заочной и дистанционной форм обучения при подготовке дипломированного специалиста по направлению «СТРОИТЕЛЬСТВО». – Омск: Изд-во СибАДИ, 2008. – 372 с.

10. Теоретическая механика. Терминология. Буквенные обозначения величин: Сборник рекомендуемых терминов. – М.: Наука, 1988. – Вып. 102. – 88 с.

 

 

РАЗДЕЛ ПЕРВЫЙ

 

СТАТИКА

 

 

Основные понятия статики

 

 

В основу каждого раздела механики положен ряд понятий и определений, принята система аксиом, т. е. важнейших положений, многократно подтверждённых практикой. Приступая к изучению статики, следует определить основные понятия, встречающиеся в этом разделе механики.

 

Статика – раздел механики, в котором изучают условия равновесия механических систем под действием сил.

 

Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства.

 

Масса является мерой инертности точки и мерой инертности тела при его поступательном движении. Масса измеряется в кг.

 

Инертность – свойство материального тела, проявляющееся в сохранении движения, совершаемого им при отсутствии действующих сил, и в постепенном изменении этого движения с течением времени, когда на тело начинают действовать силы.

Материальная точка – точка, имеющая массу.

 

Материальная точка не имеет размеров и обладает способностью взаимодействовать с другими материальными точками.

 

Абсолютно твёрдое тело – материальное тело, в котором расстояние между двумя любыми точками остается неизменным (рис. 1.1).

 

 

В природе такие тела отсутствуют, так как каждое тело деформируется в результате приложенных воздействий. Однако принятое допущение (абсолютно твёрдое тело) значительно упрощает изучение действия сил на тело и условий, при которых эти силы уравновешиваются. В дальнейшем абсолютно твёрдые тела условлено называть телами.

 

Механическая система – любая совокупность материальных точек.

 

Движения материальных точек в механической системе взаимозависимы. В механике тело рассматривают как механическую систему, образованную непрерывной совокупностью материальных точек. Тела могут взаимодействовать друг с другом.

 

Механическое действие – действие на данное тело со стороны других тел, которое приводит к изменению скоростей точек этого тела или следствием которого является изменение взаимного положения точек данного тела.

 

Другими словами, при механическом действии тело приобретает механическое движение.

 

Механическое движение – изменение с течением времени взаимного положения тел в пространстве или взаимного положения частей данного тела.

Таким образом, тело либо деформируется, либо перемещается в пространстве. Деформацию тел изучает наука – сопротивление материалов. Так как в теоретической механике имеют дело с абсолютно твёрдыми телами, то при механическом действии тела изменяют свое положение в пространстве относительно друг друга. В общем случае тело может поступательно перемещаться в пространстве по трём направлениям (параллельно координатным осям OX, OY, OZ) и вращаться относительно этих осей (рис. 1.2).

 

Свободное тело – тело, на перемещения которого в пространстве не наложено никаких ограничений.

 

Следовательно, свободное тело может осуществлять в системе отсчёта OXYZ шесть движений. Другими словами, тело имеет шесть степеней свободы.

Тело может находиться в состоянии покоя, которое является частным случаем механического движения, когда скорости точек рассматриваемого тела равны нулю. Если тело покоится, то говорят, что оно находится в состоянии равновесия.

 

Равновесие механической системы – состояние механической системы, при котором её точки под действием приложенных сил остаются в покое по отношению к рассматриваемой системе отсчёта.

Система отсчёта – система координат, связанная с телом, по отношению к которому определяется положение других тел (механических систем) в разные моменты времени.

 

Важнейшим понятием в теоретической механике является понятие силы.

 

Сила – векторная величина, являющаяся мерой механического действия одного тела на другое.

 

Сила как вектор определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Графически силу изображают направленным прямолинейным отрезком (вектором), совпадающим по направлению с направлением силы (рис. 1.3).

F

Длина этого отрезка выражает в выбранном масштабе модуль силы, его начало совпадает с точкой приложения силы. Иногда удобно изображать силу так, что точкой её приложения является конец вектора силы – острие стрелки. Силу и её модуль обозначают следующим образом: F, P, Q – сила; F, P, Q – модуль силы. В технической литературе используют и другой вид обозначения силы: , , .

 

Линия действия силы – прямая линия, вдоль которой направлен вектор, изображающий силу.

 

Простейшим примером силы является сила тяжести, с которой тело притягивается к Земле.

Сила тяжести – сила, действующая на материальную точку вблизи земной поверхности, равная произведению массы m этой точки на ускорение g свободного падения в вакууме.

G = m· g.

 

Сила тяжести G прикладывается в центре С тяжести тела и направлена к центру Земли (по вертикали). В неподвижной (НСО) относительно Земли системе отсчёта OXYZ сила тяжести тела изображается так, как это показано на рис. 1.4.

Если речь идет о величине (модуле) силы тяжести тела, то употребляют термин «вес тела».

 

Вес тела – сумма модулей сил тяжести, действующих на частицы этого тела.

 

Вес G тела находят по формуле

G = m·g.

Силы имеют различную физическую природу, например, сила давления пара, сила притяжения наэлектризованных тел и т. д. В теоретической механике не рассматривают физическую природу сил, здесь важны только величина, направление и точка приложения силы. Модуль силы измеряют в ньютонах [H].

Силы, действующие на механическую систему, делят на две группы: внешние и внутренние.

Внешняя сила – сила, действующая на какую-либо точку механической системы со стороны тел, не принадлежащих рассматриваемой механической системе.

 

Внешние силы принято обозначать символами: F _i^E, R _i^E.

 

Внутренние силы – силы, действующие на какие-либо точки механической системы со стороны других точек, принадлежащих рассматриваемой механической системе.

 

Внутренние силы принято обозначать символом R _i^J.

 

Система сил – любая совокупность сил, действующих на механическую систему.

 

Систему сил принято обозначать (F ₁,…, F _n).

Уравновешенная система сил – система сил, которая будучи приложена к свободному телу, находящемуся в равновесии, не выводит его из этого кинематического состояния.

Уравновешивающая система сил – система сил, которая вместе с заданной другой системой сил составляет уравновешенную систему сил.

Эквивалентные системы сил – две или несколько систем сил, имеющих одну и ту же уравновешивающую систему сил.

 

Эквивалентные системы сил приводят свободное тело в одно и то же кинематическое состояние. Для обозначения эквивалентности систем сил используют знак «~».

Равнодействующая системы сил – сила, эквивалентная данной системе сил.

Плоская система сил – система сил, линии действия которых расположены в одной плоскости.

Сходящаяся система сил – система сил, линии действия которых пересекаются в одной точке.

 

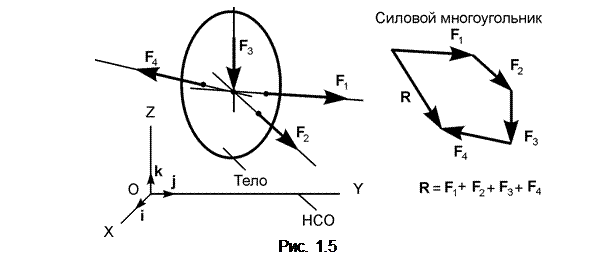
Из курса физики известно, что равнодействующая сходящейся системы сил графически определяется по правилу силового многоугольника (рис. 1.5).

При построении силового многоугольника равнодействующая R соединяет начало первого вектора с концом последнего. Силовой многоугольник не замкнут.

Таким образом, сходящаяся система сил имеет равнодействующую R, определяемую векторным равенством:

R = F ₁ +…+ F ₄.

В общем случае для системы сходящихся сил (F ₁,…, F _n) используют векторное равенство R = Σ F _i.

 

Уравновешенную систему сил графически изображают замкнутым силовым многоугольником, в котором конец последнего вектора приходит в начало первого вектора (рис. 1.6).

Такую систему сил описывают равенством R = F ₁ +…+ F ₄ = 0. В общем случае для уравновешенной системы сил (F ₁,…, F _n) справедливо равенство R = Σ F _i = 0.

Силы делят на сосредоточенные и распределённые.

Сосредоточенная сила – сила, приложенная к телу в какой-либо одной его точке.

Распределённые силы – силы, действующие на все точки некоторой части линии, поверхности или объёма.

 

Понятие о сосредоточенной силе является условным, так как практически приложить силу в точке нельзя. Силу, которую в механике рассматривают как сосредоточенную, представляет собой равнодействующую некоторой системы распределённых сил.

Распределённые силы характеризуются величиной q интенсивности распределения силы, т. е. величиной силы на единицу объёма, поверхности или длины линии. Интенсивность распределения силы может иметь следующие размерности: Н/м³; Н/м²; Н/м. На тела в основном действуют параллельные и сходящиеся распределённые силы. К параллельным силам, распределённым по объёму, относятся силы тяжести частиц тела.

Поскольку все аксиомы и теоремы статики формулируются для сосредоточенных сил, необходимо рассмотреть способы перехода от распределённых сил к сосредоточенным силам.

Рассмотрим замену линейно распределённых сил сосредоточенной силой.

Равнодействующую распределённых на линии параллельных сил постоянной интенсивности q определяют по формуле Q = q ×L, где L – длина балки (рис. 1.7).

Равнодействующая распределённых сил (сосредоточенная сила) прикладывается к балке под центром тяжести площади прямоугольника.

В инженерной практике часто применяют нагрузку, интенсивность которой изменяется по закону треугольника (рис. 1.8).

 

Равнодействующую параллельных распределённых сил на линии с интенсивностью, изменяющейся по закону треугольника, определяют по формуле Q = 0,5 q _max×L, где q _max – наибольшая интенсивность. Линия действия сосредоточенной силы Q смещена в сторону наибольшей интенсивности и проходит через центр тяжести площади треугольника.

В более сложных случаях распределённые нагрузки заменяют несколькими сосредоточенными силами. Пример такой замены приведен на рис. 1.9.

Модули Q₁, Q₂ сил Q ₁, Q ₂ определяют по формулам:

Q₁ = q₁·L; Q₂ = 0,5·(q₂ – q₁)·L.

Аксиомы статики

 

 

1. Аксиома инерции. Под действием уравновешенной системы сил (Σ F_i = 0 или ( F₁,…, F_n ) ~ 0) свободное тело находится в состоянии покоя или равномерного прямолинейного движения.

2.
Аксиома равновесия двух сил. Две силы, приложенные к телу, уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны (рис. 1.10).

3. Аксиома присоединения и исключения уравновешенной системы сил. Действие системы сил на тело не изменится, если к ней присоединить или из неё исключить уравновешенную систему сил.

Следствие 1

 

Не изменяя кинематического состояния тела, силу можно переносить по линии действия, сохраняя неизменными её модуль и направление (рис. 1.11).

Так как силу можно переносить в любую точку её линии действия, то силу рассматривают как скользящий вектор.

Следствие 2

 

Систему сходящихся сил можно заменить системой сил, приложенных в одной точке (рис. 1.12).

 

4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах (рис. 1.13).

Это положение выражается следующим геометрическим равенством: R = F ₁ + F ₂. Модуль равнодействующей силы определяют по формуле

,

где j – угол между направлениями сил F ₁ и F ₂.

Параллелограмм сил можно заменить силовым треугольником. Тогда справедливо равенство

.

Эта аксиома допускает и обратное утверждение. Силу можно разложить бесчисленным образом раз на две силы, параллельные выбранным произвольным координатным осям (рис. 1.14).

F = F _OX + F _OY = F _O1X1 + F _O1Y1.

 

Векторы F _OX, F _OY, F _O1X1, F _O1Y1 называют компонентами силы F по соответствующим координатным осям.

 

Примечание. Силу F раскладывают на составляющие по координатным осям только в точке её приложения.

5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.

 

Эта аксиома утверждает, что силы действия друг на друга двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

На рис. 1.15 груз А лежит на столе В. Груз весом G давит на стол. Сила давления груза на стол равна силе тяжести G. Стол же противодействует грузу с силой N.

Таким образом, в природе не существует одностороннего действия силы. Однако эти силы не образуют уравновешенную систему сил, так как они приложены к разным телам.

 

6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердевании. Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердевании.

 

Из этой аксиомы следует, что условия равновесия сил, приложенных к телу, должны выполняться и для сил, приложенных к деформирующемуся телу. Однако в случае деформирующегося тела эти условия необходимы, но недостаточны. Так, например, условие равновесия двух сил, приложенных к стержню на его концах, состоит в том, что силы равны по модулю и направлены по одной прямой в противоположные стороны. Две уравновешивающиеся силы, приложенные к нити, удовлетворяют этому условию, но при наличии дополнительного условия: силы должны только растягивать, а не сжимать нить.

 

Вопросы и задания для самоконтроля

 

 

1. Сформулировать определение термина «механика».

2. Сформулировать определение термина «теоретическая механика».

3. Сформулировать определение термина «статика».

4. Сформулировать определение термина «масса».

5. Сформулировать определение термина «инертность».

6. Сформулировать определение термина «материальная точка».

7. Сформулировать определение термина «абсолютно твёрдое тело».

8. Сформулировать определение термина «механическая система».

9. Сформулировать определение термина «механическое действие».

10. Сформулировать определение термина «механическое движение».

11. Сформулировать определение термина «свободное тело».

12. Сформулировать определение термина «равновесие механической системы».

13. Сформулировать определение термина «система отсчёта».

14. Сформулировать определение термина «сила».

15. Сформулировать определение термина «линия действия силы».

16. Сформулировать определение термина «сила тяжести».

17. Сформулировать определение термина «вес тела».

18. Сформулировать определение термина «внешняя сила».

19. Сформулировать определение термина «внутренние силы».

20. Сформулировать определение термина «система сил».

21. Сформулировать определение термина «уравновешенная система сил».

22. Сформулировать определение термина «уравновешивающая система сил».

23. Сформулировать определение термина «эквивалентные системы сил».

24. Сформулировать определение термина «равнодействующая системы сил».

25. Сформулировать определение термина «плоская система сил».

26. Сформулировать определение термина «сходящаяся система сил».

27. Сформулировать определение термина «сосредоточенная сила».

28. Сформулировать определение термина «распределённые силы».

29. Сформулировать аксиому инерции.

30. Сформулировать аксиому равновесия двух сил.

31. Сформулировать аксиому присоединения и исключения уравновешенной системы сил.

32. Сформулировать первое следствие из аксиомы присоединения и исключения уравновешенной системы сил.

33. Сформулировать второе следствие из аксиомы присоединения и исключения уравновешенной системы сил.

34. Сформулировать аксиому параллелограмма сил.

35. Сформулировать аксиому равенства действия и противодействия.

36. Сформулировать аксиому равновесия сил, приложенных к деформирующемуся телу при его затвердевании.

37. Записать формулу для определения равнодействующей системы сходящихся сил.

38. Записать формулу для определения модуля сосредоточенной силы при действии на балку распределённой нагрузки с интенсивностью q, изменяющейся по закону прямоугольника.

39. Записать формулу для определения модуля сосредоточенной силы при действии на балку распределённой нагрузки с интенсивностью q, изменяющейся по закону треугольника.

40. Используя аксиому параллелограмма сил, записать формулу для определения модуля равнодействующей двух сходящихся сил.

41. Используя правило треугольника, записать формулу, связывающую модули двух сходящихся сил и их равнодействующую.

42. Записать формулу, выражающую аксиому равновесия двух сил.

 

 

Связи и реакции связей

 

 

Несвободное тело – тело, на перемещения которого в пространстве наложены ограничения.

 

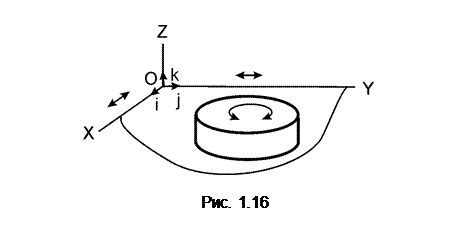
На рис. 1.16 изображено несвободное тело, лежащее на горизонтальной плоскости OXY. Эта плоскость наложила следующие ограничения на перемещения цилиндра: поступательное перемещение, параллельное оси OZ, и повороты относительно осей OX и OY. Плоскость OXY по отношению к телу является связью.

Связи – материальные тела, накладывающие ограничения на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах.

 

Плоскость OXY (см. рис. 1.16) позволяет цилиндру осуществлять поступательные движения, параллельные координатным осям OX и OY, и поворот в плоскости OXY. Пример несвободного тела – дверь, подвешенная на шарнирах. Связями для двери являются шарниры.

Тело А (рис. 1.17), стремясь под действием силы тяжести G осуществить вертикальное перемещение, которому препятствует связь (тело В), действует на него с некоторой силой, называемой силой давления на связь.

Одновременно (по аксиоме 5) связь действует на тело с такой же по модулю, но противоположно направленной силой N: N = – G. Силу N называют реакцией связи. Реакции связей относятся к разряду внешних сил.

Реакции связей – силы, действующие на точки механической системы со стороны материальных тел, осуществляющих связи, наложенные на эту систему.

 

В дальнейшем силы, не являющиеся реакциями связей, называют активными силами. Активные силы, как и реакции связей, относятся к разряду внешних сил. Особенностью активной силы является то, что её модуль и направление непосредственно не зависят от других, действующих на тело сил. Реакция связи зависит от действующих на тело активных сил и заранее неизвестна. Если на тело не действуют активные силы, то реакции связей равны нулю.

Для определения величин реакций связей надо решить соответствующую задачу статики. Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Если связь одновременно препятствует перемещениям тела по нескольким направлениям, то направление реакции связи заранее неизвестно и должно определяться при решении конкретной задачи.

Рассмотрим подробнее, как направлены реакции основных видов связей.

Гладкая связь – материальное тело, имеющее поверхность, силами трения о которую рассматриваемой механической системы пренебрегают.

 

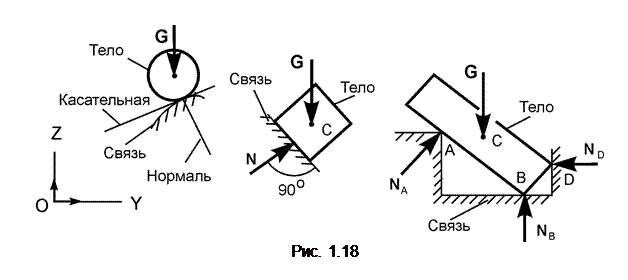
Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис. 1.18).

 

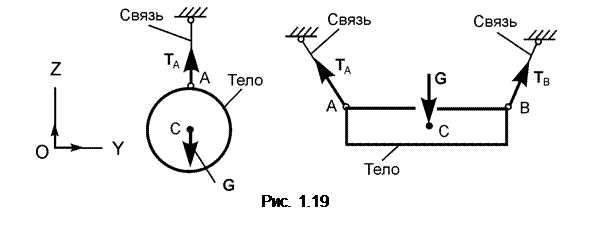
Реакция N гладкой поверхности направлена по общей нормали к поверхности соприкасающихся тел в точке их касания и приложена в этой точке со стороны связи.

Когда одна из соприкасающихся поверхностей является точкой или линией, то реакция этой связи направлена по нормали к другой поверхности. Зачастую реакцию N называют нормальной реакцией.

Гибкая связь – нерастяжимые нить или трос, вес которых не учитывают.

 

На рис. 1.19 изображены тела (механические системы), на которые наложены гибкие связи (нити).

Реакции Т _А, Т _В натянутых нитей направлены вдоль нитей от тела к точкам подвеса нитей.

Невесомый стержень – недеформируемый стержень, загруженный только по его концам.

 

Невесомый стержень соединяется с телом и опорой шарнирно. На рис. 1.20 изображена балка, опирающаяся на три невесомых стержня.

При этом один стержень прямой, а остальные изогнуты. Реакция невесомого стержня направлена по линии, соединяющей концы стержня. Прямой стержень работает только на растяжение или сжатие.