
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И абсолютного ускорения точки»Содержание книги
Поиск на нашем сайте
По заданным уравнениям относительного движения точки М и движения тела D определить для момента времени t1 абсолютные скорость и ускорение точки М. Схемы механизмов показаны на рисунках, а необходимые для расчёта данные приведены в табл. 2.4. Определить кинематические характеристики точки М в момент времени t1 (OM(t1) – положение точки на траектории относительного движения; V e(t1) – переносная скорость; V r(t1) – относительная скорость; V (t1) – абсолютная скорость; a r(t1) – относительное ускорение; a е(t1) – переносное ускорение; a с(t1) – ускорение Кориолиса; a (t1) – абсолютное ускорение). Для каждого варианта положение точки М на расчётной схеме соответствует положительному значению дуговой координаты ОМ = f(t). Таблица 2.4
Продолжение табл. 2.4
Продолжение табл. 2.4
Продолжение табл. 2.4
Продолжение табл. 2.4
Продолжение табл. 2.4
Продолжение табл. 2.4
Продолжение табл. 2.4
Окончание табл. 2.4
2.27. Пример выполнения курсового задания К 4
Дано: уравнение относительного движения точки М OM = Sr = Sr(t) = 2,5·p·t2, см; уравнение вращательного движения тела D φe = φe(t) = 2·t3 – 5·t, рад; t1 = 1 c; R = 40 см.
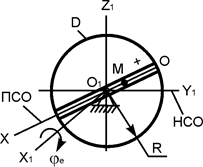
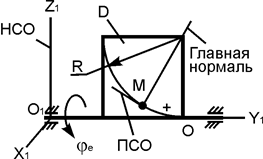
Решение. Точка М осуществляет сложное движение, поэтому для решения задачи необходимо ввести неподвижную систему отсчёта O1X1Y1Z1 и подвижную систему отсчёта OXYZ. Изобразим рассматриваемый механизм в момент времени t1 (рис. 2.50). Координатную ось O1Y1 неподвижной системы отсчёта направим по оси вращения тела D. Подвижную систему отсчёта OXYZ закрепим на теле D, расположив начало отсчёта в точке О. По исходным данным уравнение относительного движения точки М задано естественным способом Sr(t) = 2,5·p·t2. Исходя из этого, известны следующие характеристики движения: вид траектории движения – дуга окружности радиусом R; начало отсчёта дуговой координаты Sr – точка О; положительное направление отсчёта дуговой координаты Sr – знак (+); уравнение движения Sr = 2,5·p·t2.
Определим положение точки М на траектории относительного движения в момент времени t1: Sr(t1) = 2·p·(t1)2 = 2,5·p·22 = 10p см > 0. Для координации точки М на траектории относительного движения целесообразно использовать центральный угол: a(t1) = Sr(t1)/R = 2,5·p·(t1)2/R = 2,5·p·22/40 = p/4. Итак, α(t1) = 45о. Точка М тела D, совершающего вращательное движение в неподвижной системе отсчёта O1X1Y1Z1, описывает окружность радиусом MK = R – R·cos(α(t1)) = R·(1 – cos(α(t1))= 40·(1 – 0,707) = 11,72 см. Таким образом, траектория переносного движения точки М установлена. Это окружность радиусом МК с центром в точке К, расположенной на оси вращения тела D. Абсолютное движение точки М – это сумма относительного и переносного движений. Таким образом, траектория абсолютного движения точки М представляет собой винтовую линию, расположенную на сферическом конусе. Для определения абсолютной скорости V точки М используется векторное равенство V = V r + V e, где V r – вектор относительной скорости; V e – вектор переносной скорости. Определим проекцию
В момент времени t1 имеем
Поскольку Для определения переносной скорости V e предварительно найдем модуль ωе угловой скорости ωe = I В момент времени (t1) имеем ωe(t1) = I6·(t1)2 – 5I = I6·22 – 5I = 19 рад/c > 0. Поскольку ωe(t1) > 0, то величина угла φе возрастает. Покажем на рис. 2.50 направление вращения и определим модуль переносной скорости Ve(t1) по формуле Ve(t1) = ωe(t1)·МК = 19·11,72 = 222,68 см/с. Так как Ve(t1) направлена по касательной к траектории переносного движения, то она перпендикулярна плоскости OYZ подвижной системы отсчёта. С другой стороны, V r ┴ V e. Исходя из этого, определим модуль абсолютной скорости: V(t1) = Если V r не перпендикулярна V e, то определение модуля скорости V следует определять через проекции векторного выражения V = V r + V e на координатные оси неподвижной системы отсчёта O1X1Y1Z1.
где V(t1) = = = Для ориентации абсолютной скорости V в пространстве неподвижной системы отсчёта определим направляющие косинусы. cos(V, i 1) = cos(V, j 1) = cos(V, k 1) = При определении абсолютного ускорения a точки М используется формула a = a r+ a e+ a c, где a r – относительное ускорение; a e – переносное ускорение; a c – ускорение Кориолиса. Поскольку относительное движение задано естественным способом, то справедливо равенство a r = где Так как переносное движение является вращательным, то переносное ускорение a e находят по формуле a e= где Исходную формулу для определения абсолютного ускорения можно представить в следующем виде: a = Приступаем к определению слагаемых в правой части последнего выражения.
Так как
Вектор Модуль a r(t1) относительного ускорения a r(t1) в момент времени t1 определим по формуле a r(t1) = = Модуль
Вектор Для определения переносного вращательного ускорения εe = I εe(t1) = 12·t1 = 12·2 = 24 рад/с2. Так как
Покажем вектор Модуль a e(t1) переносного ускорения a е(t1) в момент времени t1 определим по формуле a е(t1) = = Приступаем к определению модуля ускорения Кориолиса. a c(t1) = 2ωе(t1)·Vr(t1)·sin( Согласно определению вектор a c(t1) = 2ωе(t1)·Vr(t1)·sin( = 2·19·31,4·0,707 = 843,59 см/с2. По правилу векторного произведения (a c = 2( Таким образом, в векторном равенстве a = известны все слагаемые, находящиеся в его правой части. Определим модуль a (t1) абсолютного ускорения a (t1) через его проекции
= – 15,7·0,707 + 24,64·0,707 = 6,32 см/с2;
= 15,7·0,707 + 24,64·0,707 – 4230,92 = – 4202,39 см/с2; a (t1) = Для ориентации абсолютного ускорения в пространстве определим направляющие косинусы. cos(a, i 1) = cos(a, j 1) = cos(a, k 1) = Результаты расчётов сводятся в таблицу. Таблица
Кинематические характеристики точки М в момент времени t1
Окончание таблицы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.24 (0.007 с.) |



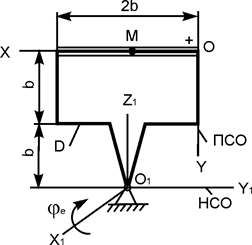




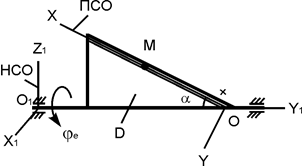

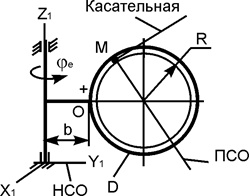




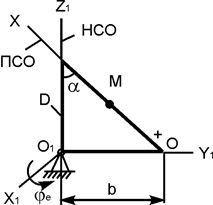
 ·(t2 + t), см;
φe = 0,2·t3 + t; рад;
t1 = 2 c;
b = 60 см;
α = 45o
·(t2 + t), см;
φe = 0,2·t3 + t; рад;
t1 = 2 c;
b = 60 см;
α = 45o


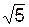 см;
t1 = 1 c
см;
t1 = 1 c













 относительной скорости V r на касательную:
относительной скорости V r на касательную: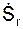 = 5·p·t.
= 5·p·t.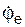 переносного вращения.
переносного вращения. =
=  = 224,88 см/с.
= 224,88 см/с. = Ve;
= Ve;  = – Vr·cos(α);
= – Vr·cos(α);  = Vr·sin(α),
= Vr·sin(α), =
= =
= = 224,88 см/с.
= 224,88 см/с. +
+ 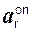 ,
, +
+  ,
, =
=  = d
= d  (t1)= (Vr(t1))2/ρ = (Vr(t1))2/R = (3,14)2/40 = 24,64 см/с2.
(t1)= (Vr(t1))2/ρ = (Vr(t1))2/R = (3,14)2/40 = 24,64 см/с2. =
= = 29,276 cм/c2.
= 29,276 cм/c2. (t1) переносного центростремительного ускорения
(t1) переносного центростремительного ускорения  .
. (t1) = εe(t1)·МК = 24·11,72 = 281,28 см/с2.
(t1) = εe(t1)·МК = 24·11,72 = 281,28 см/с2. =
= = 4240,259 cм/c2.
= 4240,259 cм/c2. (t1), V r(t1)).
(t1), V r(t1)).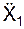 (t1),
(t1), 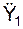 (t1),
(t1),  (t1) на оси неподвижной системы отсчёта O1X1Y1Z1 в момент времени (t1).
(t1) на оси неподвижной системы отсчёта O1X1Y1Z1 в момент времени (t1). = 4350,01 см/с2.
= 4350,01 см/с2. (t1),
см/с2
(t1),
см/с2
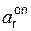 (t1),
см/с2
(t1),
см/с2
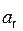 (t1),
см/с2
(t1),
см/с2
 , см/с2
, см/с2
 , см/с2
, см/с2
 , см/с2
, см/с2



