
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитический способ сложения силСодержание книги
Поиск на нашем сайте
Проекция равнодействующей сходящейся системы сил на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Пусть на тело действует система сил (F 1,…, F 4), при этом линии действия сил расположены в плоскости OXY (рис. 1.30).
Их равнодействующая R = F 1 + … + F 4. Спроецируем составляющие векторы и их равнодействующую на ось OX. Очевидно F1OX > 0, F2OX > 0, F3OX > 0, F4OX < 0, ROX > 0. Из рис. 1.30 видно, что ROX = F1OX + F2OX + F3OX + F4OX. Для любой сходящейся системы сил (F 1,…, F n), обозначая их равнодействующую через R, получим: ROX = Σ FiOX; ROY = Σ FiOY; ROZ = Σ FiOZ. Зная проекции ROX, ROY, ROZ равнодействующей R на координатные оси, можно найти её модуль и направляющие косинусы.
cos(R, i) = ROX/R; cos(R, j) = ROY/R; cos(R, k) = ROZ/R.
Для плоской сходящейся системы сил последние выражения приобретают вид: ROX = Σ FiОX; ROY = Σ FiОY;
cos(R, i) = ROX/R; cos(R, j) = ROY/R. Известно, что сходящаяся система сил уравновешивается только в том случае, если их равнодействующая равна нулю. Графически плоская сходящаяся система сил изображается замкнутым силовым многоугольником (рис. 1.31).
В общем случае R = Σ F i = 0. В замкнутом силовом многоугольнике все силы направлены в одну сторону по обходу многоугольника. Частный случай. Три сходящиеся силы уравновешиваются, если треугольник этих сил замкнут.
Геометрическое условие равновесия сходящейся системы сил, расположенных в пространстве и на плоскости, одно и то же. Однако графический метод решения задач на равновесие сходящейся системы сил практически применяется только для плоской системы сходящихся сил. Аналитические условия равновесия Системы сходящихся сил
В случае если силы взаимно уравновешиваются, их равнодействующая равна нулю. Аналитически это выражается соответствующими уравнениями равновесия. Для пространственной системысходящихся сил уравнения равновесия имеют вид: Σ FiOX = 0; Σ FiOY = 0; Σ FiOZ = 0. Для плоской сходящейся системы сил уравнения равновесия приводятся к виду: Σ FiOX = 0; Σ FiOY = 0. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей системы отсчёта равнялись нулю.
При помощи этих уравнений можно решить задачи на равновесие сходящейся системы сил на плоскости и в пространстве.
Алгоритм решения задач статики
Как правило, в задачах статики по известным активным силам F iE требуется определить реакции R iE внешних связей, наложенных на механическую систему. Напомним, что активные силы и реакции связей относятся к разряду внешних сил. С учётом этого геометрическое условие равновесия внешних сил записывают в следующем виде Σ F iE + Σ R iE = 0.
Для равновесия механической системы необходимо и достаточно, чтобы геометрическая сумма активных сил FiE и реакций внешних связей RiE, приложенных к этой системе, равнялась нулю.
При такой системе обозначений внешних сил аналитические условия равновесия пространственной сходящейся системы сил выражаются тремя уравнениями: Σ Σ Σ Для равновесия механической системы, на которую наложены внешние связи, необходимо и достаточно, чтобы суммы проекций активных сил FiE и реакций внешних связей RiE на координатные оси системы отсчёта равнялись нулю.
Для плоской сходящейся системы сил имеем два уравнения: Σ Σ
Все задачи на равновесие внешних сил, приложенных к телу, решаются по следующему алгоритму.
Алгоритм решения задач статики
1. Выбирают систему отсчёта. 2. Выбирают тело, к которому приложена система уравновешивающихся сил. 3. Показывают все действующие на тело активные нагрузки. 4. Согласно аксиоме связей действие связей на тело заменяют соответствующими реакциями связей. 5. К полученной системе сил применяют уравнения равновесия, соответствующие этой системе сил. 6. Из уравнений равновесия определяют неизвестные величины. Пример решения задачи
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.94.112 (0.006 с.) |


 =
=  ;
; =
=  ;
;

 + Σ
+ Σ  = 0;
= 0;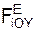 + Σ
+ Σ 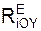 = 0;
= 0;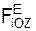 + Σ
+ Σ 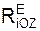 = 0.
= 0.


