
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоской произвольной системы силСодержание книги
Поиск на нашем сайте
Плоская произвольная система сил – система сил, линии действия которых произвольно расположены в одной плоскости.
Линии действия плоской произвольной системы сил пересекаются в различных точках.
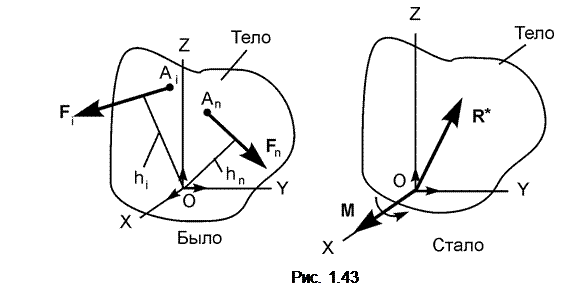
Последовательно применяя метод Пуансо для каждой из сил F i, осуществим параллельный перенос сил из точек Ai в начало О системы отсчёта OXYZ. Согласно этому методу, сила F iбудет эквивалентна силе F i,приложенной в точке О, и присоединённой паре сил с моментом M i = M О(F i ). При этом Mi = ± Fi×hi, где hi – плечо силы F i относительно центра приведения О. По окончании этой работы получим сходящуюся систему сил (F i,…, F n) и сходящуюся систему векторных моментов M i = M О(F i) присоединённых пар сил, приложенных в центре приведения. Сложив векторы сил, получим глав ный вектор R * = Σ F i и главный момент эквивалентной пары сил M = Σ M О(F i). Таким образом, плоская произвольная система сил (Fi,…, Fn) эквивалентна одной силе R* = Σ Fi и паре сил с моментом M = Σ MО(Fi). При решении задач статики используют проекции силы на координатные оси и алгебраические моменты сил относительно точки. На рис. 1.44 изображена плоская произвольная система сил, приведённая к главному вектору сил, модуль которой R*=
В этих формулах Σ FiОX, Σ FiОY – суммы проекций сил на координатные оси; Σ MО(F i) – сумма алгебраических моментов сил относительно точки О. Геометрическое условие равновесия любой системы сил выражается векторными равенствами: R * = Σ F i= 0; M = Σ M О(F i) = 0. При решении задач требуется определить реакции R iE внешних связей, наложенных на механическую систему. При этом активные силы F iE, приложенные к этой системе, известны. Так как активные силы F iE и реакции связей R iE относятся к разряду внешних сил, то геометрическое условие равновесия системы внешних сил целесообразно выразить векторными равенствами:
Σ F iE + Σ R iE = 0; Σ M A(F iE) + Σ M A(R iE) = 0.
Для равновесия системы внешних сил необходимо и достаточно, чтобы геометрическая сумма активных сил FiE и реакций RiE внешних связей и геометрическая сумма моментов активных сил MA(FiE) и реакций внешних связей MA(RiE) относительно произвольной точки А равнялись нулю.
Проецируя эти векторные равенства на координатные оси системы отсчёта, получим аналитические условия равновесия системы внешних сил. Для плоской произвольной системы сил эти уравнения приобретают следующий вид: Σ Σ Σ MA(F iE) + Σ MA(R iE) = 0, где Σ Совокупность этих формул есть первая (основная) форма уравнений равновесия плоской произвольной системы внешних сил. Таким образом, для равновесия плоской произвольной системы внешних сил, приложенных к механической системе, необходимо и достаточно, чтобы суммы проекций активных сил и реакций внешних связей на две координатные оси и сумма алгебраических моментов активных сил и реакций внешних связей относительно произвольной точки А равнялись нулю.
Существуют и другие формы уравнений равновесия плоской произвольной системы сил. Вторая форма выражается совокупностью формул: Σ Σ MA(F iE) + Σ MA(R iE) = 0; Σ MВ(F iE) + Σ MВ(R iE) = 0. Для равновесия плоской произвольной системы внешних сил, приложенных к телу, необходимо и достаточно, чтобы сумма проекций сил на координатную ось и суммы алгебраических моментов сил относительно произвольных точек А и В равнялись нулю. Третья форма уравнений равновесия выражается совокупностью формул: Σ MA(F iE) + Σ MA(R iE) = 0; Σ MВ(F iE) + Σ MВ(R iE) = 0; Σ MС(F iE) + Σ MС(R iE) = 0. Для равновесия плоской произвольной системы внешних сил, приложенных к телу, необходимо и достаточно, чтобы суммы алгебраических моментов этих сил относительно произвольных точек А, В и С равнялись нулю.
При использовании третьей формы уравнений равновесия точки А, В и С не должны лежать на одной прямой.
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.006 с.) |

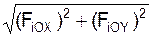 и эквивалентной паре сил с алгебраическим моментом M = Σ MО(F i).
и эквивалентной паре сил с алгебраическим моментом M = Σ MО(F i).
 + Σ
+ Σ  = 0;
= 0;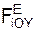 + Σ
+ Σ 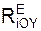 = 0;
= 0;


