
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устранение избыточных связейСодержание книги
Поиск на нашем сайте
Если определение числа избыточных связей – это анализ, то их устранение – это синтез. Исходя из главного условия синтеза – отсутствия избыточных связей, в структурную формулу подставляют
Найденное Выбрав один из вариантов раскладки связей, строят механизм. Подставляя пары, следят за тем, чтобы механизм получился кинематически эквивалентным исходному и имел во всех своих положениях (фазах движения) заданное число степеней свободы. Подобрать и сориентировать пары с выбранными числами связей помогает воображаемая неточность изготовления или деформация стойки: пары ориентируют так, чтобы все вместе они допускали любые её деформации (как в примере на рис. 2.5, б). Пример. Требуется построить все структурные варианты кривошипно-ползунного механизма (рис. 2.4, а), удовлетворяющего условиям: Число кинематических пар – 4. Семнадцать связей раскладываются по четырём кинематическим парам в следующих трёх вариантах: 5+5+5+2; 5+5+4+3; 5+4+4+4. Все другие варианты являются перестановками найденных и реализуются в процессе построения схемы. Согласно первому варианту, одна из пар должна быть двусвязной. Двусвязными являются пары «цилиндр – плоскость» и «шар – цилиндр» (см. табл. 2.1). Подстановка пары «цилиндр – плоскость» взамен какой-либо вращательной пары, например 1-2, возможна в нескольких вариантах, отличающихся ориентацией пары. Два из этих вариантов приведены на рис. 2.6, а, б. Полученные механизмы не удовлетворяют условиям синтеза, т. к. появляется вторая степень свободы – z3 и j23 соответственно. Подстановка пары «цилиндр – плоскость» взамен поступательной пары 3-4 возможна также в нескольких вариантах, два из них приведены на рис. 2.6, в, г. В варианте в) цепь 0... 3 не позволяет звену 3 последовать за направляющей 4, если по каким-то причинам она будет развёрнута вокруг оси, параллельной z. В то же время эта цепь допускает вращение звена 3 вокруг оси y (см. угол j3). Это вращение означает появление второй степени свободы, что противоречит условиям синтеза. Рис. 2.6. Варианты подстановки пары «цилиндр – плоскость» Вариант г) допускает любые перемещения направляющей 4 и, значит, избыточных связей нет. Кроме того, исчезла вторая степень свободы. Таким образом, все условия синтеза удовлетворены. Приведённых примеров достаточно, чтобы оценить возможности пары «цилиндр – плоскость». Подстановка пары «шар – цилиндр» возможна также в нескольких вариантах. Один из правильных вариантов показан на рис. 2.5, б. Возможности алгебраического синтеза значительно расширяются, если допустить другое число степеней свободы – за счёт местных подвижностей, а также другое число звеньев – за счёт их разрезания с последующим подвижным соединением частей. Двумерные модели механизма Структуру и кинематику любого плоского механизма можно изучать как по трёхмерной, так и двумерной модели. На рис. 2.7 представлены трёхмерные – а, в и соответствующие двумерные – б, г модели плоских механизмов. Двумерная модель проще трёхмерной, и в этом её преимущество. Деление пар на высшие и низшие производится по трёхмерной модели. Класс, присвоенный при этом, сохраняется и при переходе к двумерной модели. Таким образом, на рис. 2.7, г пара 1 - 2 по-прежнему высшая, остальные низшие.
Рис. 2.7. Трёхмерные – а, в и соответствующие Связи пар двумерных моделей. Как и в трёхмерных моделях, связи пар двумерных моделей делятся на активные и пассивные. Принцип определения числа активных связей остаётся прежним. В кулачковой паре 1 - 2 (см. рис. 2.7, г) связь одна.
Рис. 2.8. Активные связи вращательной и поступательнойпар Структурная формула. Формула выводится так же, как для трёхмерных моделей, но отличается коэффициентом при числе подвижных звеньев
Отличие объясняется тем, что после удаления всех связей каждое подвижное звено остаётся в своём двумерном пространстве и обретает не шесть степеней свободы, а три, как всякая плоская фигура на плоскости (см. рис. 2.1). Из (2.3) выводят формулу числа избыточных связей:
В модели четырёхзвенника (рис. 2.7, б)
Рис. 2.9. Механизмы, двумерные модели которых Вычисления по формуле (2.4), выполненные в порядке следования механизмов на рисунке, дают следующие результаты:
Устранение избыточной связи, обнаруженной в каждом из трёх рассмотренных случаев, является сложным делом и в задачу данного курса не входит. Использование структурной формулы на этом не заканчивается: она применяется ещё и при кинематическом анализе.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.239.25 (0.008 с.) |

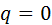 . Затем задаются величинами
. Затем задаются величинами 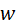 и
и 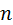 . Для упрощения задачи их принимают сначала такими, как в исходном механизме. Через принятые значения находят необходимое число связей
. Для упрощения задачи их принимают сначала такими, как в исходном механизме. Через принятые значения находят необходимое число связей
 раскладывают всеми возможными отличающимися по составу способами по кинематическим парам синтезируемого механизма. При раскладке учитывают, что в каждой кинематической паре содержится не более пяти активных связей (см. табл. 2.1).
раскладывают всеми возможными отличающимися по составу способами по кинематическим парам синтезируемого механизма. При раскладке учитывают, что в каждой кинематической паре содержится не более пяти активных связей (см. табл. 2.1).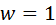 ,
,  . При этих условиях необходимое число связей
. При этих условиях необходимое число связей 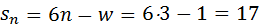 .
.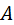 и
и  (рис. 2.8), следовательно, активных связей – по две.
(рис. 2.8), следовательно, активных связей – по две.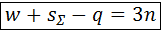 . (2.3)
. (2.3)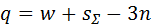 . (2.4)
. (2.4) ;
; 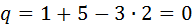 . Вообще, в двумерных моделях избыточные связи встречаются редко. Немногочисленные исключения приведены на рис. 2.9.
. Вообще, в двумерных моделях избыточные связи встречаются редко. Немногочисленные исключения приведены на рис. 2.9. ;
; 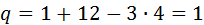 ;
; 


